Teoria wykresów - łączność
To, czy możliwe jest przejście grafu z jednego wierzchołka do drugiego, zależy od tego, w jaki sposób graf jest połączony. Łączność to podstawowa koncepcja w teorii grafów. Łączność określa, czy wykres jest połączony, czy odłączony. Zawiera podtematy oparte na krawędzi i wierzchołku, znane jako łączność krawędzi i łączność wierzchołków. Omówmy je szczegółowo.
Łączność
Mówi się, że jest to wykres connected if there is a path between every pair of vertex. Od każdego wierzchołka do każdego innego wierzchołka powinna istnieć jakaś ścieżka do przejścia. Nazywa się to łącznością wykresu. Mówi się, że graf z wieloma rozłączonymi wierzchołkami i krawędziami jest rozłączony.
Example 1
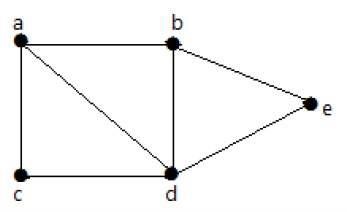
Na poniższym wykresie możliwe jest przejście od jednego wierzchołka do dowolnego innego wierzchołka. Na przykład, można przejść od wierzchołka „a” do wierzchołka „e”, używając ścieżki „ab-e”.
Example 2
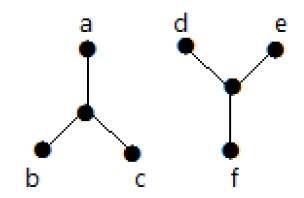
W poniższym przykładzie przejście od wierzchołka „a” do wierzchołka „f” nie jest możliwe, ponieważ nie ma między nimi bezpośredniej lub pośredniej ścieżki. Stąd jest to odłączony wykres.
Wytnij wierzchołek
Niech „G” będzie grafem połączonym. Wierzchołek V ∈ G nazywany jest wierzchołkiem ciętym „G”, jeśli „G-V” (Usuń „V” z „G”) skutkuje rozłączonym wykresem. Usunięcie wyciętego wierzchołka z wykresu dzieli go na dwa lub więcej wykresów.
Note - Usunięcie przeciętego wierzchołka może spowodować odłączenie wykresu.
Połączony graf „G” może mieć najwyżej (n – 2) przecięte wierzchołki.
Example
Na poniższym wykresie wierzchołki „e” i „c” to przecięte wierzchołki.

Po usunięciu „e” lub „c” wykres stanie się wykresem odłączonym.

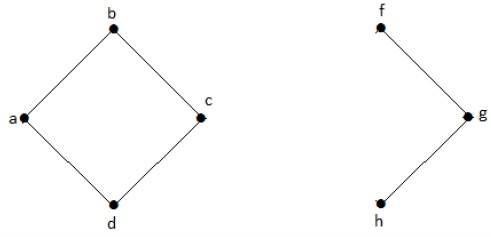
Bez „g” nie ma ścieżki między wierzchołkiem „c” a wierzchołkiem „h” i wieloma innymi. Stąd jest to odłączony graf z przeciętym wierzchołkiem jako „e”. Podobnie „c” jest również wyciętym wierzchołkiem dla powyższego wykresu.
Cut Edge (Bridge)
Niech „G” będzie grafem połączonym. Krawędź „e” ∈ G nazywana jest krawędzią tnącą, jeśli „G-e” daje w wyniku odłączony wykres.
Jeśli usunięcie krawędzi z wykresu prowadzi do dwóch lub więcej wykresów, wówczas ta krawędź nazywana jest krawędzią ciętą.
Example
Na poniższym wykresie krawędź cięcia to [(c, e)].

Usuwając krawędź (c, e) z wykresu, staje się on odłączonym wykresem.


Na powyższym wykresie usunięcie krawędzi (c, e) dzieli wykres na dwie części, co jest niczym innym jak odłączonym wykresem. Stąd krawędź (c, e) jest ciętą krawędzią wykresu.
Note - Niech więc „G” będzie grafem połączonym z „n” wierzchołkami
krawędź cięcia e ∈ G wtedy i tylko wtedy, gdy krawędź „e” nie jest częścią żadnego cyklu w G.
maksymalna możliwa liczba krawędzi ciętych wynosi „n-1”.
zawsze, gdy istnieją krawędzie cięte, istnieją również wierzchołki cięte, ponieważ co najmniej jeden wierzchołek krawędzi cięcia jest wierzchołkiem ciętym.
jeśli przecięty wierzchołek istnieje, wówczas krawędź cięcia może istnieć lub nie.
Wytnij zestaw wykresu
Niech „G” = (V, E) będzie grafem połączonym. Podzbiór E 'z E jest nazywany zbiorem ciętym G, jeśli usunięcie wszystkich krawędzi E' z G powoduje odłączenie G.
Jeśli usunięcie pewnej liczby krawędzi z wykresu powoduje jego rozłączenie, wówczas te usunięte krawędzie nazywane są zbiorem cięć wykresu.
Example
Spójrz na poniższy wykres. Jego zestaw cięć to E1 = {e1, e3, e5, e8}.
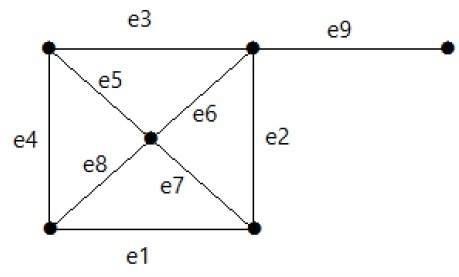
Po usunięciu zbioru cięć E1 z wykresu wyglądałoby to następująco -
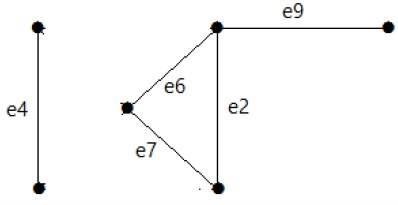
Podobnie istnieją inne zestawy cięć, które mogą odłączyć wykres -
E3 = {e9} - Najmniejszy wycięty zbiór wykresu.
E4 = {e3, e4, e5}
Edge Connectivity
Niech „G” będzie grafem połączonym. Minimalna liczba krawędzi, których usunięcie powoduje rozłączenie „G”, nazywana jest łącznością krawędzi G.
Notation - λ (G)
Innymi słowy, plik number of edges in a smallest cut set of G nazywana jest łącznością brzegową G.
Jeśli „G” ma obciętą krawędź, to λ (G) wynosi 1. (łączność krawędzi G.)
Example
Spójrz na poniższy wykres. Po usunięciu dwóch minimalnych krawędzi połączony wykres zostaje rozłączony. Stąd jego łączność krawędziowa (λ (G)) wynosi 2.
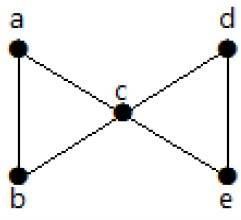
Oto cztery sposoby odłączenia wykresu przez usunięcie dwóch krawędzi -

Łączność Vertex
Niech „G” będzie grafem połączonym. Minimalna liczba wierzchołków, których usunięcie powoduje odłączenie „G” lub zredukowanie „G” do trywialnego grafu, nazywa się jego łącznością wierzchołków.
Notation - K (G)
Example
Na powyższym wykresie usunięcie wierzchołków „e” i „i” powoduje odłączenie wykresu.

Jeśli G ma przecięty wierzchołek, to K (G) = 1.
Notation - dla dowolnego połączonego wykresu G,
K (G) ≤ λ (G) ≤ δ (G)
Łączność wierzchołków (K (G)), łączność krawędzi (λ (G)), minimalna liczba stopni G (δ (G)).
Example
Obliczyć λ (G) i K (G) dla następującego wykresu -
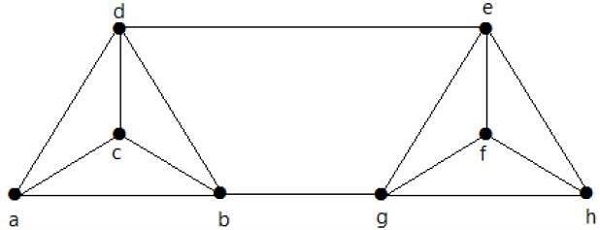
Solution
Z wykresu
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Usuwając krawędzie {d, e} i {b, h}, możemy odłączyć G.
W związku z tym,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
Z (2) i (3), łączność wierzchołków K (G) = 2