Teoria grafów - pokrycia

Graf pokrywający to podgraf zawierający albo wszystkie wierzchołki, albo wszystkie krawędzie odpowiadające innemu grafowi. Podgraf zawierający wszystkie wierzchołki nazywa się aline/edge covering. Podgraf, który zawiera wszystkie krawędzie, nazywa się avertex covering.

Pokrycie linii

Niech G = (V, E) będzie wykresem. Podzbiór C (E) nazywany jest pokryciem linii G, jeśli każdy wierzchołek G przypada na co najmniej jedną krawędź w C, tj.

deg (V) ≥ 1 ∀ V ∈ G

ponieważ każdy wierzchołek jest połączony z innym wierzchołkiem krawędzią. W związku z tym ma minimalny stopień 1.

Example

Spójrz na poniższy wykres -

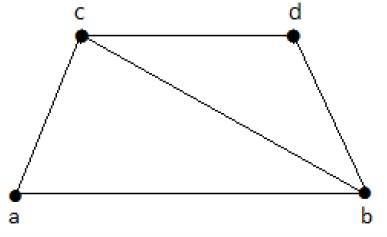
Jego podgrafy mające pokrycie linii są następujące:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Pokrycie linii „G” nie istnieje wtedy i tylko wtedy, gdy „G” ma izolowany wierzchołek. Pokrycie linii wykresu z „n” wierzchołkami ma co najmniej [n / 2] krawędzi.

Minimalne pokrycie linii

Mówi się, że linia pokrywająca C wykresu G jest minimalna if no edge can be deleted from C.

Example

Na powyższym wykresie podgrafy z pokryciem linii są następujące -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Tutaj C ₁ , C ₂ , C ₃ to minimalne pokrycia linii, podczas gdy C ₄ nie jest, ponieważ możemy usunąć {b, c}.

Minimalne pokrycie linii

Jest również znany jako Smallest Minimal Line Covering. Minimalne pokrycie linii z minimalną liczbą krawędzi nazywa się minimalnym pokryciem linii „G”. Liczba krawędzi w minimalnym pokryciu linii w „G” nazywana jestline covering number„G” (α ₁ ).

Example

W powyższym przykładzie C ₁ i C ₂ to minimalne pokrycie linii G i α ₁ = 2.

Każde pokrycie linii zawiera minimalne pokrycie linii.
Każde pokrycie linii nie zawiera minimalnego pokrycia linii (C ₃ nie zawiera żadnego minimalnego pokrycia linii.
Brak minimalnego pokrycia linii zawiera cykl.
Jeśli linia obejmująca „C” nie zawiera ścieżek o długości 3 lub więcej, to „C” jest minimalnym pokryciem linii, ponieważ wszystkie składowe „C” są gwiazdami, a z gwiezdnego grafu nie można usunąć żadnej krawędzi.

Pokrycie wierzchołków

Niech „G” = (V, E) będzie wykresem. Podzbiór K z V nazywany jest pokryciem wierzchołka „G”, jeśli każda krawędź „G” styka się z wierzchołkiem w „K” lub jest przez nie pokryta.

Example

Spójrz na poniższy wykres -

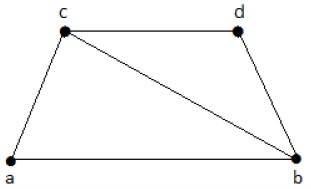
Podgrafy, które można wyprowadzić z powyższego wykresu, są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

Tutaj K ₁ , K ₂ i K ₃ mają pokrycie wierzchołków, podczas gdy K ₄ nie ma żadnego pokrycia wierzchołków, ponieważ nie zakrywa krawędzi {bc}.

Minimalne pokrycie wierzchołków

Mówi się, że wierzchołek „K” wykresu „G” stanowi minimalne pokrycie wierzchołków, jeśli żaden wierzchołek nie może zostać usunięty z „K”.

Example

Na powyższym wykresie podgrafy mające pokrycie wierzchołków są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Tutaj K ₁ i K ₂ są minimalnymi pokryciami wierzchołków, podczas gdy w K ₃ wierzchołek „d” można usunąć.

Minimalne pokrycie wierzchołków

Jest również znany jako najmniejsze minimalne pokrycie wierzchołków. Minimalne pokrycie wierzchołków grafu „G” przy minimalnej liczbie wierzchołków nazywane jest minimalnym pokryciem wierzchołków.

Liczba wierzchołków w minimalnym pokryciu wierzchołków „G” jest nazywana liczbą obejmującą wierzchołki G (α ₂ ).

Example

Na poniższym wykresie podgrafy mające pokrycie wierzchołków są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}