Teoria wykresów - szybki przewodnik

W dziedzinie matematyki i informatyki teoria grafów to nauka o grafach, która dotyczy relacji między krawędziami i wierzchołkami . Jest to popularny przedmiot mający swoje zastosowania w informatyce, informatyce, naukach biologicznych, matematyce i językoznawstwie, by wymienić tylko kilka. Bez zbędnych ceregieli zacznijmy od zdefiniowania wykresu.

Co to jest wykres?

Wykres jest obrazowym przedstawieniem zbioru obiektów, w którym niektóre pary obiektów są połączone linkami. Połączone obiekty są reprezentowane przez punkty określane jakovertices, a łącza łączące wierzchołki są nazywane edges.

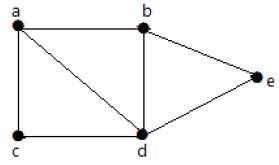
Formalnie wykres jest parą zbiorów (V, E), gdzie Vjest zbiorem wierzchołków, a E jest zbiorem krawędzi, łączących pary wierzchołków. Spójrz na poniższy wykres -

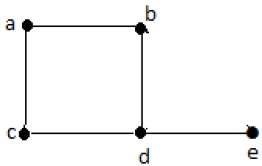
Na powyższym wykresie

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Zastosowania teorii grafów

Teoria grafów ma swoje zastosowania w różnych dziedzinach inżynierii -

Electrical Engineering- Pojęcia teorii grafów są szeroko stosowane w projektowaniu połączeń obwodów. Typy lub organizacja połączeń nazywane są topologiami. Niektóre przykłady topologii to topologie gwiazdy, mostka, szeregowe i równoległe.

Computer Science- Teoria grafów służy do badania algorytmów. Na przykład,

• Algorytm Kruskala
• Algorytm Prima
• Algorytm Dijkstry

Computer Network - Relacje między połączonymi komputerami w sieci są zgodne z zasadami teorii grafów.

Science - Strukturę molekularną i strukturę chemiczną substancji, strukturę DNA organizmu itp. Przedstawiają wykresy.

Linguistics - Drzewo parsowania języka i gramatyki języka wykorzystuje wykresy.

General- Trasy między miastami można przedstawić za pomocą wykresów. Przedstawienie hierarchicznie uporządkowanych informacji, takich jak drzewo genealogiczne, może być użyte jako specjalny typ wykresu zwany drzewem.

Wykres to diagram punktów i linii połączonych z punktami. Ma co najmniej jedną linię łączącą zestaw dwóch wierzchołków bez żadnego łączącego się wierzchołka. Pojęcie grafów w teorii grafów opiera się na kilku podstawowych terminach, takich jak punkt, linia, wierzchołek, krawędź, stopień wierzchołków, właściwości grafów, itp. W tym rozdziale omówimy te podstawy teorii grafów.

Punkt

A pointjest określoną pozycją w jednowymiarowej, dwuwymiarowej lub trójwymiarowej przestrzeni. Dla lepszego zrozumienia punkt można oznaczyć alfabetem. Można to przedstawić za pomocą kropki.

Przykład

Tutaj kropka to punkt o nazwie „a”.

Linia

ZA Lineto połączenie między dwoma punktami. Można to przedstawić za pomocą linii ciągłej.

Example

Tutaj „a” i „b” to punkty. Połączenie między tymi dwoma punktami nazywa się linią.

Wierzchołek

Wierzchołek to punkt, w którym spotyka się wiele linii. Nazywa się to również anode. Podobnie jak punkty, wierzchołek jest również oznaczany alfabetem.

Example

Tutaj wierzchołek jest nazywany alfabetem „a”.

Brzeg

Krawędź to matematyczny termin oznaczający linię, która łączy dwa wierzchołki. Z jednego wierzchołka można utworzyć wiele krawędzi. Bez wierzchołka nie można utworzyć krawędzi. Dla krawędzi musi istnieć wierzchołek początkowy i końcowy.

Example

Tutaj „a” i „b” to dwa wierzchołki, a połączenie między nimi nazywa się krawędzią.

Wykres

Graf „G” definiuje się jako G = (V, E), gdzie V jest zbiorem wszystkich wierzchołków, a E jest zbiorem wszystkich krawędzi wykresu.

Example 1

W powyższym przykładzie ab, ac, cd i bd to krawędzie wykresu. Podobnie a, b, c i d są wierzchołkami wykresu.

Example 2

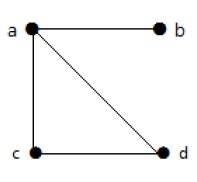
Na tym wykresie są cztery wierzchołki a, b, c i d oraz cztery krawędzie ab, ac, ad i cd.

Pętla

Na wykresie, jeśli krawędź jest rysowana od wierzchołka do siebie, nazywa się to pętlą.

Example 1

Na powyższym wykresie V jest wierzchołkiem, którego krawędź (V, V) tworzy pętlę.

Example 2

Na tym wykresie są dwie pętle utworzone w wierzchołku a i wierzchołku b.

Stopień wierzchołka

Jest to liczba wierzchołków sąsiadujących z wierzchołkiem V.

Notation - deg (V).

Na prostym grafie z liczbą n wierzchołków stopień dowolnych wierzchołków wynosi -

deg (v) ≤ n - 1 ∀ v ∈ G

Wierzchołek może tworzyć krawędź ze wszystkimi innymi wierzchołkami z wyjątkiem samego siebie. Więc stopień wierzchołka będzie donumber of vertices in the graph minus 1. To 1 jest dla samo-wierzchołka, ponieważ nie może samodzielnie utworzyć pętli. Jeśli na którymkolwiek z wierzchołków znajduje się pętla, nie jest to prosty wykres.

Stopień wierzchołka można rozpatrywać w dwóch przypadkach grafów -

• Niekierowany wykres

• Kierowany wykres

Stopień wierzchołka na wykresie nieukierunkowanym

Graf nie skierowany nie ma skierowanych krawędzi. Rozważ następujące przykłady.

Example 1

Spójrz na poniższy wykres -

Na powyższym wykresie nieukierunkowanym

• deg (a) = 2, ponieważ w wierzchołku „a” spotykają się 2 krawędzie.

• deg (b) = 3, ponieważ w wierzchołku „b” spotykają się 3 krawędzie.

• deg (c) = 1, ponieważ w wierzchołku „c” jest 1 krawędź

• Więc „c” to a pendent vertex.

• deg (d) = 2, ponieważ w wierzchołku „d” spotykają się 2 krawędzie.

• deg (e) = 0, ponieważ jest 0 krawędzi utworzonych w wierzchołku „e”.

• Więc „e” to isolated vertex.

Example 2

Spójrz na poniższy wykres -

Na powyższym wykresie

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 i deg (e) = 0.

Wierzchołek „e” jest izolowanym wierzchołkiem. Wykres nie ma żadnego wiszącego wierzchołka.

Stopień wierzchołka na wykresie skierowanym

Na wykresie skierowanym każdy wierzchołek ma rozszerzenie indegree i outdegree.

Niezależność wykresu

• Nieokreślony wierzchołek V to liczba krawędzi, które wchodzą do wierzchołka V.

• Notation - deg− (V).

Stopień zaawansowania wykresu

• Poza wierzchołkiem V to liczba krawędzi wychodzących z wierzchołka V.

• Notation - st + (V).

Rozważ następujące przykłady.

Example 1

Spójrz na poniższy skierowany wykres. Wierzchołek „a” ma dwie krawędzie, „ad” i „ab”, które wychodzą na zewnątrz. W związku z tym jego stopniem zewnętrznym jest 2. Podobnie, istnieje krawędź „ga”, zbliżająca się do wierzchołka „a”. Stąd liczba nieokreślona „a” wynosi 1.

W poniższej tabeli przedstawiono stopnie i stopnie innych wierzchołków -

Wierzchołek	Indegree	Outdegree
za	1	2
b	2	0
do	2	1
re	1	1
mi	1	1
fa	1	1
sol	0	2

Example 2

Spójrz na poniższy skierowany wykres. Wierzchołek „a” ma krawędź „ae” wychodzącą na zewnątrz z wierzchołka „a”. Stąd jego stopień wyprzedza wynosi 1. Podobnie, wykres ma krawędź „ba” zbliżającą się do wierzchołka „a”. Stąd liczba nieokreślona „a” wynosi 1.

W poniższej tabeli przedstawiono stopnie i stopnie innych wierzchołków -

Wierzchołek	Indegree	Outdegree
za	1	1
b	0	2
do	2	0
re	1	1
mi	1	1

Wiszący wierzchołek

Używając stopnia wierzchołka, mamy dwa specjalne typy wierzchołków. Wierzchołek o stopniu pierwszym nazywa się wiszącym wierzchołkiem.

Example

Tutaj, w tym przykładzie, wierzchołek „a” i wierzchołek „b” mają połączoną krawędź „ab”. Tak więc w odniesieniu do wierzchołka „a” jest tylko jedna krawędź w kierunku wierzchołka „b” i podobnie w przypadku wierzchołka „b” jest tylko jedna krawędź w kierunku wierzchołka „a”. Wreszcie, wierzchołek „a” i wierzchołek „b” mają stopień, który jest również nazywany wierzchołkiem wiszącym.

Izolowany wierzchołek

Wierzchołek o stopniu zerowym nazywany jest wierzchołkiem izolowanym.

Example

Tutaj wierzchołek „a” i wierzchołek „b” nie mają żadnej łączności między sobą, a także z innymi wierzchołkami. Zatem stopień obu wierzchołków „a” i „b” wynosi zero. Są one również nazywane izolowanymi wierzchołkami.

Przyleganie

Oto normy sąsiedztwa -

• Na wykresie mówi się, że dwa wierzchołki są adjacent, jeśli między dwoma wierzchołkami jest krawędź. Tutaj przyleganie wierzchołków jest utrzymywane przez pojedynczą krawędź, która łączy te dwa wierzchołki.

• Na wykresie mówi się, że dwie krawędzie sąsiadują ze sobą, jeśli między nimi znajduje się wspólny wierzchołek. Tutaj przyleganie krawędzi jest utrzymywane przez pojedynczy wierzchołek, który łączy dwie krawędzie.

Example 1

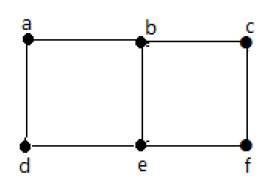
Na powyższym wykresie -

• „a” i „b” to sąsiednie wierzchołki, ponieważ między nimi istnieje wspólna krawędź „ab”.

• „a” i „d” to sąsiednie wierzchołki, ponieważ między nimi istnieje wspólna krawędź „ad”.

• ab ”i„ be ”to sąsiednie krawędzie, ponieważ między nimi znajduje się wspólny wierzchołek„ b ”.

• be ”i„ de ”to sąsiednie krawędzie, ponieważ między nimi znajduje się wspólny wierzchołek„ e ”.

Example 2

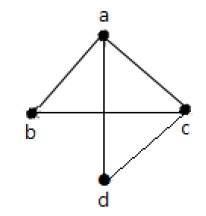
Na powyższym wykresie -

• „a” i „d” to sąsiednie wierzchołki, ponieważ między nimi istnieje wspólna krawędź „ad”.

• „c” i „b” to sąsiednie wierzchołki, ponieważ między nimi istnieje wspólna krawędź „cb”.

• „ad” i „cd” to sąsiednie krawędzie, ponieważ między nimi znajduje się wspólny wierzchołek „d”.

• „ac” i „cd” to sąsiednie krawędzie, ponieważ między nimi znajduje się wspólny wierzchołek „c”.

Równoległe krawędzie

Na wykresie, jeśli para wierzchołków jest połączona więcej niż jedną krawędzią, wtedy te krawędzie nazywane są krawędziami równoległymi.

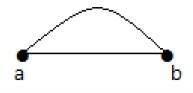
Na powyższym wykresie „a” i „b” to dwa wierzchołki połączone między nimi dwoma krawędziami „ab” i „ab”. Nazywa się to więc równoległą krawędzią.

Multi Graph

Wykres mający równoległe krawędzie jest znany jako Multigraph.

Example 1

Na powyższym wykresie jest pięć krawędzi „ab”, „ac”, „cd”, „cd” i „bd”. Ponieważ „c” i „d” mają między sobą dwie równoległe krawędzie, jest to Multigraph.

Example 2

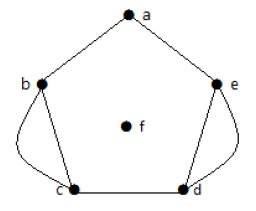
Na powyższym wykresie wierzchołki „b” i „c” mają dwie krawędzie. Wierzchołki „e” i „d” również mają między sobą dwie krawędzie. Dlatego jest to Multigraph.

Sekwencja stopni na wykresie

Jeśli stopnie wszystkich wierzchołków na wykresie są ułożone w porządku malejącym lub rosnącym, to uzyskana sekwencja nazywana jest sekwencją stopni na wykresie.

Example 1

Wierzchołek	ZA	b	do	re	mi
Łączenie z	pne	ogłoszenie	ogłoszenie	c, b, e	re
Stopień	2	2	2	3	1

Na powyższym wykresie, dla wierzchołków {d, a, b, c, e}, sekwencja stopni wynosi {3, 2, 2, 2, 1}.

Example 2

Wierzchołek	ZA	b	do	re	mi	fa
Łączenie z	być	a, c	b, d	c, e	ogłoszenie	-
Stopień	2	2	2	2	2	0

Na powyższym wykresie, dla wierzchołków {a, b, c, d, e, f}, sekwencja stopni wynosi {2, 2, 2, 2, 2, 0}.

Grafy mają różne właściwości, które służą do charakteryzowania grafów w zależności od ich struktury. Właściwości te są określone w specyficznych terminach związanych z dziedziną teorii grafów. W tym rozdziale omówimy kilka podstawowych właściwości, które są wspólne dla wszystkich wykresów.

Odległość między dwoma wierzchołkami

Jest to liczba krawędzi w najkrótszej ścieżce między wierzchołkiem U i wierzchołkiem V. Jeśli istnieje wiele ścieżek łączących dwa wierzchołki, najkrótsza ścieżka jest traktowana jako odległość między dwoma wierzchołkami.

Notacja - d (U, V)

Może istnieć dowolna liczba ścieżek od jednego wierzchołka do drugiego. Spośród nich musisz wybrać tylko najkrótszą.

Example

Spójrz na poniższy wykres -

Tutaj odległość od wierzchołka „d” do wierzchołka „e” lub po prostu „de” wynosi 1, ponieważ jest między nimi jedna krawędź. Istnieje wiele ścieżek od wierzchołka „d” do wierzchołka „e” -

• da, ab, be
• df, fg, ge
• de (Uwzględnia odległość między wierzchołkami)
• df, fc, ca, ab, be
• da, ac, cf, fg, ge

Ekscentryczność wierzchołka

Maksymalna odległość między wierzchołkiem a wszystkimi innymi wierzchołkami jest uważana za mimośrodowość wierzchołka.

Notacja - e (V)

Przyjmowana jest odległość od określonego wierzchołka do wszystkich innych wierzchołków na wykresie, a spośród tych odległości mimośrodowość jest największą z odległości.

Example

Na powyższym wykresie mimośrodowość „a” wynosi 3.

Odległość od „a” do „b” wynosi 1 („ab”),

od „a” do „c” to 1 („ac”),

od „a” do „d” wynosi 1 („ad”),

od „a” do „e” to 2 („ab” - „be”) lub („ad” - „de”),

od „a” do „f” to 2 („ac” - „cf”) lub („ad” - „df”),

od „a” do „g” wynosi 3 („ac” - „cf” - „fg”) lub („ad” - „df” - „fg”).

Zatem mimośrodowość wynosi 3, co stanowi maksimum względem wierzchołka „a” z odległości między „ag”, która jest maksimum.

Innymi słowy,

e (b) = 3

e (c) = 3

e (d) = 2

e (e) = 3

e (f) = 3

e (g) = 3

Promień połączonego wykresu

Minimalna mimośrodowość ze wszystkich wierzchołków jest uważana za promień wykresu G.Minimalna spośród wszystkich maksymalnych odległości między wierzchołkiem a wszystkimi innymi wierzchołkami jest uważana za promień wykresu G.

Notacja - r (G)

Ze wszystkich mimośrodów wierzchołków wykresu promień połączonego grafu jest minimum wszystkich tych mimośrodów.

Example

Na powyższym wykresie r (G) = 2, co jest minimalnym mimośrodem dla „d”.

Średnica wykresu

Maksymalna mimośrodowość ze wszystkich wierzchołków jest uważana za średnicę wykresu G.Maksymalne spośród wszystkich odległości między wierzchołkiem a wszystkimi innymi wierzchołkami jest uważane za średnicę wykresu G.

Notation − d(G) - Ze wszystkich mimośrodów wierzchołków wykresu, średnica połączonego grafu jest maksimum wszystkich tych mimośrodów.

Example

Na powyższym wykresie d (G) = 3; czyli maksymalna ekscentryczność.

Punkt centralny

Jeśli mimośrodowość wykresu jest równa jego promieniu, wówczas określa się go jako centralny punkt wykresu. Gdyby

e (V) = r (V),

wtedy „V” jest centralnym punktem wykresu „G”.

Example

Na przykładowym wykresie „d” jest centralnym punktem wykresu.

e (d) = r (d) = 2

Środek

Zbiór wszystkich centralnych punktów „G” nazywany jest środkiem wykresu.

Example

Na przykładowym wykresie {'d'} jest środkiem wykresu.

Obwód

Plik number of edges in the longest cycle of ‘G’ nazywany jest obwodem „G”.

Example

Na przykładowym wykresie obwód wynosi 6, który wyprowadziliśmy z najdłuższego cyklu acfgeba lub acfdeba.

Obwód

Liczba krawędzi w najkrótszym cyklu „G” nazywana jest jego Obwodem.

Notation: g (G).

Example - Na przykładowym wykresie obwód wykresu wynosi 4, który wyprowadziliśmy z najkrótszego cyklu acfda lub dfged lub abeda.

Twierdzenie o sumie stopni wierzchołków

Jeśli G = (V, E) jest grafem niekierowanym z wierzchołkami V = {V ₁ , V ₂ ,… V _n } to

n Σ i = 1 stopień (V _i ) = 2 | E |

Corollary 1

Jeśli G = (V, E) jest grafem skierowanym z wierzchołkami V = {V ₁ , V ₂ ,… V _n }, to

n Σ i = 1 stopień + (V _i ) = | E | = n Σ i = 1 deg− (V _i )

Corollary 2

Na każdym grafie niekierowanym liczba wierzchołków z nieparzystym stopniem jest parzysta.

Corollary 3

W grafie niekierowanym, jeśli stopień każdego wierzchołka wynosi k, to

k | V | = 2 | E |

Corollary 4

W grafie niekierowanym, jeśli stopień każdego wierzchołka wynosi co najmniej k, to

k | V | ≤ 2 | E |

| Corollary 5

W grafie niekierowanym, jeśli stopień każdego wierzchołka wynosi co najwyżej k, to

k | V | ≥ 2 | E |

Istnieją różne typy grafów w zależności od liczby wierzchołków, liczby krawędzi, wzajemnych połączeń i ich ogólnej struktury. W tym rozdziale omówimy tylko kilka ważnych typów wykresów.

Wykres zerowy

A graph having no edges nazywa się wykresem zerowym.

Przykład

Na powyższym wykresie znajdują się trzy wierzchołki nazwane „a”, „b” i „c”, ale nie ma między nimi żadnych krawędzi. Stąd jest to wykres zerowy.

Wykres trywialny

ZA graph with only one vertex nazywa się wykresem trywialnym.

Przykład

Na powyższym wykresie jest tylko jeden wierzchołek „a” bez innych krawędzi. Stąd jest to wykres trywialny.

Wykres niekierowany

Wykres niekierowany zawiera krawędzie, ale krawędzie nie są skierowane.

Przykład

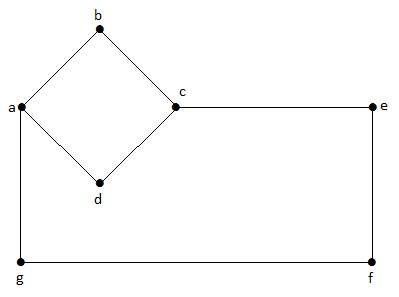
Na tym wykresie „a”, „b”, „c”, „d”, „e”, „f”, „g” to wierzchołki, a „ab”, „bc”, „cd”, „da „,„ ag ”,„ gf ”,„ ef ”to krawędzie wykresu. Ponieważ jest to wykres niekierowany, krawędzie „ab” i „ba” są takie same. Podobnie inne krawędzie również rozpatrywane w ten sam sposób.

Kierowany wykres

Na wykresie skierowanym każda krawędź ma kierunek.

Przykład

Na powyższym wykresie mamy siedem wierzchołków „a”, „b”, „c”, „d”, „e”, „f” i „g” oraz osiem krawędzi „ab”, „cb”, „ dc ”,„ ad ”,„ ec ”,„ fe ”,„ gf ”i„ ga ”. Ponieważ jest to wykres skierowany, na każdej krawędzi znajduje się strzałka wskazująca kierunek. Zauważ, że na wykresie skierowanym „ab” różni się od „ba”.

Prosty wykres

Wykres with no loops i nie parallel edges nazywa się prostym wykresem.

• Maksymalna liczba krawędzi możliwych na pojedynczym grafie z „n” wierzchołkami to ⁿ C _2, gdzie ⁿ C ₂ = n (n - 1) / 2.

• Liczba prostych grafów możliwych przy 'n' wierzchołkach = 2 _{ⁿ c 2} = 2 ^{n (n-1) / 2} .

Przykład

Na poniższym wykresie są 3 wierzchołki z 3 krawędziami, które są maksymalnie wykluczone z równoległych krawędzi i pętli. Można to udowodnić za pomocą powyższych wzorów.

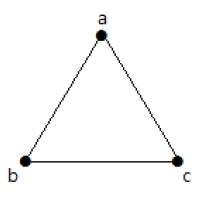
Maksymalna liczba krawędzi z n = 3 wierzchołkami -

ⁿ C ₂ = n (n – 1) / 2

= 3 (3–1) / 2

= 6/2

= 3 krawędzie

Maksymalna liczba prostych grafów z n = 3 wierzchołkami -

2 _{ⁿ C 2} = 2 ^{n (n-1) / 2}

= 2 ^{3 (3-1) / 2}

= 2 ³

8

Te 8 wykresów jest pokazanych poniżej -

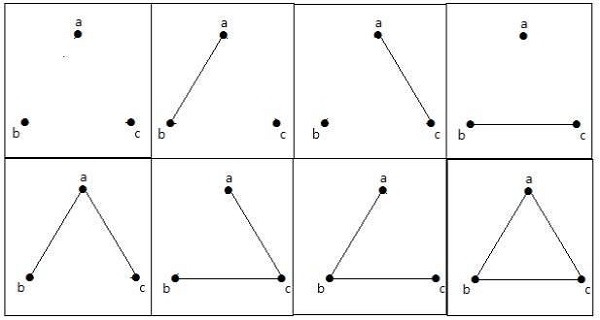
Połączony wykres

Mówi się, że wykres G jest połączony if there exists a path between every pair of vertices. Każdy wierzchołek wykresu powinien mieć co najmniej jedną krawędź. Abyśmy mogli powiedzieć, że jest połączony z innym wierzchołkiem po drugiej stronie krawędzi.

Przykład

Na poniższym wykresie każdy wierzchołek ma własną krawędź połączoną z inną krawędzią. Stąd jest to połączony wykres.

Disconnected Graph

Graf G jest odłączany, jeśli nie zawiera co najmniej dwóch połączonych wierzchołków.

Przykład 1

Poniższy wykres jest przykładem odłączonego wykresu, w którym istnieją dwa składniki, jeden z wierzchołkami „a”, „b”, „c”, „d”, a drugi z „e”, „f”, „g”, wierzchołki „h”.

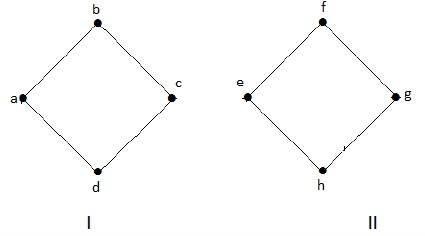
Te dwa elementy są niezależne i nie są ze sobą połączone. Dlatego nazywa się to wykresem odłączonym.

Przykład 2

W tym przykładzie istnieją dwa niezależne komponenty, abfe i cd, które nie są ze sobą połączone. Stąd jest to odłączony wykres.

Regularny wykres

Mówi się, że wykres G jest regularny, if all its vertices have the same degree. Na grafie, jeśli stopień każdego wierzchołka wynosi „k”, wówczas wykres nazywany jest „grafem k-regularnym”.

Przykład

Na poniższych wykresach wszystkie wierzchołki mają ten sam stopień. Więc te wykresy nazywane są zwykłymi wykresami.

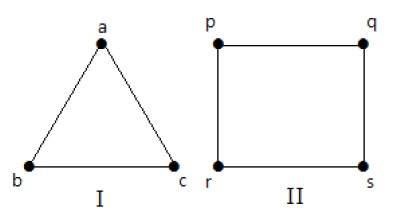
Na obu wykresach wszystkie wierzchołki mają stopień 2. Nazywa się to 2-regularnymi grafami.

Kompletny wykres

Prosty graf z „n” wzajemnymi wierzchołkami nazywa się grafem całkowitym i tak właśnie jest denoted by ‘K_n’. Na wykresiea vertex should have edges with all other vertices, to nazwał pełny wykres.

Innymi słowy, jeśli wierzchołek jest połączony ze wszystkimi innymi wierzchołkami na grafie, nazywa się go pełnym grafem.

Przykład

Na poniższych wykresach każdy wierzchołek grafu jest połączony ze wszystkimi pozostałymi wierzchołkami wykresu, z wyjątkiem samego siebie.

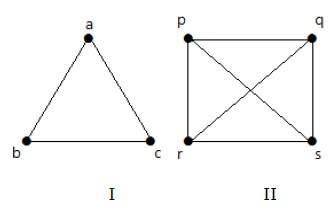
Na wykresie I

	za	b	do
za	Nie połączony	Połączony	Połączony
b	Połączony	Nie połączony	Połączony
do	Połączony	Połączony	Nie połączony

Na wykresie II

	p	q	r	s
p	Nie połączony	Połączony	Połączony	Połączony
q	Połączony	Nie połączony	Połączony	Połączony
r	Połączony	Połączony	Nie połączony	Połączony
s	Połączony	Połączony	Połączony	Nie połączony

Wykres cyklu

Prosty wykres z wierzchołkami „n” (n> = 3) i krawędziami „n” nazywany jest grafem cyklicznym, jeśli wszystkie jego krawędzie tworzą cykl o długości „n”.

Jeśli stopień każdego wierzchołka na wykresie wynosi dwa, nazywa się to wykresem cyklicznym.

Notation- C _n

Przykład

Spójrz na poniższe wykresy -

• Wykres I ma 3 wierzchołki z 3 krawędziami, które tworzą cykl „ab-bc-ca”.

• Graf II ma 4 wierzchołki z 4 krawędziami, które tworzą cykl „pq-qs-sr-rp”.

• Wykres III ma 5 wierzchołków z 5 krawędziami, które tworzą cykl „ik-km-ml-lj-ji”.

Stąd wszystkie podane wykresy są wykresami cykli.

Wykres koła

Wykres kołowy uzyskuje się z wykresu cyklu C _n-1 przez dodanie nowego wierzchołka. Ten nowy wierzchołek nazywa się aHubktóry jest połączony ze wszystkimi wierzchołkami C _n .

Notacja - W _n

Liczba krawędzi w W _n = Liczba krawędzi od piasty do wszystkich innych wierzchołków +

Liczba krawędzi ze wszystkich innych węzłów na wykresie cyklu bez piasty.

= (n – 1) + (n – 1)

= 2 (n – 1)

Przykład

Spójrz na poniższe wykresy. Wszystkie są wykresami kołowymi.

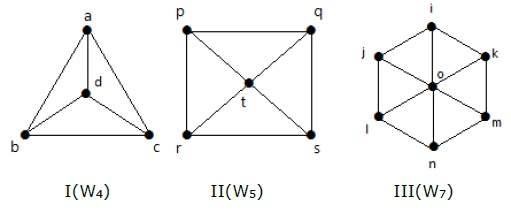
Na wykresie I otrzymujemy go z C ₃ przez dodanie wierzchołka w środku nazwanego „d”. Jest oznaczony jako W ₄ .

Liczba krawędzi w W4 = 2 (n-1) = 2 (3) = 6

Na wykresie II otrzymujemy go z C4 przez dodanie wierzchołka w środku nazwanego „t”. Jest oznaczony jako W ₅ .

Liczba krawędzi w W5 = 2 (n-1) = 2 (4) = 8

Na wykresie III otrzymujemy go z C ₆ przez dodanie wierzchołka w środku o nazwie „o”. Jest oznaczony jako W ₇ .

Liczba krawędzi w W4 = 2 (n-1) = 2 (6) = 12

Wykres cykliczny

Wykres with at least one cykl nazywany jest wykresem cyklicznym.

Przykład

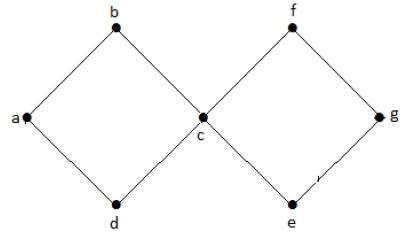
Na powyższym przykładowym wykresie mamy dwa cykle abcda i cfgec. Dlatego nazywa się to wykresem cyklicznym.

Graf acykliczny

Wykres with no cycles nazywany jest grafem acyklicznym.

Przykład

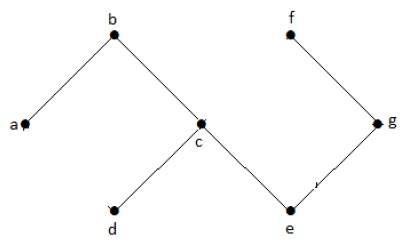
Na powyższym przykładowym wykresie nie mamy żadnych cykli. Stąd jest to wykres niecykliczny.

Wykres dwudzielny

Prosty graf G = (V, E) z podziałem wierzchołków V = {V ₁ , V ₂ } nazywany jest grafem dwudzielnymif every edge of E joins a vertex in V1 to a vertex in V₂.

Generalnie graf bipertytowy ma dwa zbiory wierzchołków, powiedzmy V1 i V2, i jeśli rysuje się krawędź, powinien łączyć dowolny wierzchołek ze zbioru V ₁ z dowolnym wierzchołkiem w zbiorze V ₂ .

Przykład

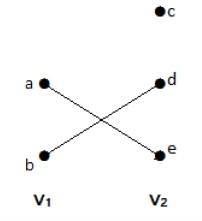
Na tym wykresie można zaobserwować dwa zestawy wierzchołków - V ₁ i V ₂ . Tutaj dwie krawędzie nazwane „ae” i „bd” łączą wierzchołki dwóch zbiorów V ₁ i V ₂ .

Kompletny wykres dwudzielny

Graf dwudzielny „G”, G = (V, E) z podziałem V = {V ₁ , V ₂ } mówi się, że jest pełnym grafem dwudzielnym, jeśli każdy wierzchołek w V ₁ jest połączony z każdym wierzchołkiem V ₂ .

Ogólnie rzecz biorąc, pełny dwudzielny graf łączy każdy wierzchołek ze zbioru V ₁ z każdym wierzchołkiem ze zbioru V ₂ .

Przykład

Poniższy wykres jest pełnym grafem dwudzielnym, ponieważ ma krawędzie łączące każdy wierzchołek ze zbioru V ₁ z każdym wierzchołkiem ze zbioru V ₂ .

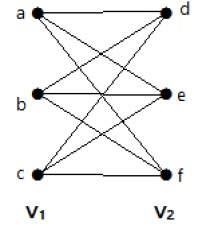
Jeśli | V ₁ | = mi | V ₂ | = n, to pełny wykres dwudzielny oznaczamy przez K _{m, n} .

• K _{m, n} ma (m + n) wierzchołki i (mn) krawędzie.
• K _{m, n} jest wykresem regularnym, jeśli m = n.

Ogólnie rzecz biorąc, a complete bipartite graph is not a complete graph.

K _{m, n} jest pełnym wykresem, jeśli m = n = 1.

Maksymalna liczba krawędzi w grafie dwudzielnym z n wierzchołkami wynosi -

[N ² /4]

Jeżeli n = 10, K5, 5 = [N2 / 4] = [10 ² /4] = 25.

Podobnie K6, 4 = 24

K7, 3 = 21

K8, 2 = 16

K9, 1 = 9

Jeśli n = 9, k5, 4 = [n2 / 4] = [92/4] = 20

Podobnie K6, 3 = 18

K7, 2 = 14

K8, 1 = 8

„G” jest dwudzielnym wykresem, jeśli „G” nie ma cykli o nieparzystej długości. Szczególnym przypadkiem grafu dwudzielnego jest graf gwiaździsty.

Wykres gwiazdowy

Kompletny graf dwudzielny postaci K1, n-1 jest grafem gwiazdowym z n-wierzchołkami. Graf gwiazdowy jest pełnym grafem dwudzielnym, jeśli pojedynczy wierzchołek należy do jednego zbioru, a wszystkie pozostałe wierzchołki należą do drugiego.

Przykład

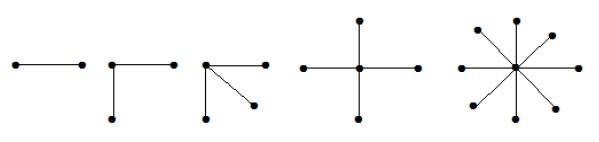
Na powyższych wykresach, z „n” wierzchołków, wszystkie „n – 1” wierzchołków są połączone z pojedynczym wierzchołkiem. Stąd ma postać K ¹ , ^n-1, które są gwiazdografami.

Uzupełnienie wykresu

Niech 'G−' będzie prostym grafem z niektórymi wierzchołkami takimi jak 'G', a krawędź {U, V} jest obecna w 'G−', jeśli krawędź nie jest obecna w G. Oznacza to, że dwa wierzchołki sąsiadują ze sobą w 'G−', jeśli dwa wierzchołki nie sąsiadują ze sobą w G.

Jeśli krawędzie, które istnieją na wykresie I, są nieobecne na innym wykresie II, i jeśli zarówno wykres I, jak i wykres II są połączone razem, tworząc pełny wykres, wówczas wykres I i wykres II nazywane są wzajemnymi uzupełnieniami.

Przykład

W poniższym przykładzie wykres-I ma dwie krawędzie „cd” i „bd”. Jego dopełnienie graf-II ma cztery krawędzie.

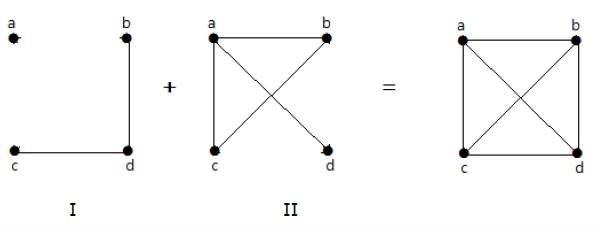
Zauważ, że krawędzie na wykresie-I nie występują na wykresie-II i odwrotnie. Stąd połączenie obu wykresów daje pełny wykres „n” wierzchołków.

Note - Połączenie dwóch uzupełniających się wykresów daje pełny wykres.

Jeśli „G” jest prostym wykresem, to

| E (G) | + | E („G -”) | = | E (Kn) |, gdzie n = liczba wierzchołków na wykresie.

Przykład

Niech „G” będzie prostym grafem z dziewięcioma wierzchołkami i dwunastoma krawędziami, znajdź liczbę krawędzi w „G-”.

Masz, | E (G) | + | E („G -”) | = | E (Kn) |

12 + | E („G -”) | =

9 (9-1) / 2 = ⁹ C ₂

12 + | E („G -”) | = 36

| E („G -”) | = 24

„G” jest prostym wykresem z 40 krawędziami, a jego dopełnienie „G−” ma 38 krawędzi. Znajdź liczbę wierzchołków w grafie G lub „G−”.

Niech liczba wierzchołków na grafie będzie równa „n”.

Mamy, | E (G) | + | E („G -”) | = | E (Kn) |

40 + 38 = n (n-1) / 2

156 = n (n-1)

13 (12) = n (n-1)

n = 13

Drzewa to wykresy, które nie zawierają ani jednego cyklu. Reprezentują hierarchiczną strukturę w formie graficznej. Drzewa należą do najprostszych klas grafów. Pomimo swojej prostoty mają bogatą strukturę.

Drzewa zapewniają szereg użytecznych aplikacji, od prostych, jak drzewo genealogiczne, po tak złożone, jak drzewa w strukturach danych informatycznych.

Drzewo

ZA connected acyclic graphnazywa się drzewem. Innymi słowy, połączony wykres bez cykli nazywany jest drzewem.

Krawędzie drzewa są znane jako branches. Elementy drzew nazywane są ich węzłami. Nazywane są węzły bez węzłów potomnychleaf nodes.

Drzewo z „n” wierzchołkami ma „n-1” krawędzi. Jeśli ma jeszcze jedną krawędź więcej niż „n-1”, to ta dodatkowa krawędź powinna oczywiście łączyć się z dwoma wierzchołkami, co prowadzi do utworzenia cyklu. Następnie staje się wykresem cyklicznym, co jest naruszeniem dla wykresu drzewiastego.

Example 1

Wykres pokazany tutaj jest drzewem, ponieważ nie ma cykli i jest połączony. Ma cztery wierzchołki i trzy krawędzie, tj. Dla „n” wierzchołków „n-1” krawędzi, jak wspomniano w definicji.

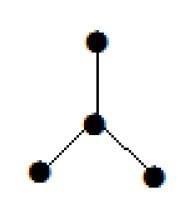
Note - Każde drzewo ma co najmniej dwa wierzchołki pierwszego stopnia.

Example 2

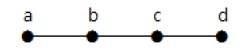
W powyższym przykładzie wierzchołki „a” i „d” mają stopień pierwszy. A pozostałe dwa wierzchołki „b” i „c” mają stopień drugi. Jest to możliwe, ponieważ aby nie tworzyć cyklu, w dowolnym miejscu wykresu powinny znajdować się co najmniej dwie pojedyncze krawędzie. To nic innego jak dwie krawędzie z jednym stopniem.

Las

ZA disconnected acyclic graphnazywa się lasem. Innymi słowy, rozłączny zbiór drzew nazywany jest lasem.

Example

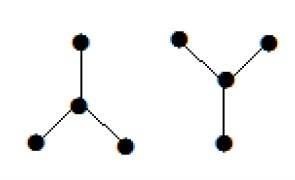
Poniższy wykres wygląda jak dwa pod-wykresy; ale jest to pojedynczy odłączony wykres. Na tym wykresie nie ma cykli. Stąd ewidentnie jest to las.

Drzewa spinające

Niech G będzie grafem połączonym, wtedy pod-graf H z G nazywany jest drzewem rozpinającym G, jeśli -

• H to drzewo
• H zawiera wszystkie wierzchołki G.

Drzewo rozpinające T grafu niekierowanego G to podgraf zawierający wszystkie wierzchołki G.

Example

W powyższym przykładzie G jest połączonym wykresem, a H jest pod-wykresem G.

Oczywiście wykres H nie ma cykli, jest to drzewo o sześciu krawędziach, czyli o jeden mniej niż całkowita liczba wierzchołków. Stąd H jest drzewem opinającym G.

Ranking obwodu

Niech „G” będzie grafem połączonym z „n” wierzchołkami i „m” krawędziami. Drzewo opinające „T” G zawiera (n-1) krawędzi.

Dlatego liczba krawędzi, które należy usunąć z `` G '', aby uzyskać drzewo opinające = m- (n-1), które nazywa się rangą obwodu G.

Ta formuła jest prawdziwa, ponieważ w drzewie rozpinającym musisz mieć krawędzi „n-1”. Poza krawędziami „m” musisz zachować na wykresie krawędzi „n – 1”.

Stąd usunięcie krawędzi „n – 1” z „m” daje krawędzie, które należy usunąć z wykresu w celu uzyskania drzewa opinającego, które nie powinno tworzyć cyklu.

Example

Spójrz na poniższy wykres -

Dla wykresu podanego w powyższym przykładzie masz m = 7 krawędzi in = 5 wierzchołków.

Wtedy ranga obwodu to -

G = m - (n - 1)

= 7 - (5 - 1)

= 3

Example

Niech „G” będzie grafem połączonym z sześcioma wierzchołkami, a stopień każdego z nich wynosi trzy. Znajdź rangę obwodu „G”.

Twierdzenie o sumie stopni wierzchołków

n Σ i=1deg (V _i ) = 2 | E |

6 × 3 = 2 | E |

| E | = 9

Ranking obwodu = | E | - (| V | - 1)

= 9 - (6 - 1) = 4

Twierdzenie Kirchoffa

Twierdzenie Kirchoffa jest przydatne w znajdowaniu liczby drzew rozpinających, które można utworzyć z połączonego wykresu.

Example

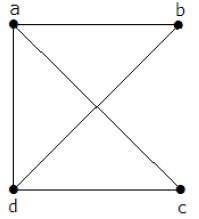
Macierz „A” powinna być wypełniona tak, jakby między dwoma wierzchołkami istniała krawędź, to należy ją podać jako „1”, w przeciwnym razie „0”.

$$A=\begin{vmatrix}0 & a & b & c & d\\a & 0 & 1 & 1 & 1 \\b & 1 & 0 & 0 & 1\\c & 1 & 0 & 0 & 1\\d & 1 & 1 & 1 & 0 \end{vmatrix} = \begin{vmatrix} 0 & 1 & 1 & 1\\1 & 0 & 0 & 1\\1 & 0 & 0 & 1\\1 & 1 & 1 & 0\end{vmatrix}$$

Korzystając z twierdzenia Kirchoffa, należy je zmienić, zastępując podstawowe wartości przekątnych stopniem wierzchołków, a wszystkie inne elementy - -1.

$$=\begin{vmatrix} 3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix}=M$$ $$M=\begin{vmatrix}3 & -1 & -1 & -1\\-1 & 2 & 0 & -1\\-1 & 0 & 2 & -1\\-1 & -1 & -1 & 3 \end{vmatrix} =8$$ $$Co\:\:factor\:\:of\:\:m1\:\:= \begin{vmatrix} 2 & 0 & -1\\0 & 2 & -1\\-1 & -1 & 3\end{vmatrix}$$

Zatem liczba drzew rozpinających = 8.

To, czy możliwe jest przejście grafu z jednego wierzchołka do drugiego, zależy od tego, w jaki sposób graf jest połączony. Łączność to podstawowa koncepcja w teorii grafów. Łączność określa, czy wykres jest połączony, czy odłączony. Zawiera podtematy oparte na krawędzi i wierzchołku, znane jako łączność krawędzi i łączność wierzchołków. Omówmy je szczegółowo.

Łączność

Mówi się, że jest to wykres connected if there is a path between every pair of vertex. Od każdego wierzchołka do każdego innego wierzchołka powinna być jakaś ścieżka do przejścia. Nazywa się to łącznością wykresu. Mówi się, że graf z wieloma rozłączonymi wierzchołkami i krawędziami jest rozłączony.

Example 1

Na poniższym wykresie można przejść od jednego wierzchołka do dowolnego innego wierzchołka. Na przykład, można przejść od wierzchołka „a” do wierzchołka „e”, używając ścieżki „ab-e”.

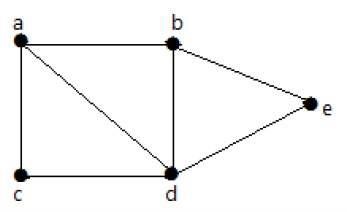
Example 2

W poniższym przykładzie przejście od wierzchołka „a” do wierzchołka „f” nie jest możliwe, ponieważ nie ma między nimi bezpośredniej lub pośredniej ścieżki. Stąd jest to odłączony wykres.

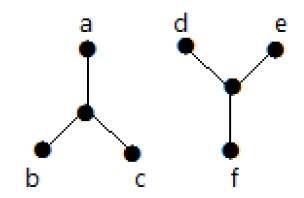
Wytnij wierzchołek

Niech „G” będzie grafem połączonym. Wierzchołek V ∈ G nazywany jest wierzchołkiem ciętym „G”, jeśli „G-V” (Usuń „V” z „G”) daje w wyniku rozłączony wykres. Usunięcie wyciętego wierzchołka z wykresu dzieli go na dwa lub więcej wykresów.

Note - Usunięcie przecięcia wierzchołka może spowodować odłączenie wykresu.

Połączony graf „G” może mieć najwyżej (n – 2) przecięte wierzchołki.

Example

Na poniższym wykresie wierzchołki „e” i „c” to przecięte wierzchołki.

Po usunięciu „e” lub „c” wykres stanie się wykresem odłączonym.

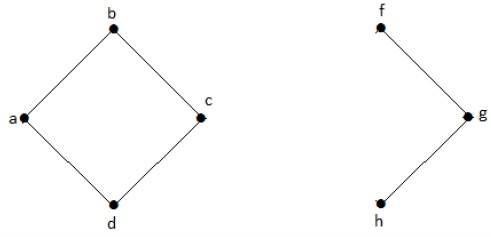
Bez „g” nie ma ścieżki między wierzchołkiem „c” a wierzchołkiem „h” i wieloma innymi. Stąd jest to odłączony graf z przeciętym wierzchołkiem jako „e”. Podobnie „c” jest również wyciętym wierzchołkiem dla powyższego wykresu.

Cut Edge (Bridge)

Niech „G” będzie grafem połączonym. Krawędź „e” ∈ G nazywana jest krawędzią tnącą, jeśli „G-e” daje w wyniku odłączony wykres.

Jeśli usunięcie krawędzi wykresu skutkuje powstaniem dwóch lub więcej wykresów, wówczas ta krawędź nazywana jest krawędzią tnącą.

Example

Na poniższym wykresie krawędź cięcia to [(c, e)].

Po usunięciu krawędzi (c, e) z wykresu staje się on odłączonym wykresem.

Na powyższym wykresie usunięcie krawędzi (c, e) dzieli wykres na dwie części, które są niczym innym jak odłączonym wykresem. Stąd krawędź (c, e) jest ciętą krawędzią wykresu.

Note - Niech więc „G” będzie grafem połączonym z „n” wierzchołkami

• krawędź cięcia e ∈ G wtedy i tylko wtedy, gdy krawędź „e” nie jest częścią żadnego cyklu w G.

• maksymalna możliwa liczba krawędzi ciętych wynosi „n-1”.

• zawsze, gdy istnieją krawędzie cięte, istnieją również wierzchołki cięte, ponieważ co najmniej jeden wierzchołek krawędzi cięcia jest wierzchołkiem ciętym.

• jeśli przecięty wierzchołek istnieje, wówczas krawędź cięcia może istnieć lub nie.

Wytnij zestaw wykresu

Niech „G” = (V, E) będzie grafem połączonym. Podzbiór E 'z E jest nazywany zbiorem ciętym G, jeśli usunięcie wszystkich krawędzi E' z G powoduje odłączenie G.

Jeśli usunięcie pewnej liczby krawędzi z wykresu powoduje jego rozłączenie, wówczas te usunięte krawędzie nazywane są zbiorem cięć wykresu.

Example

Spójrz na poniższy wykres. Jego zestaw cięć to E1 = {e1, e3, e5, e8}.

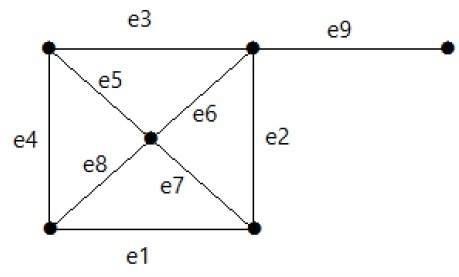
Po usunięciu zbioru cięć E1 z wykresu wyglądałoby to następująco -

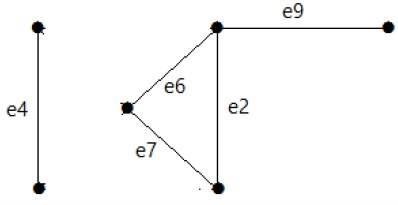
Podobnie istnieją inne zestawy cięć, które mogą odłączyć wykres -

• E3 = {e9} - Najmniejszy wycięty zbiór wykresu.

• E4 = {e3, e4, e5}

Edge Connectivity

Niech „G” będzie grafem połączonym. Minimalna liczba krawędzi, których usunięcie powoduje rozłączenie „G”, nazywana jest łącznością krawędzi G.

Notation - λ (G)

Innymi słowy, plik number of edges in a smallest cut set of G nazywana jest łącznością brzegową G.

Jeśli „G” ma wyciętą krawędź, to λ (G) wynosi 1. (łączność krawędzi G.)

Example

Spójrz na poniższy wykres. Po usunięciu dwóch minimalnych krawędzi połączony wykres zostaje rozłączony. Stąd jego łączność krawędziowa (λ (G)) wynosi 2.

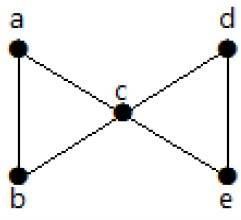
Oto cztery sposoby odłączenia wykresu przez usunięcie dwóch krawędzi -

Łączność z wierzchołkami

Niech „G” będzie grafem połączonym. Minimalna liczba wierzchołków, których usunięcie powoduje rozłączenie „G” lub zmniejszenie „G” do trywialnego grafu, nazywa się jego łącznością wierzchołków.

Notation - K (G)

Example

Na powyższym wykresie usunięcie wierzchołków „e” i „i” powoduje odłączenie wykresu.

Jeśli G ma przecięty wierzchołek, to K (G) = 1.

Notation - dla dowolnego połączonego wykresu G,

K (G) ≤ λ (G) ≤ δ (G)

Łączność wierzchołków (K (G)), łączność krawędzi (λ (G)), minimalna liczba stopni G (δ (G)).

Example

Obliczyć λ (G) i K (G) dla następującego wykresu -

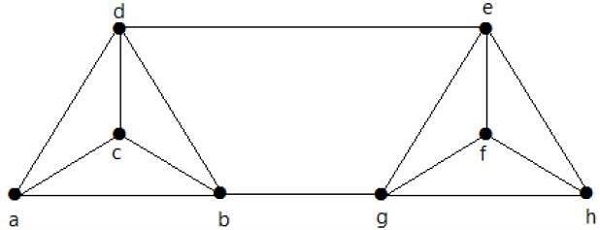
Solution

Z wykresu

δ (G) = 3

K (G) ≤ λ (G) ≤ δ (G) = 3 (1)

K (G) ≥ 2 (2)

Usuwając krawędzie {d, e} i {b, h}, możemy odłączyć G.

W związku z tym,

λ (G) = 2

2 ≤ λ (G) ≤ δ (G) = 2 (3)

Z (2) i (3), łączność wierzchołków K (G) = 2

Graf pokrywający to podgraf, który zawiera albo wszystkie wierzchołki, albo wszystkie krawędzie odpowiadające innemu grafowi. Podgraf zawierający wszystkie wierzchołki nazywa się aline/edge covering. Podgraf, który zawiera wszystkie krawędzie, nazywa się avertex covering.

Pokrycie linii

Niech G = (V, E) będzie wykresem. Podzbiór C (E) nazywany jest pokryciem linii G, jeśli każdy wierzchołek G przypada na co najmniej jedną krawędź w C, tj.

deg (V) ≥ 1 ∀ V ∈ G

ponieważ każdy wierzchołek jest połączony z innym wierzchołkiem krawędzią. W związku z tym ma minimalny stopień 1.

Example

Spójrz na poniższy wykres -

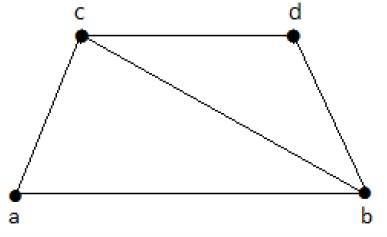
Jego podgrafy mające pokrycie linii są następujące:

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Pokrycie linii „G” nie istnieje wtedy i tylko wtedy, gdy „G” ma izolowany wierzchołek. Pokrycie linii wykresu z „n” wierzchołkami ma co najmniej [n / 2] krawędzi.

Minimalne pokrycie linii

Mówi się, że linia pokrywająca C wykresu G jest minimalna if no edge can be deleted from C.

Example

Na powyższym wykresie podgrafy z pokryciem linii są następujące -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Tutaj C ₁ , C ₂ , C ₃ to minimalne pokrycia linii, podczas gdy C ₄ nie, ponieważ możemy usunąć {b, c}.

Minimalne pokrycie linii

Jest również znany jako Smallest Minimal Line Covering. Minimalne pokrycie linii z minimalną liczbą krawędzi nazywa się minimalnym pokryciem linii „G”. Liczba krawędzi w minimalnym pokryciu linii w „G” nazywana jestline covering number„G” (α ₁ ).

Example

W powyższym przykładzie C ₁ i C ₂ to minimalne pokrycie linii G i α ₁ = 2.

• Każde pokrycie linii zawiera minimalne pokrycie linii.

• Każde pokrycie linii nie zawiera minimalnego pokrycia linii (C ₃ nie zawiera żadnego minimalnego pokrycia linii.

• Brak minimalnego pokrycia linii zawiera cykl.

• Jeśli linia obejmująca „C” nie zawiera ścieżek o długości 3 lub więcej, to „C” jest minimalnym pokryciem linii, ponieważ wszystkie składowe „C” są gwiazdami, a z gwiezdnego grafu nie można usunąć żadnej krawędzi.

Pokrycie wierzchołków

Niech „G” = (V, E) będzie wykresem. Podzbiór K z V nazywany jest pokryciem wierzchołka „G”, jeśli każda krawędź „G” styka się z wierzchołkiem w „K” lub jest przez nie pokryta.

Example

Spójrz na poniższy wykres -

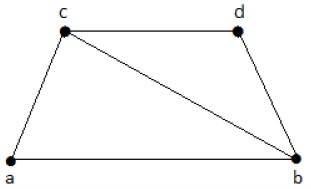
Podgrafy, które można wyprowadzić z powyższego wykresu, są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

Tutaj K ₁ , K ₂ i K ₃ mają pokrycie wierzchołków, podczas gdy K ₄ nie ma żadnego pokrycia wierzchołków, ponieważ nie zakrywa krawędzi {bc}.

Minimalne pokrycie wierzchołków

Mówi się, że wierzchołek „K” wykresu „G” stanowi minimalne pokrycie wierzchołków, jeśli żaden wierzchołek nie może zostać usunięty z „K”.

Example

Na powyższym wykresie podgrafy mające pokrycie wierzchołków są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Tutaj K ₁ i K ₂ są minimalnymi pokryciami wierzchołków, podczas gdy w K ₃ wierzchołek „d” można usunąć.

Minimalne pokrycie wierzchołków

Jest również znany jako najmniejsze minimalne pokrycie wierzchołków. Minimalne pokrycie wierzchołków grafu „G” minimalną liczbą wierzchołków nazywa się minimalnym pokryciem wierzchołków.

Liczba wierzchołków w minimalnym pokryciu wierzchołków „G” jest nazywana liczbą obejmującą wierzchołki G (α ₂ ).

Example

Na poniższym wykresie podgrafy mające pokrycie wierzchołków są następujące -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Tutaj K ₁ jest minimalnym pokryciem wierzchołka G, ponieważ ma tylko dwa wierzchołki. α ₂ = 2.

Dopasowany wykres to podgraf wykresu, w którym nie ma krawędzi sąsiadujących ze sobą. Po prostu nie powinno być żadnego wspólnego wierzchołka między dowolnymi dwoma krawędziami.

Pasujący

Niech „G” = (V, E) będzie wykresem. Podgraf nazywa się pasującym M (G),if each vertex of G is incident with at most one edge in Mtj.

deg (V) ≤ 1 ∀ V ∈ G

co oznacza, że ​​w dopasowanym grafie M (G) wierzchołki powinny mieć stopień 1 lub 0, gdzie krawędzie powinny padać z wykresu G.

Notation - M (G)

Example

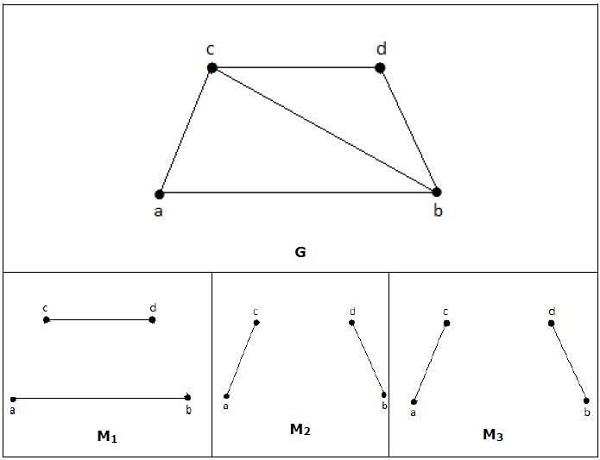
W dopasowaniu

jeśli deg (V) = 1, to mówi się, że (V) jest dopasowane

jeśli deg (V) = 0, to (V) nie jest dopasowywane.

W dopasowaniu żadne dwie krawędzie nie sąsiadują ze sobą. Dzieje się tak, ponieważ jeśli jakiekolwiek dwie krawędzie sąsiadują ze sobą, wówczas stopień wierzchołka, który łączy te dwie krawędzie, będzie miał stopień 2, co narusza regułę dopasowania.

Maksymalne dopasowanie

Mówi się, że dopasowanie M wykresu „G” jest maksymalne if no other edges of ‘G’ can be added to M.

Example

M1, M2, M3 z powyższego wykresu to maksymalne dopasowanie G.

Maksymalne dopasowanie

Jest również znany jako największe maksymalne dopasowanie. Maksymalne dopasowanie definiuje się jako maksymalne dopasowanie z maksymalną liczbą krawędzi.

Liczba krawędzi w maksymalnym dopasowaniu „G” jest nazywana jego matching number.

Example

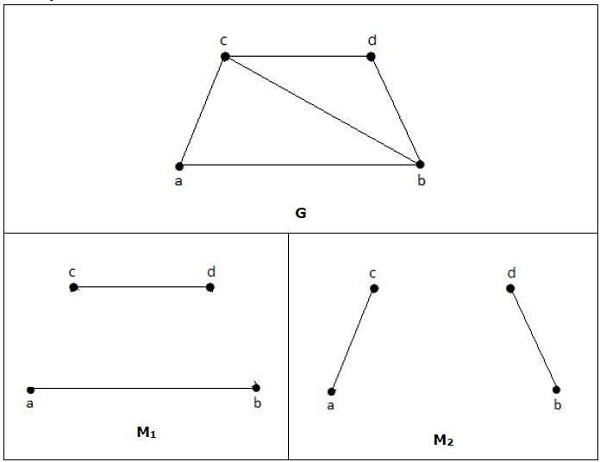
Dla wykresu podanego w powyższym przykładzie M1 i M2 są maksymalnym dopasowaniem „G”, a jego pasująca liczba to 2. Stąd korzystając z wykresu G, możemy utworzyć tylko podgrafy z maksymalnie 2 krawędziami. Dlatego mamy pasującą liczbę jako dwa.

Idealne dopasowanie

Mówi się, że dopasowanie (M) wykresu (G) jest idealnym dopasowaniem, jeśli każdy wierzchołek wykresu g (G) przypada dokładnie na jedną krawędź dopasowania (M), tj.

deg (V) = 1 ∀ V

Stopień każdego wierzchołka w podgrafie powinien mieć stopień 1.

Example

Na poniższych wykresach M1 i M2 są przykładami doskonałego dopasowania G.

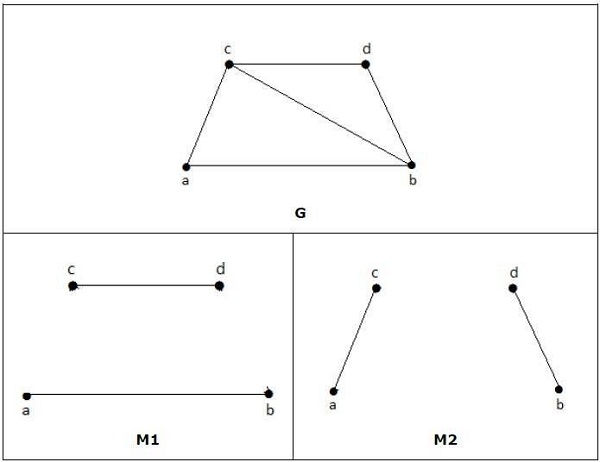
Note - Każde idealne dopasowanie wykresu jest jednocześnie maksymalnym dopasowaniem wykresu, ponieważ nie ma szans na dodanie jeszcze jednej krawędzi w idealnie dopasowanym wykresie.

Maksymalne dopasowanie wykresu nie musi być idealne. Jeśli wykres „G” ma idealne dopasowanie, to liczba wierzchołków | V (G) | jest równa. Jeśli jest nieparzysty, to ostatni wierzchołek łączy się w parę z drugim wierzchołkiem i ostatecznie pozostaje pojedynczy wierzchołek, którego nie można sparować z żadnym innym wierzchołkiem, dla którego stopień wynosi zero. Wyraźnie narusza to zasadę idealnego dopasowania.

Example

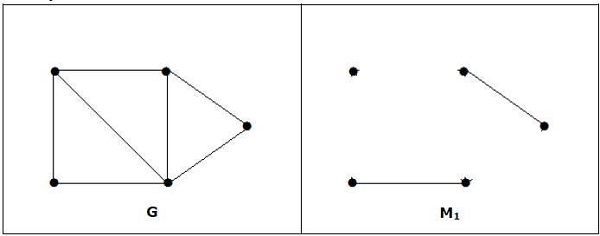
Note- Odwrotność powyższego stwierdzenia nie musi być prawdziwa. Jeśli G ma parzystą liczbę wierzchołków, to M1 nie musi być doskonały.

Example

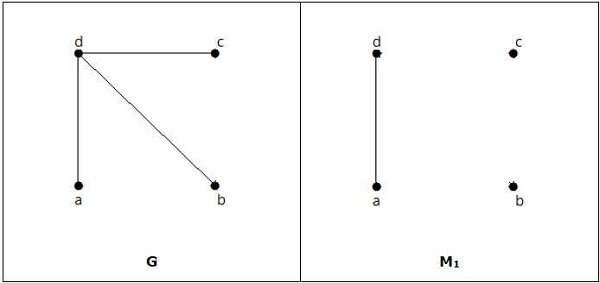
Pasuje, ale nie jest idealnie dopasowany, mimo że ma parzystą liczbę wierzchołków.

Zbiory niezależne są reprezentowane w zbiorach, w których

• nie powinno być any edges adjacent to each other. Nie powinno być żadnego wspólnego wierzchołka między dowolnymi dwiema krawędziami.

• nie powinno być any vertices adjacent to each other. Nie powinno być żadnej wspólnej krawędzi między dowolnymi dwoma wierzchołkami.

Niezależny zestaw linii

Niech „G” = (V, E) będzie wykresem. Podzbiór L z E nazywany jest niezależnym zestawem linii „G”, jeśli żadne dwie krawędzie w L nie sąsiadują ze sobą. Taki zestaw nazywany jest niezależnym zestawem linii.

Example

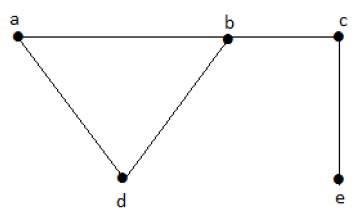
Rozważmy następujące podzbiory -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

W tym przykładzie podzbiory L2 i L3 wyraźnie nie są sąsiednimi krawędziami na danym wykresie. Są to niezależne zestawy linii. Jednak L1 nie jest niezależnym zestawem przewodów, ponieważ do wykonania niezależnego zestawu przewodów powinny być co najmniej dwie krawędzie.

Maksymalny zestaw niezależnych linii

O niezależnym zestawie linii mówi się, że jest to maksymalny niezależny zestaw linii wykresu „G”, jeśli żadna inna krawędź „G” nie może zostać dodana do „L”.

Example

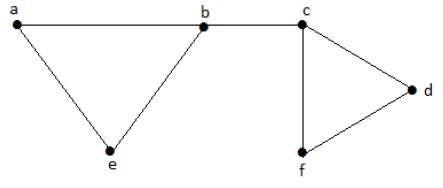
Rozważmy następujące podzbiory -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₂ and L₃ are maximal independent line sets/maximal matching. As for only these two subsets, there is no chance of adding any other edge which is not an adjacent. Hence these two subsets are considered as the maximal independent line sets.

Maximum Independent Line Set

A maximum independent line set of ‘G’ with maximum number of edges is called a maximum independent line set of ‘G’.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

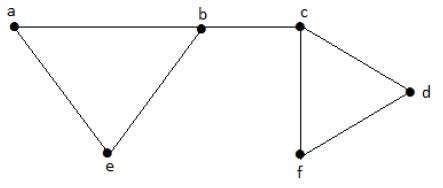
Let us consider the following subsets −

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L₃ is the maximum independent line set of G with maximum edges which are not the adjacent edges in graph and is denoted by β1 = 3.

Note − For any graph G with no isolated vertex,

α1 + β1 = number of vertices in a graph = |V|

Example

Line covering number of K_n/C_n/w_n,

$$\alpha 1 = \lceil\frac{n}{2}\rceil\begin{cases}\frac{n}{2}\:if\:n\:is\:even \\\frac{n+1}{2}\:if\:n\:is\:odd\end{cases}$$

Line independent number (Matching number) = β₁ = [n/2] α₁ + β₁ = n.

Independent Vertex Set

Let ‘G’ = (V, E) be a graph. A subset of ‘V’ is called an independent set of ‘G’ if no two vertices in ‘S’ are adjacent.

Example

Consider the following subsets from the above graphs −

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Clearly S₁ is not an independent vertex set, because for getting an independent vertex set, there should be at least two vertices in the from a graph. But here it is not that case. The subsets S₂, S₃, and S₄ are the independent vertex sets because there is no vertex that is adjacent to any one vertex from the subsets.

Maksymalny zestaw niezależnych wierzchołków

Niech „G” będzie grafem, wtedy mówi się, że niezależny zbiór wierzchołków „G” jest maksymalny, jeśli żaden inny wierzchołek „G” nie może zostać dodany do „S”.

Example

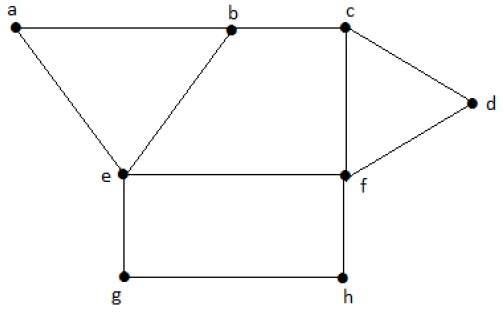
Rozważ następujące podzbiory z powyższych wykresów.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ i S ₃ to maksymalne niezależne zbiory wierzchołków „G”. W S ₁ i S ₄ możemy dodać inne wierzchołki; ale w S ₂ i S ₃ nie możemy dodać żadnego innego wierzchołka.

Maksymalny zestaw niezależnych wierzchołków

Maksymalny zbiór niezależnych wierzchołków „G” z maksymalną liczbą wierzchołków nazywany jest maksymalnym zestawem niezależnych wierzchołków.

Example

Rozważ następujące podzbiory z powyższego wykresu -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Tylko S ₃ to maksymalny zbiór niezależnych wierzchołków, ponieważ obejmuje największą liczbę wierzchołków. Liczba wierzchołków w maksymalnym niezależnym zbiorze wierzchołków „G” nazywana jest liczbą niezależnych wierzchołków G (β ₂ ).

Example

Dla całego wykresu K _n ,

Liczba pokrywająca wierzchołek = α ₂ = n − 1

Liczba niezależna od wierzchołków = β ₂ = 1

Masz α ₂ + β ₂ = n

Na pełnym wykresie każdy wierzchołek sąsiaduje z pozostałymi (n - 1) wierzchołkami. Dlatego maksymalny niezależny zbiór K _n zawiera tylko jeden wierzchołek.

Dlatego β ₂ = 1

i α ₂ = | v | - β ₂ = n-1

Note - Dla dowolnego wykresu „G” = (V, E)

• α ₂ + β ₂ = | v |
• Jeśli 'S' jest niezależnym zbiorem wierzchołków 'G', to (V - S) jest pokryciem wierzchołków G.

Kolorowanie wykresu to nic innego jak prosty sposób oznaczania komponentów wykresu, takich jak wierzchołki, krawędzie i regiony, w których występują pewne ograniczenia. Na wykresie żadne dwa sąsiednie wierzchołki, sąsiednie krawędzie ani sąsiednie regiony nie są pokolorowane minimalną liczbą kolorów. Ten numer nazywa sięchromatic number a wykres nazywa się a properly colored graph.

Podczas kolorowania wykresu ograniczeniami, które są ustawione na wykresie, są kolory, kolejność kolorowania, sposób nadawania kolorów itp. Kolorowanie jest nadawane wierzchołkowi lub określonemu obszarowi. Zatem wierzchołki lub regiony o tych samych kolorach tworzą niezależne zbiory.

Kolorowanie wierzchołków

Kolorowanie wierzchołków to przypisanie kolorów wierzchołkom wykresu „G” w taki sposób, że żadne dwa sąsiednie wierzchołki nie mają tego samego koloru. Mówiąc najprościej, żadne dwa wierzchołki krawędzi nie powinny być tego samego koloru.

Liczba chromatyczna

Minimalna liczba kolorów wymagana do kolorowania wierzchołków wykresu „G” nazywana jest liczbą chromatyczną G, oznaczoną przez X (G).

χ (G) = 1 wtedy i tylko wtedy, gdy „G” jest wykresem zerowym. Jeśli „G” nie jest grafem zerowym, to χ (G) ≥ 2.

Example

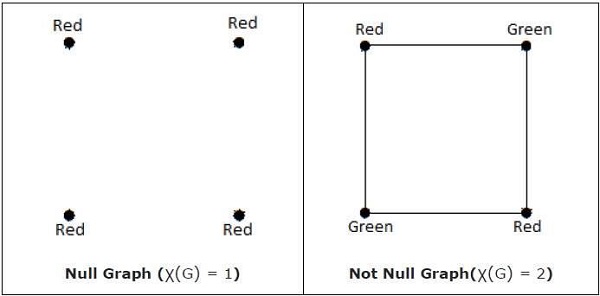
Note - O grafie „G” mówi się, że można go pokryć n, jeśli istnieje kolorystyka wierzchołków wykorzystująca najwyżej n kolorów, tj. X (G) ≤ n.

Kolorowanie regionu

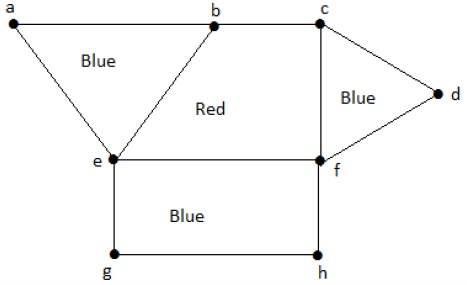
Kolorowanie regionów to przypisanie kolorów do obszarów wykresu planarnego, tak że żadne dwa sąsiednie regiony nie mają tego samego koloru. Mówi się, że dwa regiony sąsiadują ze sobą, jeśli mają wspólną krawędź.

Example

Spójrz na poniższy wykres. Regiony „aeb” i „befc” sąsiadują ze sobą, ponieważ między tymi dwoma regionami istnieje wspólna krawędź.

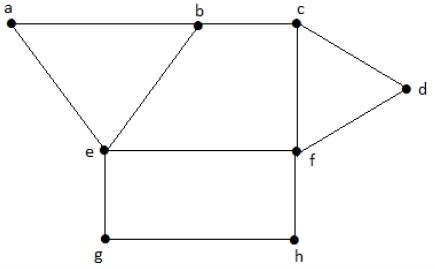
Podobnie inne regiony są również pokolorowane na podstawie przylegania. Ten wykres jest pokolorowany w następujący sposób -

Example

Liczba chromatyczna Kn wynosi

• n
• n–1
• [n/2]
• [n/2]

Rozważ ten przykład z K ₄ .

Na całym wykresie każdy wierzchołek sąsiaduje z pozostałymi (n - 1) wierzchołkami. Dlatego każdy wierzchołek wymaga nowego koloru. Stąd liczba chromatyczna K _n = n.

Zastosowania kolorowania wykresów

Kolorowanie grafów jest jednym z najważniejszych pojęć w teorii grafów. Jest używany w wielu aplikacjach informatycznych czasu rzeczywistego, takich jak -

• Clustering
• Eksploracja danych
• Przechwytywanie obrazu
• Segmentacja obrazu
• Networking
• Alokacja zasobów
• Planowanie procesów

Graf może istnieć w różnych formach, mając tę ​​samą liczbę wierzchołków, krawędzi, a także tę samą łączność krawędzi. Takie wykresy nazywane są grafami izomorficznymi. Zwróć uwagę, że opisujemy wykresy w tym rozdziale głównie w celu odniesienia się do nich i rozpoznania ich od siebie.

Grafy izomorficzne

O dwóch grafach G ₁ i G ₂ mówi się, że są izomorficzne, jeśli -

• Ich liczba komponentów (wierzchołków i krawędzi) jest taka sama.

• Ich łączność krawędziowa zostaje zachowana.

Note- Krótko mówiąc, z dwóch izomorficznych wykresów jeden jest poprawioną wersją drugiego. Graf bez etykiety można również traktować jako wykres izomorficzny.

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

Jeśli G ₁ ≡ G ₂ to -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

Sekwencje stopni G ₁ i G ₂ są takie same.

Jeśli wierzchołki {V ₁ , V ₂ , .. Vk} tworzą cykl o długości K w G ₁ , to wierzchołki {f (V ₁ ), f (V ₂ ),… f (Vk)} powinny tworzyć cykl długości K w G ₂ .

Wszystkie powyższe warunki są konieczne, aby grafy G ₁ i G ₂ były izomorficzne, ale nie są wystarczające do udowodnienia, że ​​wykresy są izomorficzne.

• (G ₁ ≡ G ₂ ) wtedy i tylko wtedy, gdy (G ₁ - ≡ G ₂ -), gdzie G ₁ i G ₂ są prostymi wykresami.

• (G ₁ ≡ G ₂ ), jeśli macierze sąsiedztwa G ₁ i G ₂ są takie same.

• (G ₁ ≡ G ₂ ) wtedy i tylko wtedy, gdy odpowiednie podgrafy G ₁ i G ₂ (otrzymane przez usunięcie niektórych wierzchołków w G1 i ich obrazy na grafie G ₂ ) są izomorficzne.

Example

Który z poniższych wykresów jest izomorficzny?

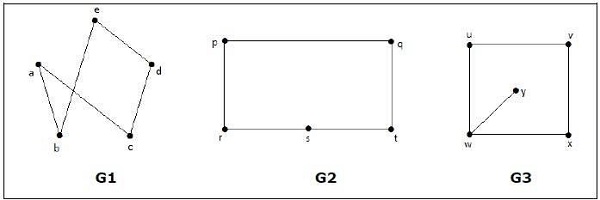
Na grafie G ₃ wierzchołek „w” ma tylko stopień 3, podczas gdy wszystkie inne wierzchołki grafu mają stopień 2. Stąd G3 nie jest izomorficzny z G ₁ ani G ₂ .

Biorąc uzupełnienia G ₁ i G ₂ , masz -

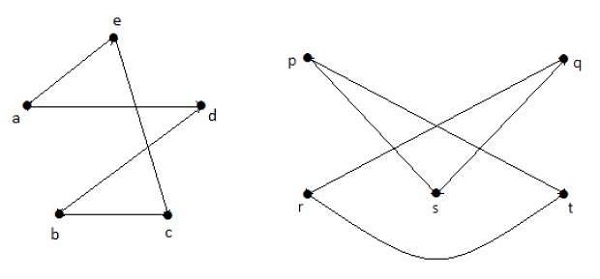
Tutaj (G ₁ - ≡ G ₂ -), stąd (G ₁ ≡ G ₂ ).

Wykresy planarne

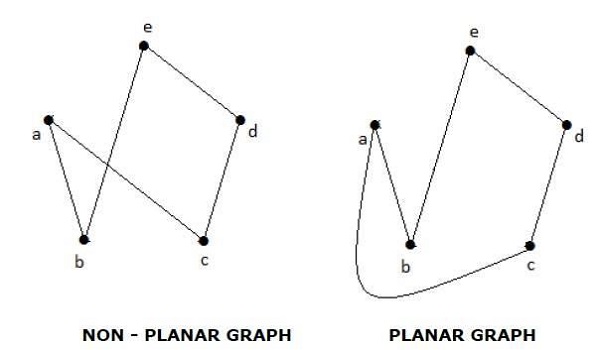
O grafie „G” mówi się, że jest płaski, jeśli można go narysować na płaszczyźnie lub kuli tak, że żadne dwie krawędzie nie przecinają się w punkcie innym niż wierzchołek.

Example

Regiony

Każdy planarny wykres dzieli płaszczyznę na połączone obszary zwane regionami.

Example

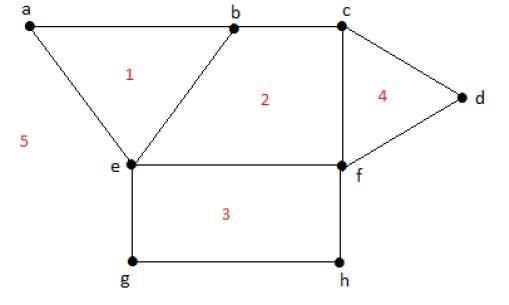
Stopień obszaru ograniczonego r = deg(r) = Liczba krawędzi otaczających regiony r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8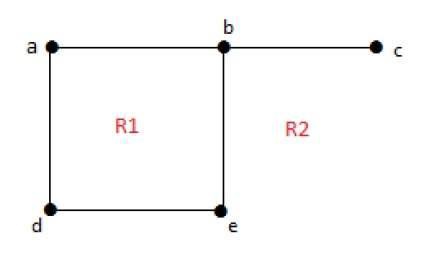

Stopień nieograniczonego regionu r = deg(r) = Liczba krawędzi otaczających regiony r.

deg(R1) = 4
deg(R2) = 6

Na grafach planarnych następujące właściwości są dobre -

Na wykresie planarnym z „n” wierzchołkami suma stopni wszystkich wierzchołków wynosi -

n Σ i = 1 stopień (V _i ) = 2 | E |

Według Sum of Degrees of Regions/ Twierdzenie, na wykresie planarnym z obszarami `` n '', suma stopni obszarów wynosi -

n Σ i = 1 st (ri) = 2 | E |

Na podstawie powyższego twierdzenia możesz wyciągnąć następujące wnioski -

Na wykresie planarnym

Jeśli stopień każdego regionu wynosi K, to suma stopni regionów wynosi -

K | R | = 2 | E |

Jeśli stopień każdego regionu wynosi co najmniej K (≥ K), to

K | R | ≤ 2 | E |

Jeśli stopień każdego regionu wynosi co najwyżej K (≤ K), to

K | R | ≥ 2 | E |

Note - Załóżmy, że wszystkie regiony mają ten sam stopień.

Według Euler’s Formulae na grafach planarnych,

Jeśli graf „G” jest połączoną płaszczyzną, to

| V | + | R | = | E | + 2

Jeśli wykres planarny z komponentami „K”, to

| V | + | R | = | E | + (Tys. + 1)

Gdzie, | V | jest liczbą wierzchołków, | E | jest liczbą krawędzi, a | R | to liczba regionów.

Nierówność krawędzi krawędzi

Jeśli „G” jest połączonym grafem planarnym ze stopniem każdego regionu co najmniej „K”, to

| E | ≤ k / (k-2) {| v | - 2}

Wiesz, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

Jeśli „G” jest prostym połączonym grafem planarnym, to

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Istnieje co najmniej jeden wierzchołek V • ∈ G taki, że deg (V) ≤ 5.

Jeśli „G” jest prostym połączonym grafem planarnym (z co najmniej 2 krawędziami) i bez trójkątów, to

|E| ≤ {2|V| – 4}

Twierdzenie Kuratowskiego

Graf „G” jest niepłaski wtedy i tylko wtedy, gdy „G” ma podgraf, który jest homeomorficzny względem K ₅ lub K _3,3 .

Homomorfizm

O dwóch grafach G ₁ i G ₂ mówi się, że są homomorficzne, jeśli każdy z tych grafów można uzyskać z tego samego grafu „G”, dzieląc niektóre krawędzie G większą liczbą wierzchołków. Spójrz na następujący przykład -

Podziel krawędź „rs” na dwie krawędzie, dodając jeden wierzchołek.

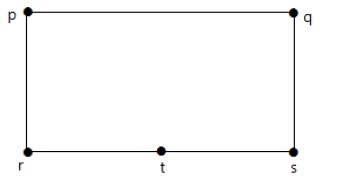
Wykresy pokazane poniżej są homomorficzne w stosunku do pierwszego wykresu.

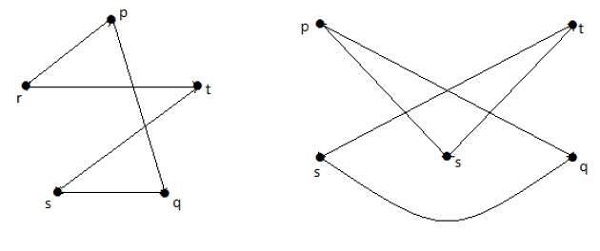
Jeśli G ₁ jest izomorficzna z G ₂ , to G jest homeomorficzna z G2, ale odwrotność nie musi być prawdą.

• Każdy wykres z 4 lub mniej wierzchołkami jest planarny.

• Każdy wykres z 8 lub mniej krawędziami jest planarny.

• Pełny wykres K _n jest planarny wtedy i tylko wtedy, gdy n ≤ 4.

• Pełny wykres dwudzielny K _{m, n} jest planarny wtedy i tylko wtedy, gdy m ≤ 2 lub n ≤ 2.

• Prosty graf niepłaski z minimalną liczbą wierzchołków jest grafem pełnym K ₅ .

• Prosty niepłaski wykres z minimalną liczbą krawędzi to K _{3, 3} .

Wykres wielościenny

Prosty połączony graf planarny nazywany jest grafem wielościennym, jeśli stopień każdego wierzchołka jest ≥ 3, tj. Deg (V) ≥ 3 ∀ V ∈ G.

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |

Po wykresie można przejść, jeśli można narysować ścieżkę między wszystkimi wierzchołkami bez odtwarzania tej samej ścieżki. W oparciu o tę ścieżkę istnieją pewne kategorie, takie jak ścieżka Eulera i obwód Eulera, które są opisane w tym rozdziale.

Ścieżka Eulera

Ścieżka Eulera zawiera każdą krawędź „G” dokładnie raz i każdy wierzchołek „G” co najmniej raz. Mówi się, że połączony wykres G jest przejezdny, jeśli zawiera ścieżkę Eulera.

Example

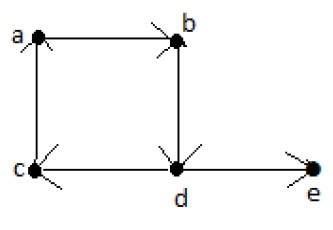
Ścieżka Eulera = dcabde.

Obwód Eulera

Na ścieżce Eulera, jeśli wierzchołek początkowy jest taki sam jak wierzchołek końcowy, wówczas nazywa się to obwodem Eulera.

Example

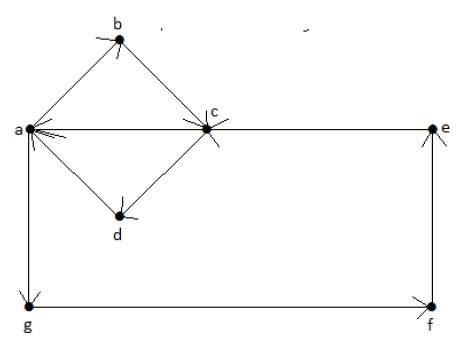
Euler’s Path = abcdagfeca.

Twierdzenie Eulera o obwodzie

Połączony graf „G” jest możliwy do przejścia wtedy i tylko wtedy, gdy liczba wierzchołków o nieparzystym stopniu w G wynosi dokładnie 2 lub 0. Połączony graf G może zawierać ścieżkę Eulera, ale nie obwód Eulera, jeśli ma dokładnie dwa wierzchołki z dziwny stopień.

Note - Ta ścieżka Eulera zaczyna się wierzchołkiem o nieparzystym stopniu i kończy się drugim wierzchołkiem o nieparzystym stopniu.

Example

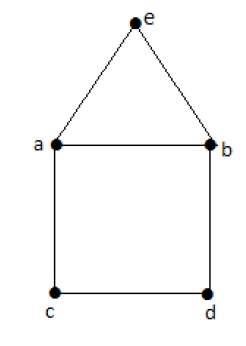
Euler’s Path- beabdca nie jest obwodem Eulera, ale jest ścieżką Eulera. Najwyraźniej ma dokładnie 2 nieparzyste wierzchołki.

Note - W połączonym grafie G, jeśli liczba wierzchołków o nieparzystym stopniu = 0, to obwód Eulera istnieje.

Wykres Hamiltona

O połączonym grafie G mówi się, że jest grafem hamiltonowskim, jeśli istnieje cykl, który zawiera wszystkie wierzchołki G.

Każdy cykl jest obwodem, ale obwód może zawierać wiele cykli. Taki cykl nazywa się aHamiltonian cycle G.

Ścieżka Hamiltona

Mówi się, że połączony graf jest hamiltonianem, jeśli zawiera każdy wierzchołek G dokładnie raz. Taka ścieżka nazywa sięHamiltonian path.

Example

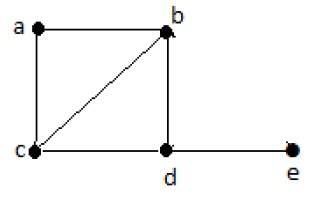
Hamiltonian Path- edbac.

Note

• Obwód Eulera zawiera każdą krawędź wykresu dokładnie raz.

• W cyklu hamiltonowskim niektóre krawędzie wykresu można pominąć.

Example

Spójrz na poniższy wykres -

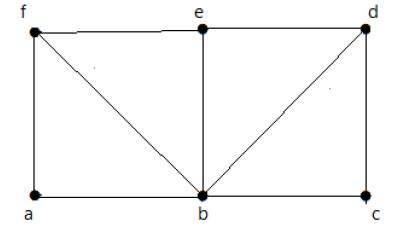
Dla wykresu pokazanego powyżej -

• Ścieżka Eulera istnieje - fałszywa

• Obwód Eulera istnieje - fałsz

• Istnieje cykl Hamiltona - prawda

• Ścieżka Hamiltona istnieje - prawda

G ma cztery wierzchołki o nieparzystym stopniu, dlatego nie można go przejść. Pomijając krawędzie wewnętrzne, wykres ma cykl Hamiltona przechodzący przez wszystkie wierzchołki.

W tym rozdziale omówimy kilka standardowych przykładów, aby zademonstrować koncepcje, które omówiliśmy już we wcześniejszych rozdziałach.

Przykład 1

Find the number of spanning trees in the following graph.

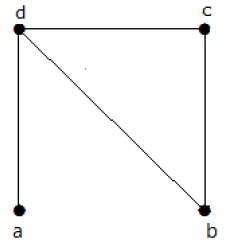
Rozwiązanie

Liczba drzew rozpinających uzyskana z powyższego wykresu wynosi 3. Są to:

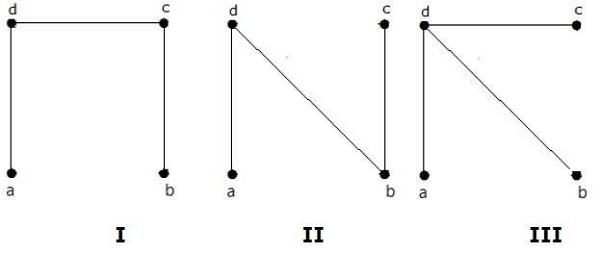
Te trzy są drzewami rozpinającymi dla danych wykresów. Tutaj wykresy I i II są ze sobą izomorficzne. Oczywiście liczba nieizomorficznych drzew rozpinających wynosi dwa.

Przykład 2

How many simple non-isomorphic graphs are possible with 3 vertices?

Rozwiązanie

Możliwe są 4 nieizomorficzne grafy z 3 wierzchołkami. Przedstawiono je poniżej.

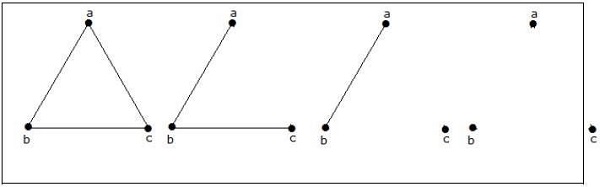
Przykład 3

Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.

Rozwiązanie

Twierdzenie o sumie stopni

20 Σ i = 1 st (Vi) = 2 | E |

20 (3) = 2 | E |

| E | = 30

Według wzoru Eulera,

| V | + | R | = | E | + 2

20+ | R | = 30 + 2

| R | = 12

Stąd liczba regionów wynosi 12.

Przykład 4

What is the chromatic number of complete graph K_n?

Rozwiązanie

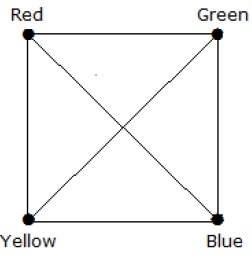
Na pełnym wykresie każdy wierzchołek sąsiaduje z pozostałymi (n – 1) wierzchołkami. Dlatego każdy wierzchołek wymaga nowego koloru. Stąd liczba chromatyczna K _n = n.

Przykład 5

What is the matching number for the following graph?

Rozwiązanie

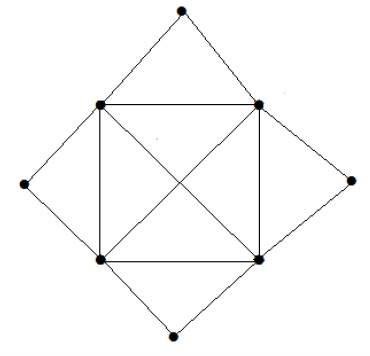
Liczba wierzchołków = 9

Możemy dopasować tylko 8 wierzchołków.

Pasująca liczba to 4.

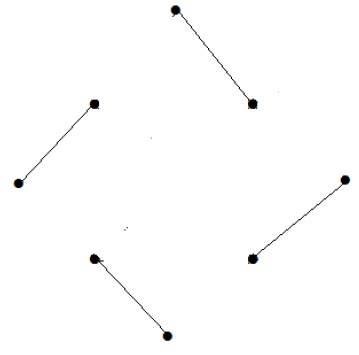
Przykład 6

What is the line covering number of for the following graph?

Rozwiązanie

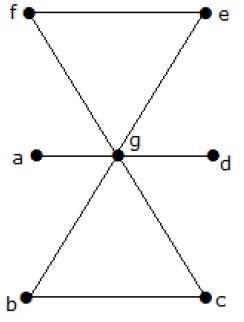
Liczba wierzchołków = | V | = n = 7

Numer pokrycia linii = (α ₁ ) ≥ [n / 2] = 3

α ₁ ≥ 3

Używając 3 krawędzi, możemy pokryć wszystkie wierzchołki.

Stąd numer obejmujący linię to 3.