Teoria grafów - izomorfizm

Graf może istnieć w różnych formach, mając tę ​​samą liczbę wierzchołków, krawędzi, a także tę samą łączność krawędzi. Takie wykresy nazywane są grafami izomorficznymi. Zwróć uwagę, że opisujemy wykresy w tym rozdziale głównie w celu odniesienia się do nich i rozpoznania ich od siebie.

Grafy izomorficzne

O dwóch grafach G ₁ i G ₂ mówi się, że są izomorficzne, jeśli -

• Ich liczba komponentów (wierzchołków i krawędzi) jest taka sama.

• Ich łączność krawędziowa zostaje zachowana.

Note- Krótko mówiąc, z dwóch izomorficznych wykresów jeden jest poprawioną wersją drugiego. Graf bez etykiety można również traktować jako wykres izomorficzny.

There exists a function ‘f’ from vertices of G1 to vertices of G2
   [f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.

Note

Jeśli G ₁ ≡ G ₂ to -

| V (G ₁ ) | = | V (G ₂ ) |

| E (G ₁ ) | = | E (G ₂ ) |

Sekwencje stopni G ₁ i G ₂ są takie same.

Jeśli wierzchołki {V ₁ , V ₂ , .. Vk} tworzą cykl o długości K w G ₁ , to wierzchołki {f (V ₁ ), f (V ₂ ),… f (Vk)} powinny tworzyć cykl długości K w G ₂ .

Wszystkie powyższe warunki są konieczne, aby grafy G ₁ i G ₂ były izomorficzne, ale nie są wystarczające do udowodnienia, że ​​wykresy są izomorficzne.

• (G ₁ ≡ G ₂ ) wtedy i tylko wtedy, gdy (G ₁ - ≡ G ₂ -), gdzie G ₁ i G ₂ są prostymi wykresami.

• (G ₁ ≡ G ₂ ), jeśli macierze sąsiedztwa G ₁ i G ₂ są takie same.

• (G ₁ ≡ G ₂ ) wtedy i tylko wtedy, gdy odpowiednie podgrafy G ₁ i G ₂ (otrzymane przez usunięcie niektórych wierzchołków w G1 i ich obrazy na grafie G ₂ ) są izomorficzne.

Example

Który z poniższych wykresów jest izomorficzny?

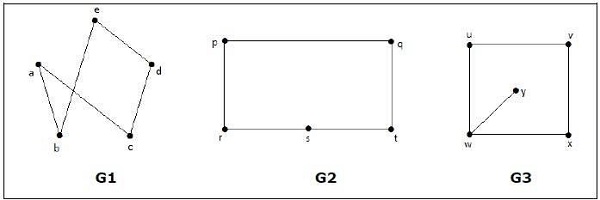
Na grafie G ₃ wierzchołek „w” ma tylko stopień 3, podczas gdy wszystkie inne wierzchołki grafu mają stopień 2. Stąd G3 nie jest izomorficzny z G ₁ ani G ₂ .

Biorąc uzupełnienia G ₁ i G ₂ , masz -

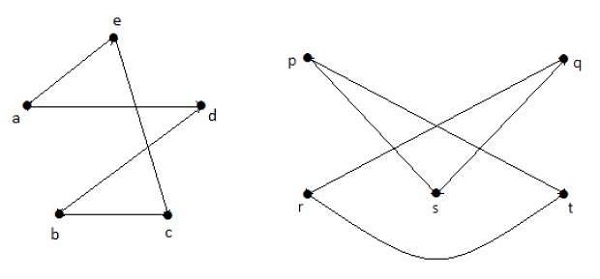
Tutaj (G ₁ - ≡ G ₂ -), stąd (G ₁ ≡ G ₂ ).

Wykresy planarne

O grafie „G” mówi się, że jest płaski, jeśli można go narysować na płaszczyźnie lub kuli tak, że żadne dwie krawędzie nie przecinają się w punkcie innym niż wierzchołek.

Example

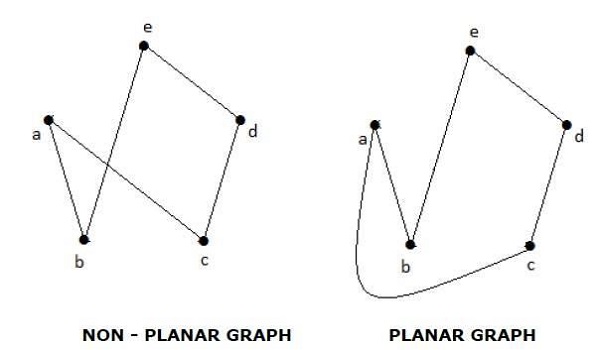
Regiony

Każdy planarny wykres dzieli płaszczyznę na połączone obszary zwane regionami.

Example

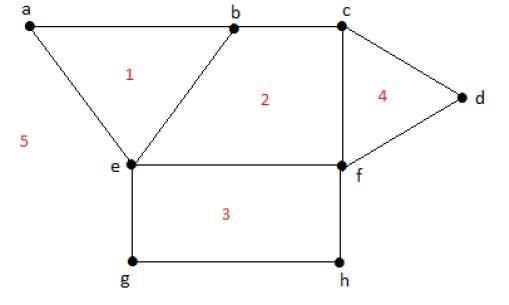
Stopień obszaru ograniczonego r = deg(r) = Liczba krawędzi otaczających regiony r.

deg(1) = 3
deg(2) = 4
deg(3) = 4

deg(4) = 3
deg(5) = 8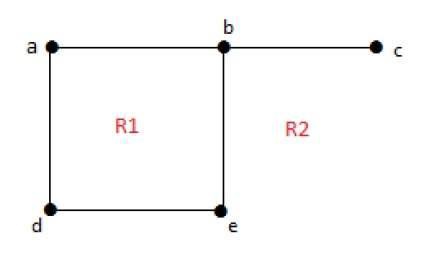

Stopień nieograniczonego regionu r = deg(r) = Liczba krawędzi otaczających regiony r.

deg(R1) = 4
deg(R2) = 6

Na grafach planarnych następujące właściwości są dobre -

Na wykresie planarnym z „n” wierzchołkami suma stopni wszystkich wierzchołków wynosi -

n Σ i = 1 stopień (V _i ) = 2 | E |

Według Sum of Degrees of Regions/ Twierdzenie, na wykresie planarnym z obszarami `` n '', suma stopni obszarów wynosi -

n Σ i = 1 st (ri) = 2 | E |

Na podstawie powyższego twierdzenia możesz wyciągnąć następujące wnioski -

Na wykresie planarnym

Jeśli stopień każdego regionu wynosi K, to suma stopni regionów wynosi -

K | R | = 2 | E |

Jeśli stopień każdego regionu wynosi co najmniej K (≥ K), to

K | R | ≤ 2 | E |

Jeśli stopień każdego regionu wynosi co najwyżej K (≤ K), to

K | R | ≥ 2 | E |

Note - Załóżmy, że wszystkie regiony mają ten sam stopień.

Według Euler’s Formulae na grafach planarnych,

Jeśli graf „G” jest połączoną płaszczyzną, to

| V | + | R | = | E | + 2

Jeśli wykres planarny z komponentami „K”, to

| V | + | R | = | E | + (Tys. + 1)

Gdzie, | V | jest liczbą wierzchołków, | E | jest liczbą krawędzi, a | R | to liczba regionów.

Nierówność krawędzi krawędzi

Jeśli „G” jest połączonym grafem planarnym ze stopniem każdego regionu co najmniej „K”, to

| E | ≤ k / (k-2) {| v | - 2}

Wiesz, | V | + | R | = | E | + 2

K. | R | ≤ 2 | E |

K (| E | - | V | + 2) ≤ 2 | E |

(K - 2) | E | ≤ K (| V | - 2)

| E | ≤ k / (k-2) {| v | - 2}

Jeśli „G” jest prostym połączonym grafem planarnym, to

|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4

Istnieje co najmniej jeden wierzchołek V • ∈ G taki, że deg (V) ≤ 5.

Jeśli „G” jest prostym połączonym grafem planarnym (z co najmniej 2 krawędziami) i bez trójkątów, to

|E| ≤ {2|V| – 4}

Twierdzenie Kuratowskiego

Graf „G” jest niepłaski wtedy i tylko wtedy, gdy „G” ma podgraf, który jest homeomorficzny względem K ₅ lub K _3,3 .

Homomorfizm

O dwóch grafach G ₁ i G ₂ mówi się, że są homomorficzne, jeśli każdy z tych grafów można uzyskać z tego samego grafu „G”, dzieląc niektóre krawędzie G większą liczbą wierzchołków. Spójrz na następujący przykład -

Podziel krawędź „rs” na dwie krawędzie, dodając jeden wierzchołek.

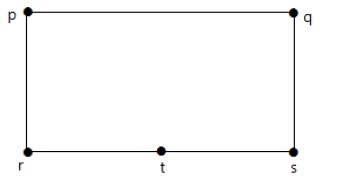
Wykresy pokazane poniżej są homomorficzne w stosunku do pierwszego wykresu.

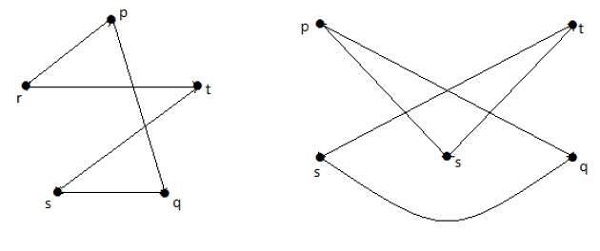
Jeśli G ₁ jest izomorficzna z G ₂ , to G jest homeomorficzna z G2, ale odwrotność nie musi być prawdą.

• Każdy wykres z 4 lub mniej wierzchołkami jest planarny.

• Każdy wykres z 8 lub mniej krawędziami jest planarny.

• Pełny wykres K _n jest planarny wtedy i tylko wtedy, gdy n ≤ 4.

• Pełny wykres dwudzielny K _{m, n} jest planarny wtedy i tylko wtedy, gdy m ≤ 2 lub n ≤ 2.

• Prosty graf niepłaski z minimalną liczbą wierzchołków jest grafem pełnym K ₅ .

• Prosty niepłaski wykres z minimalną liczbą krawędzi to K _{3, 3} .

Wykres wielościenny

Prosty połączony graf planarny nazywany jest grafem wielościennym, jeśli stopień każdego wierzchołka jest ≥ 3, tj. Deg (V) ≥ 3 ∀ V ∈ G.

• 3 | V | ≤ 2 | E |

• 3 | R | ≤ 2 | E |