Teoria grafów - zbiory niezależne

Zbiory niezależne są reprezentowane w zbiorach, w których

• nie powinno być any edges adjacent to each other. Pomiędzy dowolnymi dwoma krawędziami nie powinno być żadnego wspólnego wierzchołka.

• nie powinno być any vertices adjacent to each other. Między dwoma wierzchołkami nie powinno być żadnej wspólnej krawędzi.

Niezależny zestaw linii

Niech „G” = (V, E) będzie wykresem. Podzbiór L z E nazywany jest niezależnym zestawem linii „G”, jeśli żadne dwie krawędzie w L nie sąsiadują ze sobą. Taki zestaw nazywany jest niezależnym zestawem linii.

Example

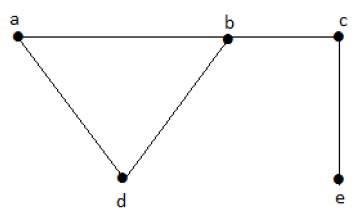
Rozważmy następujące podzbiory -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

W tym przykładzie podzbiory L2 i L3 wyraźnie nie są sąsiednimi krawędziami na danym wykresie. Są to niezależne zestawy linii. Jednak L1 nie jest niezależnym zestawem przewodów, ponieważ do wykonania niezależnego zestawu przewodów powinny być co najmniej dwie krawędzie.

Maksymalny zestaw niezależnych linii

O niezależnym zestawie linii mówi się, że jest to maksymalny niezależny zestaw linii wykresu „G”, jeśli żadna inna krawędź „G” nie może zostać dodana do „L”.

Example

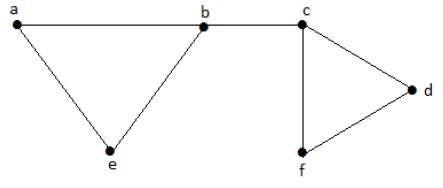
Rozważmy następujące podzbiory -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ i L ₃ to maksymalne niezależne zestawy linii / maksymalne dopasowanie. Jeśli chodzi tylko o te dwa podzbiory, nie ma szans na dodanie żadnej innej krawędzi, która nie jest sąsiadująca. Stąd te dwa podzbiory są uważane za maksymalne niezależne zestawy linii.

Maksymalny zestaw niezależnych linii

Maksymalny niezależny zestaw linii „G” z maksymalną liczbą krawędzi nazywany jest maksymalnym niezależnym zestawem linii „G”.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

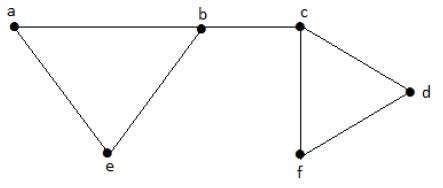
Rozważmy następujące podzbiory -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ jest maksymalnym niezależnym zestawem linii G z maksymalnymi krawędziami, które nie są krawędziami sąsiednimi na wykresie, i jest oznaczony przez β1 = 3.

Note - dla dowolnego grafu G bez izolowanego wierzchołka,

α1 + β1 = liczba wierzchołków w grafie = | V |

Example

Numer pokrycia linii K _n / C _n / w _n ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \: if \: n \: is \: even \\\ frac {n + 1} {2} \: if \: n \: is \: odd \ end {cases} $$

Liczba niezależna od linii (pasująca liczba) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Niezależny zestaw wierzchołków

Niech „G” = (V, E) będzie wykresem. Podzbiór „V” nazywany jest niezależnym zbiorem „G”, jeśli żadne dwa wierzchołki w „S” nie sąsiadują ze sobą.

Example

Rozważ następujące podzbiory z powyższych wykresów -

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Oczywiście S ₁ nie jest niezależnym zbiorem wierzchołków, ponieważ aby uzyskać niezależny zbiór wierzchołków, w grafie powinny znajdować się co najmniej dwa wierzchołki. Ale tutaj tak nie jest. Podzbiory S ₂ , S ₃ i S ₄ są niezależnymi zbiorami wierzchołków, ponieważ nie ma wierzchołka, który sąsiadowałby z żadnym wierzchołkiem z podzbiorów.

Maksymalny zestaw niezależnych wierzchołków

Niech „G” będzie grafem, wtedy mówi się, że niezależny zbiór wierzchołków „G” jest maksymalny, jeśli żaden inny wierzchołek „G” nie może zostać dodany do „S”.

Example

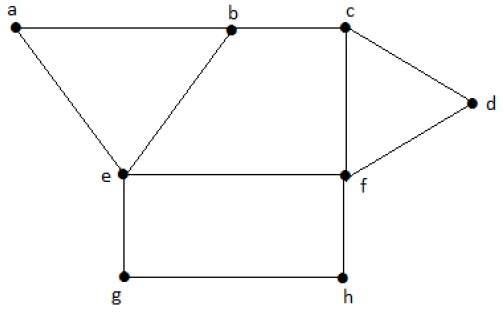
Rozważ następujące podzbiory z powyższych wykresów.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ i S ₃ to maksymalne niezależne zbiory wierzchołków „G”. W S ₁ i S ₄ możemy dodać inne wierzchołki; ale w S ₂ i S ₃ nie możemy dodać żadnego innego wierzchołka.

Maksymalny zestaw niezależnych wierzchołków

Maksymalny zbiór niezależnych wierzchołków „G” z maksymalną liczbą wierzchołków nazywany jest maksymalnym zestawem niezależnych wierzchołków.

Example

Rozważ następujące podzbiory z powyższego wykresu -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Tylko S ₃ to maksymalny zbiór niezależnych wierzchołków, ponieważ obejmuje największą liczbę wierzchołków. Liczba wierzchołków w maksymalnym niezależnym zbiorze wierzchołków „G” nazywana jest liczbą niezależnych wierzchołków G (β ₂ ).

Example

Dla całego wykresu K _n ,

Liczba pokrywająca wierzchołek = α ₂ = n − 1

Liczba niezależna od wierzchołków = β ₂ = 1

Masz α ₂ + β ₂ = n

Na pełnym wykresie każdy wierzchołek sąsiaduje z pozostałymi (n - 1) wierzchołkami. Dlatego maksymalny niezależny zbiór K _n zawiera tylko jeden wierzchołek.

Dlatego β ₂ = 1

i α ₂ = | v | - β ₂ = n-1

Note - Dla dowolnego wykresu „G” = (V, E)

• α ₂ + β ₂ = | v |
• Jeśli „S” jest niezależnym zbiorem wierzchołków „G”, to (V - S) jest pokryciem wierzchołka G.