Pole powierzchni sześcianu lub prostopadłościanu
W tej lekcji nauczymy się, jak obliczyć pole powierzchni pryzmatu prostokątnego i rozwiązać zadania dotyczące pola powierzchni pryzmatów prostokątnych.
ZA prismjest bryłą, która ma dwie równoległe ściany, które są przystającymi wielokątami na obu końcach. Te twarze tworzą podstawy pryzmatu. Nazwa pryzmatu pochodzi od kształtu jego podstawy. Pozostałe twarze mają kształt prostokątów. Nazywa się je bocznymi twarzami.
Poniższy diagram przedstawia prostokątny pryzmat.
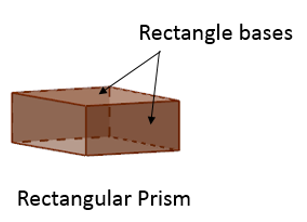
ZA right prism jest graniastosłupem, którego podstawy są prostopadłe do powierzchni bocznych.
Plik surface area pryzmatu to całkowita powierzchnia wszystkich jego zewnętrznych ścian.
To calculate the surface area of a rectangular prism
Obliczamy pole każdej z sześciu ścian pryzmatu.
Następnie sumujemy wszystkie obszary, aby uzyskać całkowitą powierzchnię.
Formula to find the surface area of a prism
Pole powierzchni graniastosłupa = 2 × pole powierzchni podstawy + obwód podstawy × wysokość graniastosłupa
Formula to find the surface area of a rectangular prism
Pole powierzchni prostopadłościanu = 2 (l × w + w × h + l × h)
Gdzie,
l - długość pryzmatu
w - szerokość pryzmatu i
h - wysokość pryzmatu
Znajdź pole powierzchni danego pryzmatu prostokątnego w cm kwadratowych.
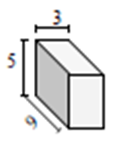
Rozwiązanie
Step 1:
Pole powierzchni prostokątnego graniastosłupa = 2 (l × w + w × h + 1 × h); l = 3 cm; w = 5 cm; h = 9 cm
Step 2:
Pole powierzchni danego pryzmatu = 2 (3 × 5 + 3 × 9 + 9 × 5)
= 2 (15 + 27 + 45)
= 174 cm kwadratowych
Znajdź pole powierzchni danego pryzmatu prostokątnego w cm kwadratowych.
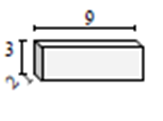
Rozwiązanie
Step 1:
Pole powierzchni prostokątnego graniastosłupa = 2 (l × w + w × h + l × h); l = 9 cm; w = 3 cm; h = 2 cm
Step 2:
Pole powierzchni danego pryzmatu = 2 (9 × 3 + 9 × 2 + 3 × 2)
= 2 (27 + 18 + 6)
= 102 cm kwadratowe