Użycie siatki do wyznaczenia pola powierzchni trójkątnego pryzmatu
W tej lekcji do wyznaczenia pola powierzchni trójkątnego pryzmatu używamy sieci trójkątnego pryzmatu.
Plik net bryły figury powstaje, gdy bryła jest rozłożona wzdłuż jej krawędzi, a jej ściany są ułożone we wzór w dwóch wymiarach.
Siatki trójkątnych graniastosłupów składają się z prostokątów i trójkątów.
Using a net to find the surface area of a rectangular prism
Znalezienie pól każdego z prostokątów i trójkątów sieci trójkątnego graniastosłupa i zsumowanie tych obszarów daje pole powierzchni lub całkowite pole powierzchni trójkątnego graniastosłupa.
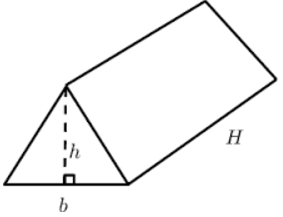
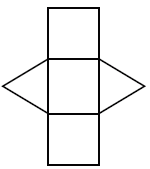
Na przykład, niech nogi trójkąta prostokątnego będącego podstawą trójkątnego graniastosłupa mają 3 i 4 jednostki, a wysokość pryzmatu 10 jednostek. Z sieci widzimy, że istnieją dwie przystające trójkątne ściany i trzy prostokątne ściany, których obszary są następujące. 6 jednostek kwadratowych i (3 + 4 + 5) 10 = 120 jednostek kwadratowych. Pole powierzchni pryzmatu = 2 (6) + 120 = 132 jednostki kwadratowe.
Surface Area of a Triangular Prism using Nets
Znajdź pole powierzchni następującego trójkątnego pryzmatu za pomocą siatki.

Rozwiązanie
Step 1:
Używając siatki, pole powierzchni trójkątnego pryzmatu
Boki podstawy trójkąta
a = 13 mm; b = 13 mm; c = 10 mm; wysokość h = 14mm
Obszar trójkąta = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{18\left ( 18-13 \right )\left ( 18-13 \right )\left ( 18-10 \right )}$
= 60 mm kwadratowych
Step 2:
Pole powierzchni pryzmatu = 2 pole trójkąta + h (a + b + c)
= 2 (60) + (13 + 13 + 10) 14
= 120 + 504
= 624 cm kwadratowych
Znajdź pole powierzchni następującego trójkątnego pryzmatu za pomocą siatki.

Rozwiązanie
Step 1:
Używając siatki, pole powierzchni trójkątnego pryzmatu
Boki podstawy trójkąta
a = 21 cm; b = 28 cm; c = 35 cm; wysokość h = 14cm
Obszar trójkąta = $\sqrt{s\left ( s-a \right )\left ( s-b \right )\left ( s-c \right )}$
= $\sqrt{42\left ( 42-21 \right )\left ( 42-28 \right )\left ( 42-35 \right )}$
= 294
Step 2:
Pole powierzchni pryzmatu = 2 pole trójkąta + h (a + b + c)
= 2 (294) + (21 + 28 + 35) 14
= 588 + 1176
= 1764 cm kwadratowych