Kombinacyjne obwody logiczne MOS

Obwody lub bramki logiczne kombinacyjne, które wykonują operacje boolowskie na wielu zmiennych wejściowych i określają wyjścia jako funkcje boolowskie wejść, są podstawowymi elementami składowymi wszystkich systemów cyfrowych. Przeanalizujemy proste konfiguracje obwodów, takie jak dwuwejściowe bramki NAND i NOR, a następnie rozszerzymy naszą analizę o bardziej ogólne przypadki struktur obwodów z wieloma wejściami.

Następnie obwody logiczne CMOS zostaną przedstawione w podobny sposób. Podkreślimy podobieństwa i różnice między logiką zubożenia nMOS a układami logicznymi CMOS i wskażemy na przykładach zalety bramek CMOS. W swojej najbardziej ogólnej postaci, kombinacyjny obwód logiczny lub bramka wykonująca funkcję boolowską można przedstawić jako system z wieloma wejściami i jednym wyjściem, jak pokazano na rysunku.

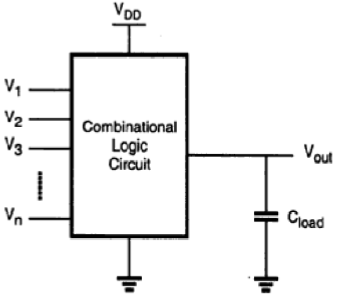
Napięcia węzłów w odniesieniu do potencjału ziemi reprezentują wszystkie zmienne wejściowe. Stosując konwencję logiki dodatniej, wartość boolowska (lub logiczna) „1” może być reprezentowana przez wysokie napięcie VDD, a wartość boolowska (lub logiczna) „0” może być reprezentowana przez niskie napięcie równe 0. Wyjście węzeł jest obciążony pojemnością C _L , która reprezentuje połączone pojemności urządzenia pasożytniczego w obwodzie.

Obwody logiczne CMOS

CMOS Podwójna bramka NOR

Obwód składa się z połączonej równolegle n-sieci i połączonej szeregowo, uzupełniającej sieci typu p-net. Napięcia wejściowe V _X i V _Y są przykładane do bramek jednego tranzystora nMOS i jednego tranzystora pMOS.

Kiedy jedno lub oba wejścia są wysokie, tj. Gdy n-net tworzy ścieżkę przewodzącą między węzłem wyjściowym a ziemią, p-net jest odcinany. Jeżeli oba napięcia wejściowe są niskie, tj. N-net jest odcięty, wówczas p-net tworzy ścieżkę przewodzącą między węzłem wyjściowym a napięciem zasilającym.

Dla dowolnej kombinacji wejść komplementarna struktura obwodu jest taka, że wyjście jest podłączone albo do V _DD albo do masy poprzez ścieżkę o niskiej rezystancji, a ścieżka prądu stałego między V _DD a masą nie jest ustanowiona dla żadnej kombinacji wejść. Napięcie wyjściowe CMOS, dwie wejściowe bramki NOR otrzymają niskie napięcie logiczne V _OL = 0 i wysokie napięcie logiczne V _OH = V _DD . Równanie progu przełączania napięcia V _th jest podane wzorem

$$ V_ {th} \ left (NOR2 \ right) = \ frac {V_ {T, n} + \ frac {1} {2} \ sqrt {\ frac {k_ {p}} {k_ {n}} \ left (V_ {DD} - \ left | V_ {T, p} \ right | \ right)}} {1+ \ frac {1} {2} \ sqrt {\ frac {k_ {p}} {k_ {n }}}} $$

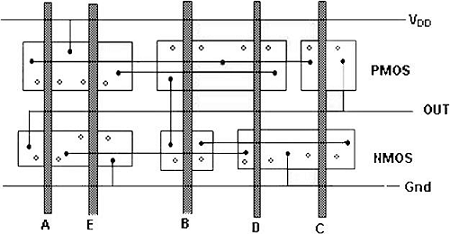
Układ 2-wejściowej bramki NOR CMOS

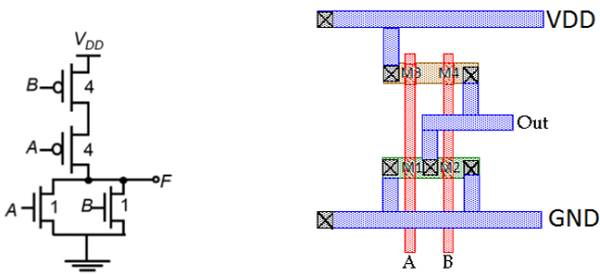
Rysunek przedstawia przykładowy układ 2-wejściowej bramki NOR CMOS, wykorzystującej jednowarstwowy metal i jednowarstwowy polikrzem. Cechy tego układu to -

Pojedyncze pionowe polilinie dla każdego wejścia
Pojedyncze aktywne kształty odpowiednio dla urządzeń N i P.
Metalowe autobusy jeżdżące poziomo

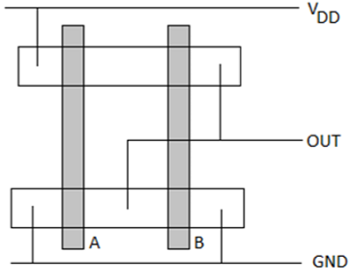
Schemat stick dla bramki CMOS N0R2 pokazano na poniższym rysunku; który odpowiada bezpośrednio układowi, ale nie zawiera informacji W i L. Obszary dyfuzyjne są przedstawione prostokątami, metalowe połączenia oraz ciągłe linie i okręgi reprezentują odpowiednio kontakty, a kreskowane paski przedstawiają kolumny polikrzemu. Diagram prętowy jest przydatny do planowania optymalnej topologii układu.

Podwójna bramka NAND CMOS

Schemat obwodu dwóch wejściowych bramek CMOS NAND przedstawiono na poniższym rysunku.

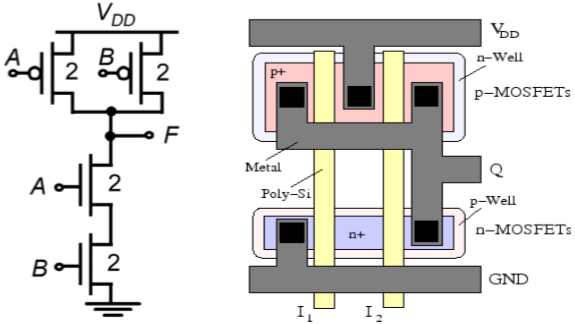
Zasada działania obwodu jest dokładnie podwójna w stosunku do operacji CMOS z dwoma wejściami NOR. Sieć n - składająca się z dwóch połączonych szeregowo tranzystorów nMOS tworzy ścieżkę przewodzącą między węzłem wyjściowym a uziemieniem, jeśli oba napięcia wejściowe są logicznie wysokie. Oba równolegle połączone tranzystory pMOS w sieci p-net będą wyłączone.

Dla wszystkich innych kombinacji wejść jeden lub oba tranzystory pMOS zostaną włączone, podczas gdy p-net jest odcięty, tworząc w ten sposób ścieżkę prądową między węzłem wyjściowym a napięciem zasilania. Próg przełączania dla tej bramki uzyskuje się jako -

$$ V_ {th} \ left (NAND2 \ right) = \ frac {V_ {T, n} +2 \ sqrt {\ frac {k_ {p}} {k_ {n}} \ left (V_ {DD} - \ left | V_ {T, p} \ right | \ right)}} {1 + 2 \ sqrt {\ frac {k_ {p}} {k_ {n}}}} $$

Cechy tego układu są następujące -

Pojedyncze linie polikrzemu dla wejść biegną pionowo w obu regionach aktywnych N i P.
Pojedyncze aktywne kształty są używane do budowy zarówno urządzeń nMOS, jak i obu urządzeń pMOS.
Magistrala zasilania przebiega poziomo w górnej i dolnej części układu.
Przewody wyjściowe biegną poziomo, co ułatwia podłączenie do sąsiedniego obwodu.

Złożone obwody logiczne

Złożona brama logiczna obciążenia NMOS

Aby zrealizować złożone funkcje wielu zmiennych wejściowych, podstawowe struktury obwodów i zasady projektowania opracowane dla NOR i NAND można rozszerzyć na złożone bramki logiczne. Możliwość realizacji złożonych funkcji logicznych przy użyciu niewielkiej liczby tranzystorów jest jedną z najbardziej atrakcyjnych cech układów logicznych nMOS i CMOS. Jako przykład rozważmy następującą funkcję logiczną.

$$ \ overline {Z = P \ left (S + T \ right) + QR} $$

Złożona bramka logiczna nMOS zubażania-obciążenia używana do realizacji tej funkcji jest pokazana na rysunku. Na tym rysunku lewa gałąź sterownika nMOS, składająca się z trzech tranzystorów sterownika, jest wykorzystywana do realizacji funkcji logicznej P (S + T), podczas gdy gałąź po prawej stronie pełni funkcję QR. Łącząc równolegle dwie gałęzie i umieszczając tranzystor obciążający między węzłem wyjściowym a napięciem zasilaniaV_DD,otrzymujemy daną funkcję złożoną. Każda zmienna wejściowa jest przypisana tylko do jednego sterownika.

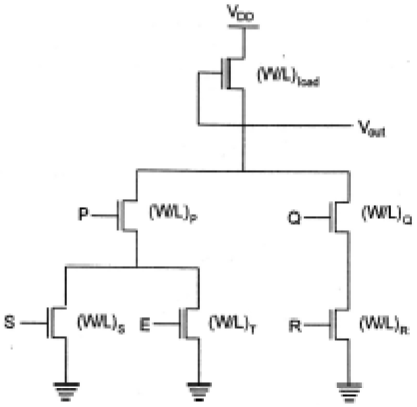
Inspekcja topologii obwodu daje proste zasady projektowania sieci rozwijanej -

Operacje OR są wykonywane przez sterowniki połączone równolegle.
Operacje AND są wykonywane przez sterowniki połączone szeregowo.
Odwrócenie jest zapewnione przez naturę działania obwodu MOS.

Jeśli wszystkie zmienne wejściowe mają wysoki stan logiczny w obwodzie realizującym funkcję, odpowiedni sterownik (W/L) stosunek sieci pull-down składającej się z pięciu tranzystorów nMOS wynosi

$$ \ frac {W} {L} = \ frac {1} {\ frac {1} {\ left (W / L \ right) Q} + \ frac {1} {\ left (W / L \ right) R}} + \ frac {1} {\ frac {1} {\ left (W / L \ right) P} + \ frac {1} {\ left (W / L \ right) S + \ left (W / L \ right) Q}} $$

Złożone bramki logiczne CMOS

Realizacja sieci n-net lub sieci typu pull-down opiera się na tych samych podstawowych zasadach projektowych, które zostały zbadane dla złożonej bramki logicznej nMOS ze zubożeniem obciążenia. Sieć podciągająca pMOS musi być podwójną siecią n-net.

Oznacza to, że wszystkie połączenia równoległe w sieci nMOS będą odpowiadać połączeniom szeregowym w sieci pMOS, a wszystkie połączenia szeregowe w sieci nMOS odpowiadają połączeniom równoległym w sieci pMOS. Rysunek przedstawia prostą konstrukcję wykresu dual p-net (pull-up) z wykresu n-net (pull-down).

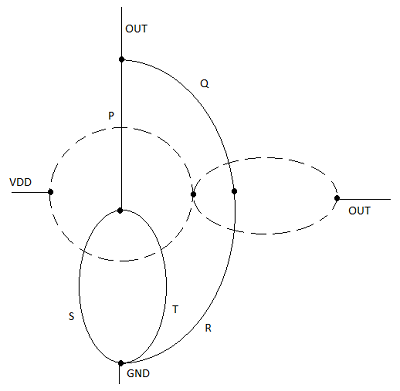
Każdy tranzystor sterownika w sieci rozwijanej jest pokazany jako ai, a każdy węzeł jest pokazany jako wierzchołek na wykresie rozwijanym. Następnie w każdym ograniczonym obszarze na wykresie ściągania tworzony jest nowy wierzchołek, a sąsiednie wierzchołki są połączone krawędziami, które przecinają każdą krawędź na wykresie rozwijanym tylko raz. Ten nowy wykres przedstawia sieć podciągającą.

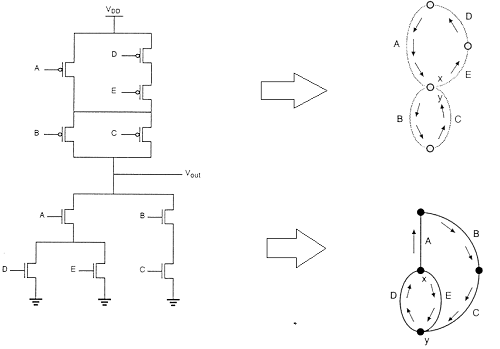
Technika układu przy użyciu metody wykresu Eulera

Rysunek pokazuje implementację złożonej funkcji CMOS i jej diagram w postaci styków z dowolną kolejnością bramek, co daje bardzo nieoptymalny układ dla bramki CMOS.

W tym przypadku separacja między kolumnami polikrzemu musi umożliwiać separację dyfuzyjno-dyfuzyjną pomiędzy nimi. To z pewnością pochłania znaczną ilość dodatkowej powierzchni krzemu.

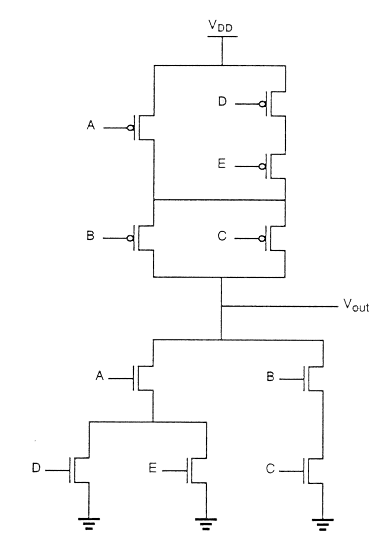
Korzystając ze ścieżki Eulera możemy uzyskać optymalny układ. Ścieżka Eulera jest definiowana jako nieprzerwana ścieżka, która przechodzi przez każdą krawędź (gałąź) wykresu dokładnie raz. Znajdź ścieżkę Eulera zarówno na rozwijanym wykresie drzewa, jak i na rozwijanym wykresie drzewa z identyczną kolejnością wejść.