Projekt VLSI - tranzystor MOS
Komplementarna technologia MOSFET (CMOS) jest obecnie szeroko stosowana do tworzenia obwodów w licznych i zróżnicowanych zastosowaniach. Dzisiejsze komputery, procesory i telefony komórkowe wykorzystują CMOS ze względu na kilka kluczowych zalet. CMOS oferuje niskie rozpraszanie mocy, stosunkowo dużą prędkość, wysokie marginesy szumów w obu stanach i będzie działać w szerokim zakresie napięć źródłowych i wejściowych (pod warunkiem, że napięcie źródła jest stałe)
W przypadku procesów, które omówimy, typem dostępnego tranzystora jest tranzystor polowy typu metal-tlenek-półprzewodnik (MOSFET). Powstają te tranzystoryas a ‘sandwich’składający się z warstwy półprzewodnika, zwykle plastra lub płytki z pojedynczego kryształu krzemu; warstwa dwutlenku krzemu (tlenek) i warstwa metalu.
Struktura MOSFET-u
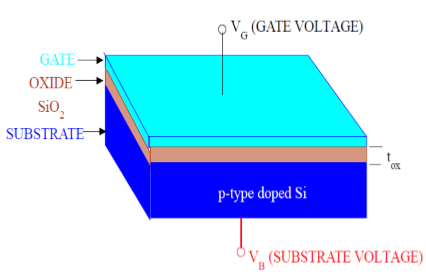
Jak pokazano na rysunku, struktura MOS zawiera trzy warstwy -
The Metal Gate Electrode
The Insulating Oxide Layer (SiO2)
P – type Semiconductor (Substrate)
Struktura MOS tworzy kondensator, a bramka i podłoże są jak dwie płytki i warstwa tlenku jako materiał dielektryczny. Grubość materiału dielektrycznego (SiO 2 ) wynosi zwykle od 10 nm do 50 nm. Koncentracją i rozkładem nośników w podłożu można manipulować za pomocą zewnętrznego napięcia przyłożonego do bramki i końcówki podłoża. Teraz, aby zrozumieć strukturę MOS, najpierw rozważ podstawowe właściwości elektryczne podłoża półprzewodnikowego typu P.
Koncentracja nośnika w materiale półprzewodnikowym jest zawsze zgodna z Mass Action Law. Prawo zbiorowych działań jest podane przez -
$$ np = n_ {i} ^ {2} $$
Gdzie,
n to stężenie nośników elektronów
p jest nośnikiem koncentracji otworów
ni jest wewnętrznym stężeniem nośnika krzemu
Załóżmy teraz, że podłoże jest równomiernie domieszkowany akceptor (boru) stężenie N A . Zatem stężenie elektronów i dziur w podłożu typu p wynosi
$$ n_ {po} = \ frac {n_ {i} ^ {2}} {N_ {A}} $$
$$ p_ {po} = N_ {A} $$
Tutaj koncentracja dopingu NAjest (10 15 do 10 16 cm -3 ) większe niż wewnętrzne stężenie ni. Teraz, aby zrozumieć strukturę MOS, rozważ diagram poziomów energetycznych podłoża krzemowego typu p.
Jak pokazano na rysunku, przerwa wzbroniona między pasmem przewodnictwa a pasmem falbaniowym wynosi 1,1 eV. Tutaj potencjał Fermiego Φ F jest różnicą między wewnętrznym poziomem Fermiego (E i ) a poziomem Fermiego (E FP ).
Gdzie poziom Fermiego E F zależy od stężenia domieszki. Potencjał Fermiego Φ F jest różnicą między wewnętrznym poziomem Fermiego (E i ) a poziomem Fermiego (E FP ).
Matematycznie,
$$ \ Phi_ {Fp} = \ frac {E_ {F} -E_ {i}} {q} $$
Potencjalna różnica między pasmem przewodnictwa a wolną przestrzenią nazywa się powinowactwem elektronowym i jest oznaczona przez qx.
Tak więc energia potrzebna do przejścia elektronu z poziomu Fermiego do wolnej przestrzeni nazywana jest funkcją pracy (qΦ S ) i jest wyrażona przez
$$ q \ Phi _ {s} = (E_ {c} -E_ {F}) + qx $$
Poniższy rysunek przedstawia schemat pasm energetycznych komponentów tworzących MOS.
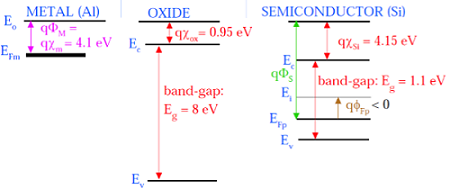
Jak pokazano na powyższym rysunku, izolacyjna warstwa SiO 2 ma dużą energetyczną przerwę energetyczną 8eV, a funkcja pracy wynosi 0,95 eV. Metalowa brama ma funkcję pracy 4,1eV. Tutaj funkcje robocze są różne, więc spowoduje spadek napięcia w systemie MOS. Poniższy rysunek przedstawia schemat połączonego pasma energii systemu MOS.
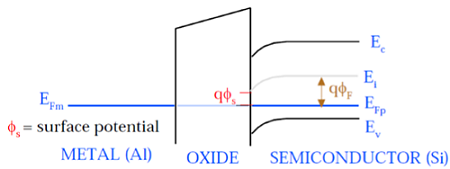
Jak pokazano na tym rysunku, poziom potencjału fermiego metalowej bramki i półprzewodnika (Si) ma ten sam potencjał. Potencjał Fermiego na powierzchni nazywany jest potencjałem powierzchniowym Φ S i jest mniejszy niż potencjał Fermiego Φ F pod względem wielkości.
Działanie MOSFET-u
MOSFET składa się z kondensatora MOS z dwoma złączami pn umieszczonymi w pobliżu obszaru kanału, a obszar ten jest kontrolowany napięciem bramki. Aby oba złącza pn były spolaryzowane odwrotnie, potencjał podłoża jest utrzymywany poniżej potencjału pozostałych trzech końcówek.
Jeśli napięcie bramki wzrośnie powyżej napięcia progowego (V GS > V TO ), na powierzchni utworzy się warstwa inwersyjna, a pomiędzy źródłem a drenem utworzy się kanał typu n. Ten kanał typu n przenosi prąd drenu zgodnie z wartością V DS .
Dla różnych wartości V DS , MOSFET może działać w różnych regionach, jak wyjaśniono poniżej.
Region liniowy
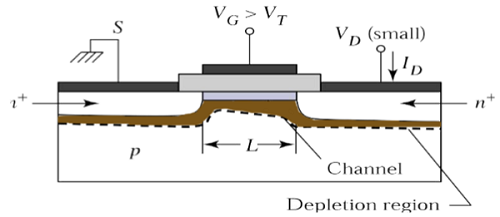
Przy V DS = 0, równowaga termiczna istnieje w obszarze odwróconego kanału i prąd drenu I D = 0. Teraz, jeśli zostanie przyłożone małe napięcie drenu, V DS > 0, prąd drenu proporcjonalny do V DS zacznie płynąć od źródła do spuścić przez kanał.
Kanał zapewnia ciągłą ścieżkę przepływu prądu od źródła do drenu. Ten tryb działania nosi nazwęlinear region. Widok przekroju n-kanałowego tranzystora MOSFET działającego w obszarze liniowym pokazano na poniższym rysunku.
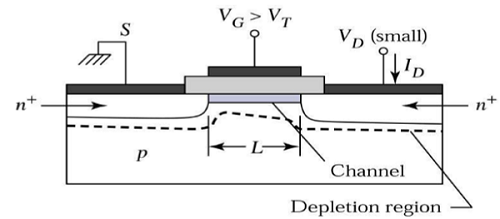
Na skraju regionu nasycenia
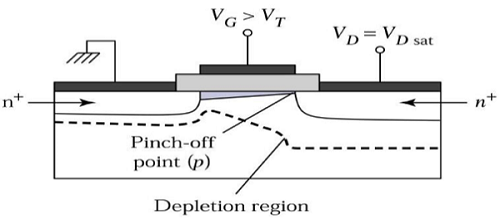
Teraz, jeśli V DS wzrośnie, ładunki w kanale i głębokość kanału zmniejszają się pod koniec odpływu. Dla V DS = V DSAT ładunki w kanale są redukowane do zera, co jest tzwpinch – off point. Widok przekroju n-kanałowego tranzystora MOSFET pracującego na skraju obszaru nasycenia pokazano na poniższym rysunku.
Region nasycenia
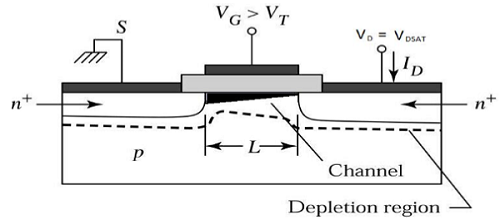
Dla V DS > V DSAT , zubożona powierzchnia tworzy się w pobliżu drenu, a poprzez zwiększenie napięcia drenu ten zubożony obszar rozciąga się do źródła.
Ten tryb działania nosi nazwę Saturation region. Elektrony docierające ze źródła do końca kanału wchodzą do obszaru wyczerpania drenu i przyspieszają w kierunku drenu w silnym polu elektrycznym.
Prąd MOSFET - Charakterystyka napięcia
Aby zrozumieć charakterystykę prądowo-napięciową tranzystora MOSFET, wykonuje się przybliżenie kanału. Bez tego przybliżenia trójwymiarowa analiza systemu MOS staje się złożona. PlikGradual Channel Approximation (GCA) dla charakterystyki prądowo-napięciowej zmniejszy problem analizy.
Stopniowe przybliżanie kanałów (GCA)
Rozważmy przekrój poprzeczny tranzystora MOSFET z kanałem n pracującym w trybie liniowym. Tutaj źródło i podłoże są połączone z ziemią. V S = V, B = 0. bramy - do - źródła (V GS ) i dren - do - źródła napięcia (V DS ) napięcia są parametrami zewnętrzne, które sterują odpływu prądu I D .
Napięcie V GS jest ustawione na napięcie większe niż napięcie progowe V TO , aby utworzyć kanał między źródłem a drenem. Jak pokazano na rysunku, kierunek x jest prostopadły do powierzchni, a kierunek y jest równoległy do powierzchni.
Tutaj y = 0 na końcu źródła, jak pokazano na rysunku. Napięcie kanału w odniesieniu do źródła jest reprezentowane przezVC(Y). Załóżmy, że napięcie progowe VTO jest stałe wzdłuż obszaru kanału, od y = 0 do y = L.Warunek brzegowy dla napięcia kanału V C wynosi -
$$ V_ {c} \ left (y = 0 \ right) = V_ {s} = 0 \, and \, V_ {c} \ left (y = L \ right) = V_ {DS} $$
Możemy też to założyć
$$ V_ {GS} \ geq V_ {TO} $$ i
$$ V_ {GD} = V_ {GS} -V_ {DS} \ geq V_ {TO} $$
Niech Q1 (y) będzie całkowitym ładunkiem ruchomych elektronów w powierzchniowej warstwie inwersyjnej. Ten ładunek elektronu można wyrazić jako -
$$ Q1 (y) = - C_ {ox}. [V_ {GS} -V_ {C (Y)} - V_ {TO}] $$
Poniższy rysunek przedstawia geometrię przestrzenną warstwy inwersyjnej powierzchni i wskazuje jej wymiary. Warstwa inwersyjna zwęża się, gdy przechodzimy od drenu do źródła. Teraz, jeśli weźmiemy pod uwagę mały obszar dy długości kanału L, wówczas przyrostowy opór dR oferowany przez ten region można wyrazić jako -
$$ dR = - \ frac {dy} {w. \ mu _ {n} .Q1 (y)} $$
Tutaj minus wynika z ujemnej polaryzacji Q1 ładowania warstwa inwersji i μ n jest mobilność powierzchnię, która jest stała. Teraz podstawmy wartość Q1 (y) w równaniu dR -
$$ dR = - \ frac {dy} {w. \ mu _ {n}. \ left \ {-C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right ] -V_ {TO} \ right \}} $$
$$ dR = \ frac {dy} {w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C \ left (Y \ right)} \ right] -V_ {TO} } $$
Teraz spadek napięcia w małym obszarze dy można podać wzorem
$$ dV_ {c} = I_ {D} .dR $$
Umieść wartość dR w powyższym równaniu
$$ dV_ {C} = I_ {D}. \ frac {dy} {w. \ mu_ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} \ right] -V_ {TO}} $$
$$ w. \ mu _ {n} .C_ {ox} \ left [V_ {GS} -V_ {C (Y)} - V_ {TO} \ right] .dV_ {C} = I_ {D} .dy $$
Aby uzyskać ID prądu drenu w całym obszarze kanału, powyższe równanie można scałkować wzdłuż kanału od y = 0 do y = L i napięć V C (y) = 0 do V C (y) = V DS ,
$$ C_ {ox} .w. \ Mu _ {n}. \ Int_ {V_ {c} = 0} ^ {V_ {DS}} \ left [V_ {GS} -V_ {C \ left (Y \ right )} - V_ {TO} \ right] .dV_ {C} = \ int_ {Y = 0} ^ {L} I_ {D} .dy $$
$$ \ frac {C_ {ox} .w. \ mu _ {n}} {2} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) = I_ {D} \ left [L-0 \ right] $$
$$ I_ {D} = \ frac {C_ {ox}. \ Mu _ {n}} {2}. \ Frac {w} {L} \ left (2 \ left [V_ {GS} -V_ {TO} \ right] V_ {DS} -V_ {DS} ^ {2} \ right) $$
Dla regionu liniowego V DS <V GS - V TO . Dla obszaru nasycenia wartość V DS jest większa niż (V GS - V TO ). Dlatego dla regionu nasycenia V DS = (V GS - V TO ).
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [2V_ {DS} \ right] V_ {DS} -V_ { DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {2V_ {DS} ^ {2} -V_ {DS} ^ {2} } {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {V_ {DS} ^ {2}} {L} \ right) $$
$$ I_ {D} = C_ {ox}. \ Mu _ {n}. \ Frac {w} {2} \ left (\ frac {\ left [V_ {GS} -V_ {TO} \ right] ^ { 2}} {L} \ right) $$