Teoria de grafos - Conectividade
Se é possível atravessar um gráfico de um vértice para outro é determinado por como um gráfico é conectado. Conectividade é um conceito básico da Teoria dos Grafos. Conectividade define se um gráfico está conectado ou desconectado. Possui subtópicos baseados em aresta e vértice, conhecidos como conectividade de aresta e conectividade de vértice. Vamos discuti-los em detalhes.
Conectividade
Diz-se que um gráfico é connected if there is a path between every pair of vertex. De cada vértice a qualquer outro vértice, deve haver algum caminho a ser percorrido. Isso é chamado de conectividade de um gráfico. Um gráfico com vários vértices e arestas desconectados é considerado desconectado.
Example 1
No gráfico a seguir, é possível viajar de um vértice para qualquer outro vértice. Por exemplo, pode-se atravessar do vértice 'a' ao vértice 'e' usando o caminho 'ab-e'.
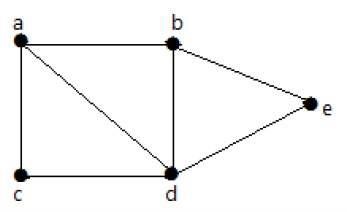
Example 2
No exemplo a seguir, atravessar do vértice 'a' para o vértice 'f' não é possível porque não há nenhum caminho entre eles direta ou indiretamente. Portanto, é um gráfico desconectado.
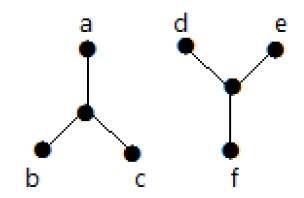
Cut Vertex
Seja 'G' um gráfico conectado. Um vértice V ∈ G é chamado de vértice de corte de 'G', se 'G-V' (Excluir 'V' de 'G') resulta em um gráfico desconectado. Remover um vértice de corte de um gráfico divide-o em dois ou mais gráficos.
Note - Remover um vértice cortado pode tornar um gráfico desconectado.
Um gráfico conectado 'G' pode ter no máximo (n – 2) vértices de corte.
Example
No gráfico a seguir, os vértices 'e' e 'c' são os vértices cortados.

Ao remover 'e' ou 'c', o gráfico se tornará um gráfico desconectado.

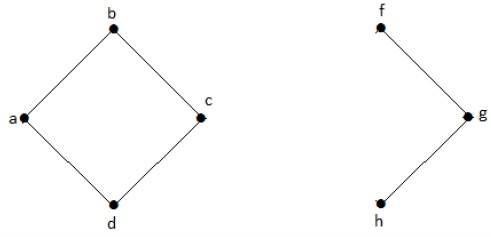
Sem 'g', não há caminho entre o vértice 'c' e o vértice 'h' e muitos outros. Portanto, é um gráfico desconectado com vértice de corte como 'e'. Da mesma forma, 'c' também é um vértice de corte para o gráfico acima.
Borda cortada (ponte)
Seja 'G' um gráfico conectado. Uma aresta 'e' ∈ G é chamada de aresta de corte se 'G-e' resultar em um gráfico desconectado.
Se a remoção de uma borda em um gráfico resultar em dois ou mais gráficos, essa borda é chamada de Corte de Borda.
Example
No gráfico a seguir, a borda de corte é [(c, e)].

Ao remover a aresta (c, e) do gráfico, ele se torna um gráfico desconectado.


No gráfico acima, remover a aresta (c, e) divide o gráfico em dois, que nada mais é do que um gráfico desconectado. Portanto, a aresta (c, e) é uma aresta de corte do gráfico.
Note - Seja 'G' um gráfico conectado com 'n' vértices, então
uma aresta de corte e ∈ G se e somente se a aresta 'e' não fizer parte de qualquer ciclo em G.
o número máximo de arestas de corte possível é 'n-1'.
sempre que houver arestas de corte, vértices de corte também existem porque pelo menos um vértice de uma aresta de corte é um vértice de corte.
se existe um vértice de corte, então uma aresta de corte pode ou não existir.
Corte o conjunto de um gráfico
Seja 'G' = (V, E) um gráfico conectado. Um subconjunto E 'de E é chamado de conjunto de corte de G se a exclusão de todas as arestas de E' de G faz G desconectar.
Se a exclusão de um certo número de arestas de um gráfico o desconecta, então essas arestas excluídas são chamadas de conjunto de corte do gráfico.
Example
Dê uma olhada no gráfico a seguir. Seu conjunto de corte é E1 = {e1, e3, e5, e8}.
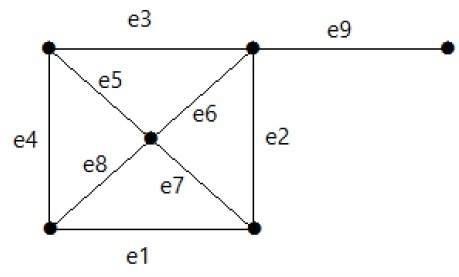
Depois de remover o conjunto de corte E1 do gráfico, ele aparecerá da seguinte forma -
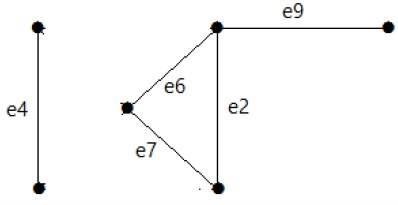
Da mesma forma, existem outros conjuntos de corte que podem desconectar o gráfico -
E3 = {e9} - Menor conjunto de corte do gráfico.
E4 = {e3, e4, e5}
Edge Connectivity
Seja 'G' um gráfico conectado. O número mínimo de arestas cuja remoção torna 'G' desconectado é chamado de conectividade de aresta de G.
Notation - λ (G)
Em outras palavras, o number of edges in a smallest cut set of G é chamada de conectividade de borda de G.
Se 'G' tem uma borda de corte, então λ (G) é 1. (conectividade de borda de G.)
Example
Dê uma olhada no gráfico a seguir. Ao remover duas arestas mínimas, o gráfico conectado se desconecta. Portanto, sua conectividade de borda (λ (G)) é 2.
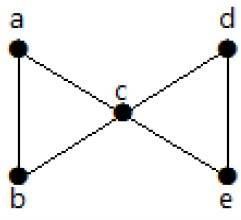
Aqui estão as quatro maneiras de desconectar o gráfico removendo duas arestas -

Vertex Connectivity
Seja 'G' um gráfico conectado. O número mínimo de vértices cuja remoção torna 'G' desconectado ou reduz 'G' a um grafo trivial é chamado de conectividade de vértice.
Notation - K (G)
Example
No gráfico acima, remover os vértices 'e' e 'i' faz com que o gráfico se desconecte.

Se G tem um vértice de corte, então K (G) = 1.
Notation - Para qualquer gráfico conectado G,
K (G) ≤ λ (G) ≤ δ (G)
Conectividade de vértices (K (G)), conectividade de borda (λ (G)), número mínimo de graus de G (δ (G)).
Example
Calcule λ (G) e K (G) para o gráfico a seguir -
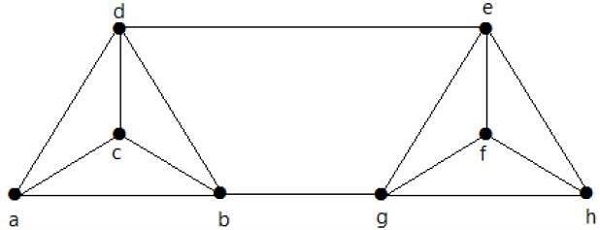
Solution
No gráfico,
δ (G) = 3
K (G) ≤ λ (G) ≤ δ (G) = 3 (1)
K (G) ≥ 2 (2)
Excluindo as arestas {d, e} e {b, h}, podemos desconectar G.
Portanto,
λ (G) = 2
2 ≤ λ (G) ≤ δ (G) = 2 (3)
De (2) e (3), conectividade de vértice K (G) = 2