Teoria de grafos - Matchings
Um gráfico correspondente é um subgráfico de um gráfico onde não há arestas adjacentes umas às outras. Simplesmente, não deve haver nenhum vértice comum entre duas arestas.
Coincidindo
Seja 'G' = (V, E) um gráfico. Um subgrafo é chamado de M (G) correspondente,if each vertex of G is incident with at most one edge in M, ou seja,
deg (V) ≤ 1 ∀ V ∈ G
o que significa que no grafo de casamento M (G), os vértices devem ter grau 1 ou 0, onde as arestas devem incidir no grafo G.
Notation - M (G)
Example
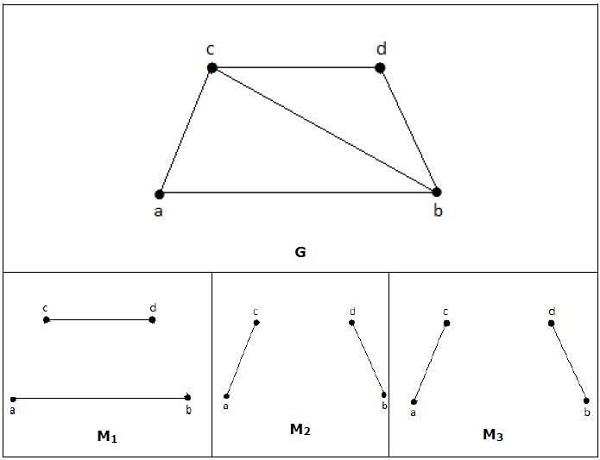

Em uma correspondência,
se deg (V) = 1, então (V) é considerado compatível
se deg (V) = 0, então (V) não é correspondido.
Em uma correspondência, não há duas arestas adjacentes. É porque se quaisquer duas arestas forem adjacentes, então o grau do vértice que está unindo essas duas arestas terá um grau 2, o que viola a regra de correspondência.
Correspondência máxima
Um M correspondente do gráfico 'G' é dito máximo if no other edges of ‘G’ can be added to M.
Example

M1, M2, M3 do gráfico acima são a correspondência máxima de G.
Combinação Máxima
Também é conhecido como maior correspondência máxima. A correspondência máxima é definida como a correspondência máxima com o número máximo de arestas.
O número de arestas na combinação máxima de 'G' é chamado de matching number.
Example
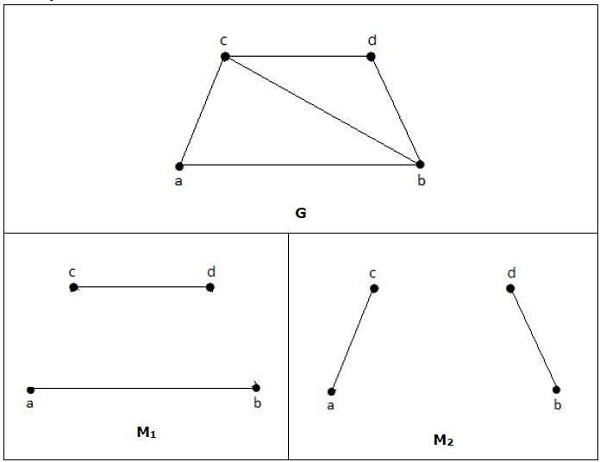
Para um gráfico dado no exemplo acima, M1 e M2 são a correspondência máxima de 'G' e seu número correspondente é 2. Portanto, usando o gráfico G, podemos formar apenas os subgráficos com apenas 2 arestas no máximo. Portanto, temos o número correspondente como dois.
Combinação Perfeita
Uma correspondência (M) do gráfico (G) é considerada uma correspondência perfeita, se cada vértice do gráfico g (G) incide exatamente em uma aresta da correspondência (M), ou seja,
deg (V) = 1 ∀ V
O grau de cada vértice no subgrafo deve ter um grau de 1.
Example
Nos gráficos a seguir, M1 e M2 são exemplos de combinação perfeita de G.
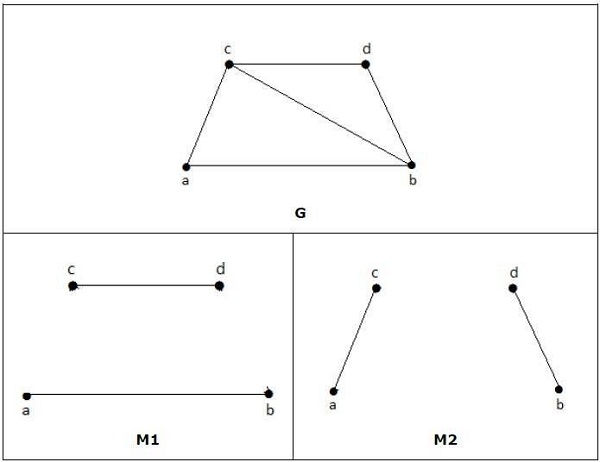
Note - Cada combinação perfeita de gráfico também é uma combinação máxima de gráfico, porque não há chance de adicionar mais uma aresta em um gráfico de combinação perfeita.
Uma correspondência máxima do gráfico não precisa ser perfeita. Se um gráfico 'G' tem uma correspondência perfeita, então o número de vértices | V (G) | é mesmo. Se for ímpar, então o último vértice emparelha-se com o outro vértice e, finalmente, permanece um único vértice que não pode ser emparelhado com nenhum outro vértice cujo grau seja zero. Isso viola claramente o princípio da combinação perfeita.
Example
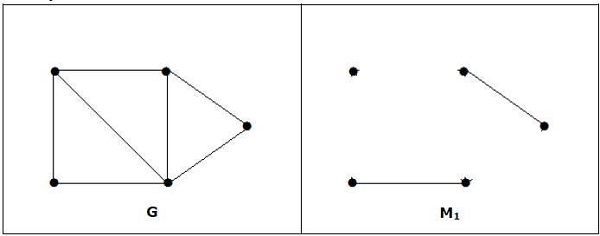
Note- O inverso da afirmação acima não precisa ser verdadeiro. Se G tiver um número par de vértices, M1 não precisa ser perfeito.
Example
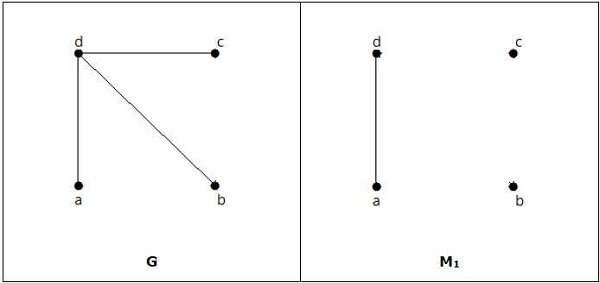
Está combinando, mas não é uma combinação perfeita, embora tenha um número par de vértices.