Teoria dos Grafos - Fundamentos

Um gráfico é um diagrama de pontos e linhas conectadas aos pontos. Ele tem pelo menos uma linha unindo um conjunto de dois vértices sem nenhum vértice se conectando. O conceito de grafos na teoria dos grafos se sustenta em alguns termos básicos como ponto, linha, vértice, aresta, grau de vértices, propriedades dos grafos, etc. Aqui, neste capítulo, cobriremos esses fundamentos da teoria dos grafos.

Ponto

A pointé uma posição particular em um espaço unidimensional, bidimensional ou tridimensional. Para melhor compreensão, um ponto pode ser denotado por um alfabeto. Ele pode ser representado com um ponto.

Exemplo

Aqui, o ponto é um ponto denominado 'a'.

Linha

UMA Lineé uma conexão entre dois pontos. Ele pode ser representado com uma linha sólida.

Example

Aqui, 'a' e 'b' são os pontos. A ligação entre esses dois pontos é chamada de linha.

Vértice

Um vértice é um ponto onde várias linhas se encontram. Também é chamado denode. Semelhante aos pontos, um vértice também é denotado por um alfabeto.

Example

Aqui, o vértice é nomeado com um alfabeto 'a'.

Beira

Uma aresta é o termo matemático para uma linha que conecta dois vértices. Muitas arestas podem ser formadas a partir de um único vértice. Sem um vértice, uma aresta não pode ser formada. Deve haver um vértice inicial e um vértice final para uma aresta.

Example

Aqui, 'a' e 'b' são os dois vértices e a ligação entre eles é chamada de aresta.

Gráfico

Um gráfico 'G' é definido como G = (V, E) Onde V é um conjunto de todos os vértices e E é um conjunto de todas as arestas do gráfico.

Example 1

No exemplo acima, ab, ac, cd e bd são as arestas do gráfico. Da mesma forma, a, b, c e d são os vértices do gráfico.

Example 2

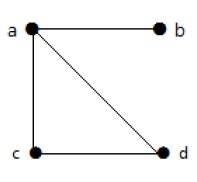
Neste gráfico, existem quatro vértices a, b, c e d e quatro arestas ab, ac, ad e cd.

Ciclo

Em um gráfico, se uma aresta é desenhada do vértice até ela mesma, é chamada de loop.

Example 1

No gráfico acima, V é um vértice para o qual possui uma aresta (V, V) formando um loop.

Example 2

Neste gráfico, há dois loops que são formados no vértice a e no vértice b.

Grau de Vértice

É o número de vértices adjacentes a um vértice V.

Notation - deg (V).

Em um gráfico simples com n número de vértices, o grau de qualquer vértice é -

deg (v) ≤ n - 1 ∀ v ∈ G

Um vértice pode formar uma aresta com todos os outros vértices, exceto por ele mesmo. Portanto, o grau de um vértice será até onumber of vertices in the graph minus 1. Este 1 é para o autovértex, pois ele não pode formar um loop por si mesmo. Se houver um loop em qualquer um dos vértices, então não é um gráfico simples.

O grau de vértice pode ser considerado em dois casos de gráficos -

• Gráfico não direcionado

• Gráfico Direcionado

Grau de vértice em um gráfico não direcionado

Um gráfico não direcionado não possui arestas direcionadas. Considere os seguintes exemplos.

Example 1

Dê uma olhada no gráfico a seguir -

No gráfico não direcionado acima,

• deg (a) = 2, pois há 2 arestas que se encontram no vértice 'a'.

• deg (b) = 3, pois há 3 arestas que se encontram no vértice 'b'.

• deg (c) = 1, pois há 1 aresta formada no vértice 'c'

• Então, 'c' é um pendent vertex.

• deg (d) = 2, pois há 2 arestas que se encontram no vértice 'd'.

• deg (e) = 0, pois há 0 arestas formadas no vértice 'e'.

• Então, 'e' é um isolated vertex.

Example 2

Dê uma olhada no gráfico a seguir -

No gráfico acima,

deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 e deg (e) = 0.

O vértice 'e' é um vértice isolado. O gráfico não possui vértices pendentes.

Grau de vértice em um gráfico direcionado

Em um gráfico direcionado, cada vértice tem um indegree e um outdegree.

Indegree de um gráfico

• Indegree do vértice V é o número de arestas que estão entrando no vértice V.

• Notation - deg− (V).

Outdegree of a Graph

• Outdegree do vértice V é o número de arestas que estão saindo do vértice V.

• Notation - deg + (V).

Considere os seguintes exemplos.

Example 1

Dê uma olhada no seguinte gráfico direcionado. O vértice 'a' tem duas arestas, 'ad' e 'ab', que vão para fora. Conseqüentemente, seu grau externo é 2. Similarmente, há uma aresta 'ga', vindo em direção ao vértice 'a'. Portanto, o indegree de 'a' é 1.

O indegree e outdegree de outros vértices são mostrados na tabela a seguir -

Vértice	Indegree	Outdegree
uma	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

Example 2

Dê uma olhada no seguinte gráfico direcionado. O vértice 'a' tem uma aresta 'ae' saindo do vértice 'a'. Portanto, seu grau de diferença é 1. Da mesma forma, o gráfico tem uma aresta 'ba' indo em direção ao vértice 'a'. Portanto, o indegree de 'a' é 1.

O indegree e outdegree de outros vértices são mostrados na tabela a seguir -

Vértice	Indegree	Outdegree
uma	1	1
b	0	2
c	2	0
d	1	1
e	1	1

Vértice Pendente

Ao usar o grau de um vértice, temos dois tipos especiais de vértices. Um vértice com grau um é chamado de vértice pendente.

Example

Aqui, neste exemplo, o vértice 'a' e o vértice 'b' têm uma aresta conectada 'ab'. Portanto, com relação ao vértice 'a', há apenas uma aresta em direção ao vértice 'b' e, da mesma forma, em relação ao vértice 'b', há apenas uma aresta em direção ao vértice 'a'. Finalmente, o vértice 'a' e o vértice 'b' têm grau como um, que também são chamados de vértices pendentes.

Vértice Isolado

Um vértice com grau zero é chamado de vértice isolado.

Example

Aqui, o vértice 'a' e o vértice 'b' não têm conectividade entre si e também com quaisquer outros vértices. Portanto, o grau de ambos os vértices 'a' e 'b' são zero. Eles também são chamados de vértices isolados.

Adjacência

Aqui estão as normas de adjacência -

• Em um gráfico, dois vértices são considerados adjacent, se houver uma aresta entre os dois vértices. Aqui, a adjacência dos vértices é mantida pela única aresta que está conectando esses dois vértices.

• Em um gráfico, duas arestas são ditas adjacentes, se houver um vértice comum entre as duas arestas. Aqui, a adjacência das arestas é mantida pelo único vértice que conecta duas arestas.

Example 1

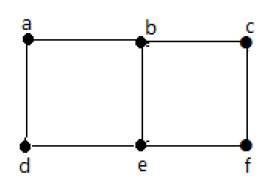
No gráfico acima -

• 'a' e 'b' são os vértices adjacentes, pois existe uma aresta comum 'ab' entre eles.

• 'a' e 'd' são os vértices adjacentes, pois existe uma aresta comum 'ad' entre eles.

• ab 'e' be 'são as arestas adjacentes, pois existe um vértice comum' b 'entre elas.

• be 'e' de 'são as arestas adjacentes, pois existe um vértice comum' e 'entre elas.

Example 2

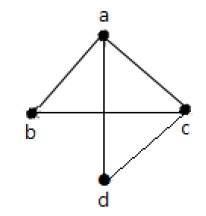
No gráfico acima -

• 'a' e 'd' são os vértices adjacentes, pois existe uma aresta comum 'ad' entre eles.

• 'c' e 'b' são os vértices adjacentes, pois existe uma aresta comum 'cb' entre eles.

• 'ad' e 'cd' são as arestas adjacentes, pois existe um vértice comum 'd' entre elas.

• 'ac' e 'cd' são as arestas adjacentes, pois existe um vértice comum 'c' entre elas.

Bordas Paralelas

Em um gráfico, se um par de vértices é conectado por mais de uma aresta, essas arestas são chamadas de arestas paralelas.

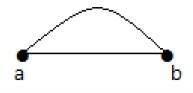
No gráfico acima, 'a' e 'b' são os dois vértices que são conectados por duas arestas 'ab' e 'ab' entre eles. Por isso é chamado de aresta paralela.

Multi Graph

Um gráfico com arestas paralelas é conhecido como Multigraph.

Example 1

No gráfico acima, existem cinco arestas 'ab', 'ac', 'cd', 'cd' e 'bd'. Uma vez que 'c' e 'd' têm duas arestas paralelas entre eles, é um multigrafo.

Example 2

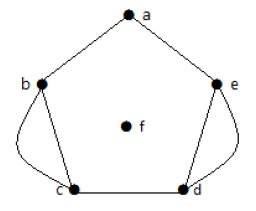
No gráfico acima, os vértices 'b' e 'c' possuem duas arestas. Os vértices 'e' e 'd' também possuem duas arestas entre eles. Portanto, é um Multigraph.

Sequência de Graus de um Gráfico

Se os graus de todos os vértices de um gráfico forem organizados em ordem decrescente ou crescente, a sequência obtida é conhecida como sequência de graus do gráfico.

Example 1

Vértice	UMA	b	c	d	e
Conectando à	b, c	de Anúncios	de Anúncios	c, b, e	d
Grau	2	2	2	3	1

No gráfico acima, para os vértices {d, a, b, c, e}, a sequência de graus é {3, 2, 2, 2, 1}.

Example 2

Vértice	UMA	b	c	d	e	f
Conectando à	estar	a, c	b, d	c, e	de Anúncios	-
Grau	2	2	2	2	2	0

No gráfico acima, para os vértices {a, b, c, d, e, f}, a sequência de graus é {2, 2, 2, 2, 2, 0}.