Teoria de grafos - transversabilidade
Um gráfico é percorrível se você puder desenhar um caminho entre todos os vértices sem refazer o mesmo caminho. Com base nesse caminho, existem algumas categorias, como o caminho de Euler e o circuito de Euler, que são descritos neste capítulo.
Caminho de Euler
O caminho de Euler contém cada aresta de 'G' exatamente uma vez e cada vértice de 'G' pelo menos uma vez. Um grafo conectado G é considerado percorrível se contiver um caminho de Euler.
Example
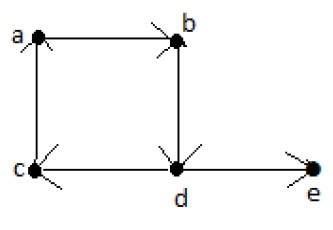
Caminho de Euler = dcabde.
Circuito de Euler
No caminho de Euler, se o vértice inicial é igual ao vértice final, ele é chamado de circuito de Euler.
Example
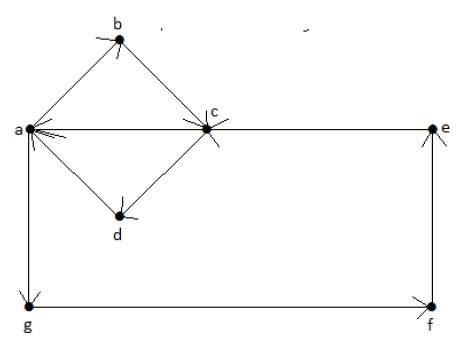
Euler’s Path = abcdagfeca.
Teorema do Circuito de Euler
Um grafo conectado 'G' é percorrível se e somente se o número de vértices com grau ímpar em G for exatamente 2 ou 0. Um grafo conectado G pode conter um caminho de Euler, mas não um circuito de Euler, se tiver exatamente dois vértices com um grau estranho.
Note - Este caminho de Euler começa com um vértice de grau ímpar e termina com o outro vértice de grau ímpar.
Example
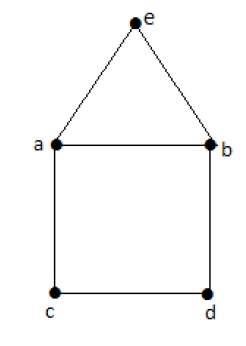
Euler’s Path- beabdca não é um circuito de Euler, mas é um caminho de Euler. É claro que tem exatamente 2 vértices de grau ímpar.
Note - Em um grafo conectado G, se o número de vértices com grau ímpar = 0, então o circuito de Euler existe.
Gráfico Hamiltoniano
Um grafo conectado G é considerado um grafo hamiltoniano, se existir um ciclo que contenha todos os vértices de G.
Cada ciclo é um circuito, mas um circuito pode conter vários ciclos. Esse ciclo é chamado deHamiltonian cycle de G.
Caminho Hamiltoniano
Um gráfico conectado é considerado hamiltoniano se contiver cada vértice de G exatamente uma vez. Esse caminho é chamado deHamiltonian path.
Example
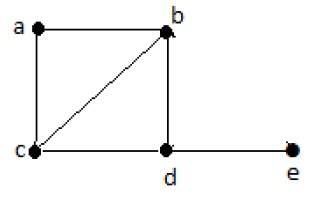
Hamiltonian Path- edbac.
Note
O circuito de Euler contém cada aresta do gráfico exatamente uma vez.
Em um ciclo hamiltoniano, algumas arestas do gráfico podem ser ignoradas.
Example
Dê uma olhada no gráfico a seguir -
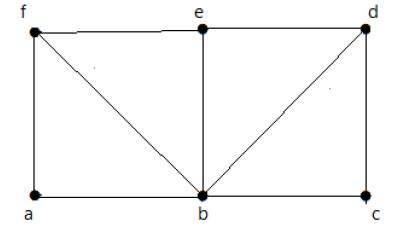
Para o gráfico mostrado acima -
Existe caminho de Euler - falso
Circuito de Euler existe - falso
Existe ciclo hamiltoniano - verdadeiro
Existe caminho hamiltoniano - verdadeiro
G tem quatro vértices com grau ímpar, portanto não é percorrível. Ao pular as arestas internas, o gráfico tem um ciclo hamiltoniano passando por todos os vértices.