Teoria de grafos - Conjuntos independentes

Conjuntos independentes são representados em conjuntos, nos quais

• não deveria haver any edges adjacent to each other. Não deve haver nenhum vértice comum entre duas arestas.

• não deveria haver any vertices adjacent to each other. Não deve haver nenhuma aresta comum entre dois vértices.

Conjunto de linha independente

Seja 'G' = (V, E) um gráfico. Um subconjunto L de E é chamado de conjunto de linha independente de 'G' se não houver duas arestas em L adjacentes. Esse conjunto é chamado de conjunto de linha independente.

Example

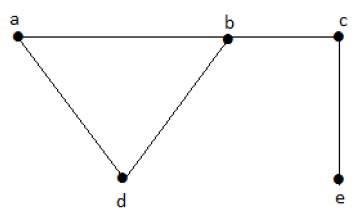
Vamos considerar os seguintes subconjuntos -

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

Neste exemplo, os subconjuntos L2 e L3 não são claramente as arestas adjacentes no gráfico fornecido. Eles são conjuntos de linhas independentes. No entanto, L1 não é um conjunto de linhas independentes, pois para fazer um conjunto de linhas independentes, deve haver pelo menos duas arestas.

Conjunto de linha independente máxima

Um conjunto de linhas independentes é considerado o conjunto máximo de linhas independentes de um gráfico 'G' se nenhuma outra aresta de 'G' puder ser adicionada a 'L'.

Example

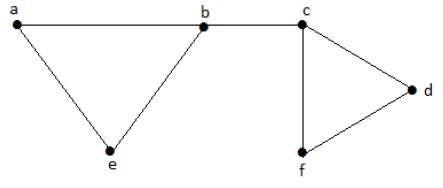
Vamos considerar os seguintes subconjuntos -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ e L ₃ são conjuntos de linhas independentes máximas / correspondência máxima. Quanto a apenas esses dois subconjuntos, não há chance de adicionar qualquer outra aresta que não seja adjacente. Portanto, esses dois subconjuntos são considerados os conjuntos de linhas independentes máximas.

Conjunto de linha independente máximo

Um conjunto máximo de linhas independentes de 'G' com o número máximo de arestas é chamado de conjunto máximo de linhas independentes 'G'.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

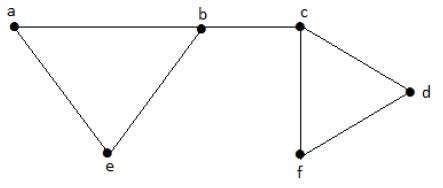
Vamos considerar os seguintes subconjuntos -

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ é o conjunto máximo de linhas independentes de G com arestas máximas que não são as arestas adjacentes no gráfico e é denotado por β1 = 3.

Note - Para qualquer gráfico G sem vértice isolado,

α1 + β1 = número de vértices em um gráfico = | V |

Example

Número de cobertura de linha de K _n / C _n / w _n ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {casos} \ frac {n} {2} \: se \: n \: é \: par \\\ frac {n + 1} {2} \: if \: n \: é \: ímpar \ final {casos} $$

Número independente de linha (número correspondente) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Conjunto de vértices independentes

Seja 'G' = (V, E) um gráfico. Um subconjunto de 'V' é chamado de conjunto independente de 'G' se não houver dois vértices em 'S' adjacentes.

Example

Considere os seguintes subconjuntos dos gráficos acima -

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Claramente S ₁ não é um conjunto de vértices independente, porque para obter um conjunto de vértices independente, deve haver pelo menos dois vértices em um gráfico. Mas aqui não é esse o caso. Os subconjuntos S ₂ , S ₃ e S ₄ são os conjuntos de vértices independentes porque não há nenhum vértice adjacente a qualquer vértice dos subconjuntos.

Conjunto de vértices independentes máximos

Seja 'G' um gráfico, então um conjunto independente de vértices de 'G' é considerado máximo se nenhum outro vértice de 'G' puder ser adicionado a 'S'.

Example

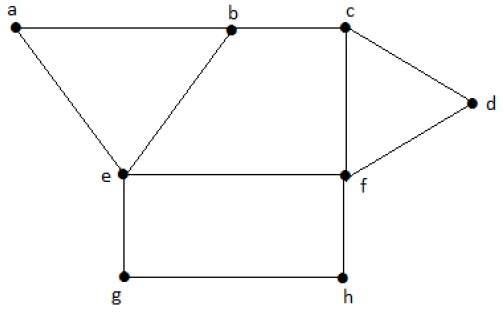
Considere os seguintes subconjuntos dos gráficos acima.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ e S ₃ são conjuntos de vértices independentes máximos de 'G'. Em S ₁ e S ₄ , podemos adicionar outros vértices; mas em S ₂ e S ₃ , não podemos adicionar nenhum outro vértice.

Conjunto de vértices independentes máximo

Um conjunto máximo de vértices independente de 'G' com o número máximo de vértices é chamado de conjunto máximo de vértices independentes.

Example

Considere os seguintes subconjuntos do gráfico acima -

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Apenas S ₃ é o conjunto máximo de vértices independentes, pois cobre o maior número de vértices. O número de vértices em um conjunto máximo de vértices independentes de 'G' é chamado de número de vértices independentes de G (β ₂ ).

Example

Para o gráfico completo K _n ,

Número de cobertura do vértice = α ₂ = n − 1

Número independente do vértice = β ₂ = 1

Você tem α ₂ + β ₂ = n

Em um gráfico completo, cada vértice é adjacente aos seus (n - 1) vértices restantes. Portanto, um conjunto máximo independente de K _n contém apenas um vértice.

Portanto, β ₂ = 1

e α ₂ = | v | - β ₂ = n-1

Note - Para qualquer gráfico 'G' = (V, E)

• α ₂ + β ₂ = | v |
• Se 'S' é um conjunto de vértices independente de 'G', então (V - S) é uma cobertura de vértices de G.