Teoria de grafos - coberturas

Um gráfico de cobertura é um subgrafo que contém todos os vértices ou todas as arestas correspondentes a algum outro gráfico. Um subgrafo que contém todos os vértices é chamado deline/edge covering. Um subgrafo que contém todas as arestas é chamado devertex covering.

Cobertura de Linha

Seja G = (V, E) um gráfico. Um subconjunto C (E) é chamado de cobertura de linha de G se cada vértice de G incide com pelo menos uma aresta em C, ou seja,

deg (V) ≥ 1 ∀ V ∈ G

porque cada vértice está conectado a outro vértice por uma aresta. Portanto, tem um grau mínimo de 1.

Example

Dê uma olhada no gráfico a seguir -

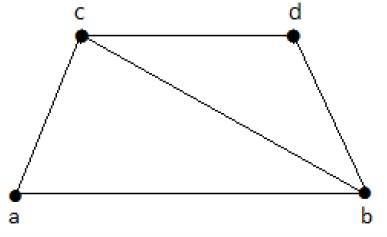
Seus subgráficos com cobertura de linha são os seguintes -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

A linha de cobertura de 'G' não existe se e somente se 'G' tem um vértice isolado. A cobertura da linha de um gráfico com 'n' vértices tem pelo menos [n / 2] arestas.

Cobertura mínima de linha

Uma linha cobrindo C de um gráfico G é considerada mínima if no edge can be deleted from C.

Example

No gráfico acima, os subgráficos com cobertura de linha são os seguintes -

C ₁ = {{a, b}, {c, d}}

C ₂ = {{a, d}, {b, c}}

C ₃ = {{a, b}, {b, c}, {b, d}}

C ₄ = {{a, b}, {b, c}, {c, d}}

Aqui, C ₁ , C ₂ , C ₃ são coberturas de linha mínimas, enquanto C ₄ não é, porque podemos excluir {b, c}.

Cobertura mínima de linha

Também é conhecido como Smallest Minimal Line Covering. Uma cobertura de linha mínima com número mínimo de bordas é chamada de cobertura de linha mínima de 'G'. O número de arestas em uma linha mínima cobrindo em 'G' é chamado deline covering numberde 'G' (α ₁ ).

Example

No exemplo acima, C ₁ e C ₂ são a cobertura de linha mínima de G e α ₁ = 2.

Cada cobertura de linha contém uma cobertura de linha mínima.
Cada cobertura de linha não contém uma cobertura de linha mínima (C ₃ não contém nenhuma cobertura de linha mínima.
Nenhuma cobertura de linha mínima contém um ciclo.
Se uma linha cobrindo 'C' não contém caminhos de comprimento 3 ou mais, então 'C' é uma linha mínima cobrindo porque todos os componentes de 'C' são gráfico de estrela e de um gráfico de estrela, nenhuma aresta pode ser excluída.

Cobertura de vértices

Seja 'G' = (V, E) um gráfico. Um subconjunto K de V é chamado de cobertura de vértice de 'G', se toda aresta de 'G' incide ou é coberta por um vértice em 'K'.

Example

Dê uma olhada no gráfico a seguir -

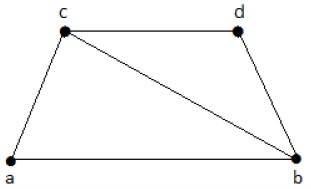
Os subgráficos que podem ser derivados do gráfico acima são os seguintes -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

K ₄ = {a, d}

Aqui, K ₁ , K ₂ e K ₃ têm cobertura de vértices, enquanto K ₄ não tem cobertura de vértices, pois não cobre a aresta {bc}.

Cobertura mínima de vértices

Um vértice 'K' do gráfico 'G' é considerado um vértice mínimo cobrindo se nenhum vértice puder ser excluído de 'K'.

Example

No gráfico acima, os subgráficos com cobertura de vértices são os seguintes -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}

Aqui, K ₁ e K ₂ são coberturas de vértices mínimas, enquanto em K ₃ , o vértice 'd' pode ser excluído.

Cobertura mínima do vértice

É também conhecido como a menor cobertura mínima do vértice. Uma cobertura mínima de vértices do gráfico 'G' com um número mínimo de vértices é chamada de cobertura mínima de vértices.

O número de vértices em um vértice mínimo cobrindo 'G' é chamado de vértice cobrindo o número de G (α ₂ ).

Example

No gráfico a seguir, os subgráficos com cobertura de vértices são os seguintes -

K ₁ = {b, c}

K ₂ = {a, b, c}

K ₃ = {b, c, d}