Аналитика больших данных - статистические методы

При анализе данных можно использовать статистический подход. Основные инструменты, необходимые для выполнения базового анализа:

• Корреляционный анализ
• Анализ отклонений
• Проверка гипотезы

При работе с большими наборами данных это не представляет проблемы, поскольку эти методы не требуют больших вычислительных ресурсов, за исключением корреляционного анализа. В этом случае всегда можно взять образец, и результаты должны быть надежными.

Корреляционный анализ

Корреляционный анализ стремится найти линейные отношения между числовыми переменными. Это может быть полезно в разных обстоятельствах. Одним из распространенных способов использования является исследовательский анализ данных; в разделе 16.0.2 книги есть базовый пример этого подхода. Прежде всего, метрика корреляции, используемая в упомянутом примере, основана наPearson coefficient. Однако есть еще одна интересная метрика корреляции, на которую не влияют выбросы. Этот показатель называется корреляцией Спирмена.

В spearman correlation метрика более устойчива к наличию выбросов, чем метод Пирсона, и дает лучшие оценки линейных отношений между числовыми переменными, когда данные не распределены нормально.

library(ggplot2)

# Select variables that are interesting to compare pearson and spearman 
correlation methods. 
x = diamonds[, c('x', 'y', 'z', 'price')]  

# From the histograms we can expect differences in the correlations of both 
metrics.  
# In this case as the variables are clearly not normally distributed, the 
spearman correlation 

# is a better estimate of the linear relation among numeric variables. 
par(mfrow = c(2,2)) 
colnm = names(x) 
for(i in 1:4) { 
   hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i])) 
} 
par(mfrow = c(1,1))

Из гистограмм на следующем рисунке мы можем ожидать различий в корреляциях обоих показателей. В этом случае, поскольку переменные явно не имеют нормального распределения, корреляция Спирмена является лучшей оценкой линейной связи между числовыми переменными.

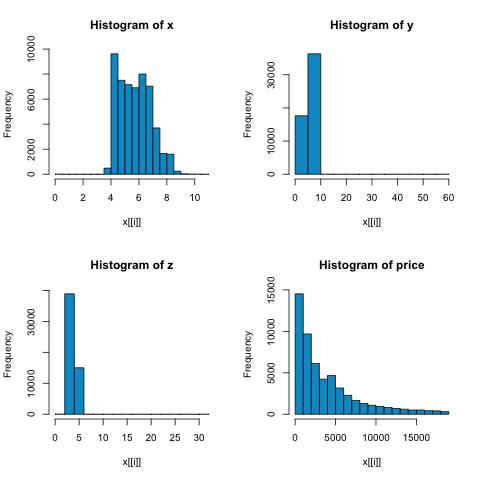
Чтобы вычислить корреляцию в R, откройте файл bda/part2/statistical_methods/correlation/correlation.R который имеет этот раздел кода.

## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson') 
cor_spearman <- cor(x, method = 'spearman')  

### Pearson Correlation 
print(cor_pearson) 
#            x          y          z        price 
# x      1.0000000  0.9747015  0.9707718  0.8844352 
# y      0.9747015  1.0000000  0.9520057  0.8654209 
# z      0.9707718  0.9520057  1.0000000  0.8612494 
# price  0.8844352  0.8654209  0.8612494  1.0000000  

### Spearman Correlation 
print(cor_spearman) 
#              x          y          z      price 
# x      1.0000000  0.9978949  0.9873553  0.9631961 
# y      0.9978949  1.0000000  0.9870675  0.9627188 
# z      0.9873553  0.9870675  1.0000000  0.9572323 
# price  0.9631961  0.9627188  0.9572323  1.0000000

Тест хи-квадрат

Тест хи-квадрат позволяет нам проверить, независимы ли две случайные величины. Это означает, что распределение вероятностей каждой переменной не влияет на другую. Чтобы оценить тест в R, нам нужно сначала создать таблицу непредвиденных обстоятельств, а затем передать ее вchisq.test R функция.

Например, давайте проверим, существует ли связь между переменными: огранка и цвет из набора данных бриллиантов. Тест формально определяется как -

• H0: переменная огранка и алмаз независимы
• H1: переменная огранка и алмаз не являются независимыми

Мы могли бы предположить, что между этими двумя переменными существует связь по их имени, но тест может дать объективное «правило», говорящее, насколько значим этот результат или нет.

В следующем фрагменте кода мы обнаружили, что значение p теста составляет 2,2e-16, что практически равно нулю. Затем после запуска теста выполнитеMonte Carlo simulation, мы обнаружили, что значение p равно 0,0004998, что все еще значительно ниже порогового значения 0,05. Этот результат означает, что мы отвергаем нулевую гипотезу (H0), поэтому считаем, что переменныеcut а также color не независимы.

library(ggplot2)

# Use the table function to compute the contingency table 
tbl = table(diamonds$cut, diamonds$color) 
tbl  

#              D    E    F    G    H    I    J 
# Fair       163  224  312  314  303  175  119 
# Good       662  933  909  871  702  522  307 
# Very Good 1513 2400 2164 2299 1824 1204  678 
# Premium   1603 2337 2331 2924 2360 1428  808 
# Ideal     2834 3903 3826 4884 3115 2093  896  

# In order to run the test we just use the chisq.test function. 
chisq.test(tbl)  

# Pearson’s Chi-squared test 
# data:  tbl 
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation 
# It's needed to add the simulate.p.value = TRUE flag and the amount of 
simulations 
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)  

# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) 
# data:  tbl 
# X-squared = 310.32, df = NA, p-value = 0.0004998

Т-тест

Идея t-testсостоит в том, чтобы оценить, есть ли различия в распределении числовой переменной # между разными группами номинальной переменной. Чтобы продемонстрировать это, я выберу уровни Справедливого и Идеального уровней сокращения факторной переменной, а затем мы сравним значения числовой переменной среди этих двух групп.

data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]

data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the 
cut variable 
df1 = data[, c('cut', 'price')]  

# We can see the price means are different for each group 
tapply(df1$price, df1$cut, mean) 
# Fair    Ideal  
# 4358.758 3457.542

T-тесты реализованы в R с t.testфункция. Интерфейс формулы для t.test - самый простой способ его использования, идея состоит в том, что числовая переменная объясняется групповой переменной.

Например: t.test(numeric_variable ~ group_variable, data = data). В предыдущем примереnumeric_variable является price и group_variable является cut.

Со статистической точки зрения мы проверяем, есть ли различия в распределении числовой переменной между двумя группами. Формально проверка гипотезы описывается нулевой (H0) гипотезой и альтернативной гипотезой (H1).

• H0: Нет различий в распределении переменной цены между группами Fair и Ideal.

• H1 Существуют различия в распределении переменной цены между группами Fair и Ideal.

Следующее может быть реализовано в R с помощью следующего кода -

t.test(price ~ cut, data = data)

# Welch Two Sample t-test 
#  
# data:  price by cut 
# t = 9.7484, df = 1894.8, p-value < 2.2e-16 
# alternative hypothesis: true difference in means is not equal to 0 
# 95 percent confidence interval: 
#   719.9065 1082.5251 
# sample estimates: 
#   mean in group Fair mean in group Ideal  
#   4358.758            3457.542   

# Another way to validate the previous results is to just plot the 
distributions using a box-plot 
plot(price ~ cut, data = data, ylim = c(0,12000),  
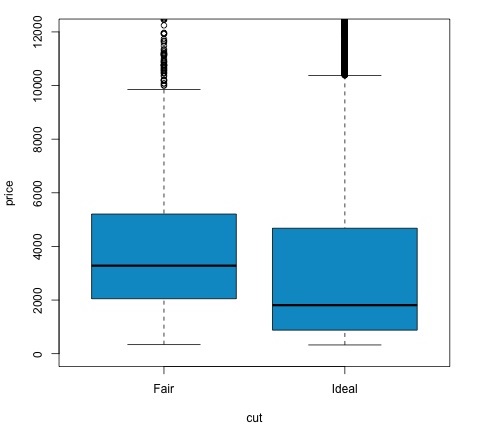
   col = 'deepskyblue3')

Мы можем проанализировать результат теста, проверив, меньше ли p-значение 0,05. Если это так, мы сохраняем альтернативную гипотезу. Это означает, что мы обнаружили разницу в цене между двумя уровнями фактора сокращения. По названиям уровней мы ожидали такого результата, но не ожидали, что средняя цена в группе Fail будет выше, чем в группе Ideal. Мы можем убедиться в этом, сравнив средние значения каждого фактора.

В plotкоманда создает график, показывающий взаимосвязь между ценой и переменной сокращения. Это коробчатый сюжет; мы рассмотрели этот график в разделе 16.0.1, но в основном он показывает распределение переменной цены для двух уровней сокращения, которые мы анализируем.

Анализ отклонений

Дисперсионный анализ (ANOVA) - это статистическая модель, используемая для анализа различий между распределением групп путем сравнения среднего и дисперсии каждой группы, модель была разработана Рональдом Фишером. ANOVA обеспечивает статистический тест того, равны ли средние значения нескольких групп, и поэтому обобщает t-критерий более чем на две группы.

ANOVA полезны для сравнения трех или более групп на предмет статистической значимости, потому что выполнение нескольких двух выборочных t-тестов приведет к увеличению вероятности совершения статистической ошибки типа I.

Что касается математического объяснения, для понимания теста необходимо следующее.

х _IJ = х + (х _я - х) + (х _IJ - х)

Это приводит к следующей модели -

x _ij = μ + α _i + ∈ _ij

где μ - большое среднее, а α _i - i-е групповое среднее. Предполагается, что член ошибки ∈ _ij равен iid из нормального распределения. Нулевая гипотеза теста заключается в том, что -

α ₁ = α ₂ =… = α _k

Что касается вычисления статистики теста, нам нужно вычислить два значения:

• Сумма квадратов разницы между группами -

$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$

• Суммы квадратов внутри групп

$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$

где SSD _B имеет степень свободы k − 1, а SSD _W имеет степень свободы N − k. Затем мы можем определить среднеквадратичные разности для каждой метрики.

MS _B = SSD _B / (k - 1)

MS _w = SSD _w / (N - k)

Наконец, статистика теста в ANOVA определяется как отношение двух вышеуказанных величин.

F = MS _B / MS _w

которое следует F-распределению с k − 1 и N − k степенями свободы. Если нулевая гипотеза верна, F, вероятно, будет близко к 1. В противном случае среднеквадратическое значение MSB между группами, вероятно, будет большим, что приведет к большому значению F.

По сути, ANOVA исследует два источника общей дисперсии и видит, какая часть вносит больший вклад. Вот почему это называется дисперсионным анализом, хотя целью является сравнение групповых средних.

Что касается вычисления статистики, это довольно просто сделать в R. Следующий пример продемонстрирует, как это делается, и построит график результатов.

library(ggplot2)
# We will be using the mtcars dataset 

head(mtcars) 
#                    mpg  cyl disp  hp drat  wt  qsec   vs am  gear carb 
# Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4 
# Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4 
# Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1 
# Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1 
# Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2 
# Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1  

# Let's see if there are differences between the groups of cyl in the mpg variable. 
data = mtcars[, c('mpg', 'cyl')]  
fit = lm(mpg ~ cyl, data = mtcars) 
anova(fit)  

# Analysis of Variance Table 
# Response: mpg 
#           Df Sum Sq Mean Sq F value    Pr(>F)     
# cyl        1 817.71  817.71  79.561 6.113e-10 *** 
# Residuals 30 308.33   10.28 
# Signif. codes:  0 *** 0.001 ** 0.01 * 0.05 . 
# Plot the distribution 
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')

Код выдаст следующий результат -

Значение p, которое мы получаем в примере, значительно меньше 0,05, поэтому R возвращает символ '***', чтобы обозначить это. Это означает, что мы отвергаем нулевую гипотезу и обнаруживаем различия между средними значениями миль на галлон среди разных группcyl переменная.