Аналитика больших данных - Анализ временных рядов
Временные ряды - это последовательность наблюдений за категориальными или числовыми переменными, проиндексированными по дате или метке времени. Ярким примером данных временного ряда является временной ряд цены акции. В следующей таблице мы можем увидеть базовую структуру данных временных рядов. В этом случае наблюдения записываются каждый час.
| Отметка времени | Акции - Цена |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
Обычно первым шагом в анализе временных рядов является построение ряда, обычно это делается с помощью линейного графика.
Наиболее распространенное применение анализа временных рядов - это прогнозирование будущих значений числового значения с использованием временной структуры данных. Это означает, что доступные наблюдения используются для прогнозирования значений в будущем.
Временное упорядочение данных подразумевает, что традиционные методы регрессии бесполезны. Чтобы построить надежный прогноз, нам нужны модели, которые учитывают временной порядок данных.
Наиболее широко используемая модель для анализа временных рядов называется Autoregressive Moving Average(ARMA). Модель состоит из двух частей:autoregressive (AR) часть и moving average(MA) часть. Модель обычно называется моделью ARMA (p, q), где p - это порядок части авторегрессии, а q - порядок части скользящего среднего.
Модель авторегрессии
АР (р) читаются как модель авторегрессии порядка р. Математически это записывается как -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
где {φ 1 ,…, φ p } - параметры, которые необходимо оценить, c - константа, а случайная величина ε t представляет белый шум. Необходимы некоторые ограничения на значения параметров, чтобы модель оставалась неподвижной.
Скользящая средняя
Обозначение MA (q) относится к модели скользящего среднего порядка q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
где θ 1 , ..., θ q - параметры модели, μ - математическое ожидание X t , а ε t , ε t - 1 , ... - члены ошибки белого шума.
Авторегрессионное скользящее среднее
Модель ARMA (p, q) объединяет p членов авторегрессии и q членов скользящего среднего. Математически модель выражается следующей формулой -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Мы видим, что модель ARMA (p, q) представляет собой комбинацию моделей AR (p) и MA (q) .
Чтобы дать некоторое представление о модели, представьте, что часть AR уравнения пытается оценить параметры для X t - i наблюдений, чтобы предсказать значение переменной в X t . В конце концов, это средневзвешенное значение прошлых значений. В разделе МА используется тот же подход, но с ошибкой предыдущих наблюдений ε t - i . Итак, в итоге результат модели - это средневзвешенное значение.
Следующий фрагмент кода демонстрирует , как реализовать АРМА (P, Q) в R .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Построение графика данных обычно является первым шагом, чтобы выяснить, есть ли в данных временная структура. Из графика видно, что в конце каждого года бывают сильные всплески.
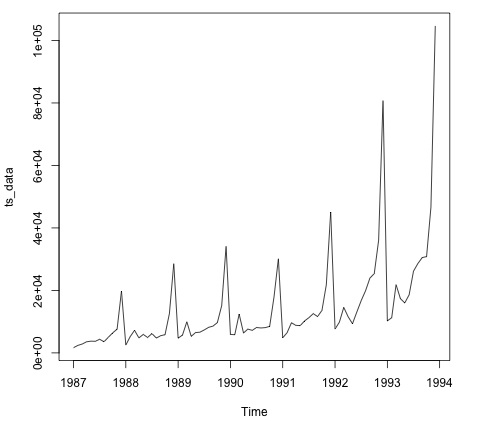
Следующий код соответствует модели ARMA для данных. Он запускает несколько комбинаций моделей и выбирает ту, которая имеет меньше ошибок.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172