DAA - самая длинная общая подпоследовательность

Самая длинная общая проблема подпоследовательности - найти самую длинную последовательность, которая существует в обеих данных строках.

Подпоследовательность

Рассмотрим последовательность S = <s ₁ , s ₂ , s ₃ , s ₄ ,…, s _n >.

Последовательность Z = <z ₁ , z ₂ , z ₃ , z ₄ ,…, z _m > над S называется подпоследовательностью S, если и только если она может быть получена из S удаления некоторых элементов.

Общая подпоследовательность

Предположим, X а также Yдве последовательности над конечным множеством элементов. Мы можем сказать чтоZ является общей подпоследовательностью X а также Y, если Z является подпоследовательностью обоих X а также Y.

Самая длинная общая подпоследовательность

Если задан набор последовательностей, самая длинная проблема общей подпоследовательности состоит в том, чтобы найти общую подпоследовательность для всех последовательностей, которая имеет максимальную длину.

Самая длинная общая проблема подпоследовательности - это классическая проблема информатики, основа программ сравнения данных, таких как утилита diff, и находящая применение в биоинформатике. Он также широко используется системами контроля версий, такими как SVN и Git, для согласования нескольких изменений, внесенных в коллекцию файлов, контролируемую версиями.

Наивный метод

Позволять X быть последовательностью длины m а также Y последовательность длины n. Проверьте каждую подпоследовательностьX является ли это подпоследовательностью Y, и вернуть самую длинную найденную общую подпоследовательность.

Есть 2^m подпоследовательности X. Проверка последовательностей на предмет того, является ли она подпоследовательностьюY берет O(n)время. Таким образом, наивный алгоритм взял быO(n2^m) время.

Динамическое программирование

Пусть X = <x ₁ , x ₂ , x ₃ ,…, x _m > и Y = <y ₁ , y ₂ , y ₃ ,…, y _n > - последовательности. Для вычисления длины элемента используется следующий алгоритм.

В этой процедуре таблица C[m, n] вычисляется в основном порядке строк, а другая таблица B[m,n] вычисляется для построения оптимального решения.

Algorithm: LCS-Length-Table-Formulation (X, Y)
m := length(X) 
n := length(Y) 
for i = 1 to m do 
   C[i, 0] := 0 
for j = 1 to n do 
   C[0, j] := 0 
for i = 1 to m do 
   for j = 1 to n do 
      if xi = yj 
         C[i, j] := C[i - 1, j - 1] + 1 
         B[i, j] := ‘D’ 
      else 
         if C[i -1, j] ≥ C[i, j -1] 
            C[i, j] := C[i - 1, j] + 1 
            B[i, j] := ‘U’ 
         else 
         C[i, j] := C[i, j - 1]
         B[i, j] := ‘L’ 
return C and B

Algorithm: Print-LCS (B, X, i, j)
if i = 0 and j = 0 
   return  
if B[i, j] = ‘D’ 
   Print-LCS(B, X, i-1, j-1) 
   Print(xi) 
else if B[i, j] = ‘U’ 
   Print-LCS(B, X, i-1, j) 
else 
   Print-LCS(B, X, i, j-1)

Этот алгоритм распечатает самую длинную общую подпоследовательность X а также Y.

Анализ

Чтобы заполнить таблицу, внешний for цикл повторяется m раз и внутренний for цикл повторяется nраз. Следовательно, сложность алгоритма O (m, n) , гдеm а также n - это длина двух струн.

пример

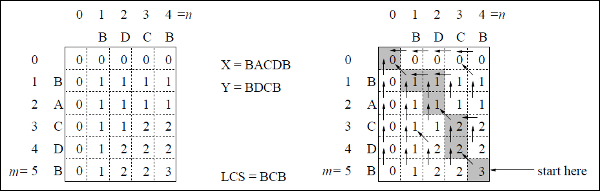
В этом примере у нас есть две строки X = BACDB а также Y = BDCB найти самую длинную общую подпоследовательность.

Следуя алгоритму LCS-Length-Table-Formulation (как указано выше), мы вычислили таблицу C (показанную слева) и таблицу B (показанную справа).

В таблице B вместо «D», «L» и «U» мы используем диагональную стрелку, стрелку влево и стрелку вверх соответственно. После создания таблицы B LCS определяется функцией LCS-Print. Результат - BCB.