DAA - многоступенчатый график
Многоступенчатый граф G = (V, E) ориентированный граф, в котором вершины разбиты на k (где k > 1) количество непересекающихся подмножеств S = {s1,s2,…,sk}такое, что ребро (u, v) находится в E, то u Є s i и v Є s 1 + 1 для некоторых подмножеств в разбиении и |s1| = |sk| = 1.
Вершина s Є s1 называется source и вершина t Є sk называется sink.
Gобычно считается взвешенным графом. В этом графе стоимость ребра (i, j) представлена как c (i, j) . Следовательно, стоимость пути от источникаs тонуть t сумма затрат каждого ребра на этом пути.
Задача многоступенчатого графа - найти путь с минимальными затратами из источника s тонуть t.
пример
Рассмотрим следующий пример, чтобы понять концепцию многоступенчатого графа.
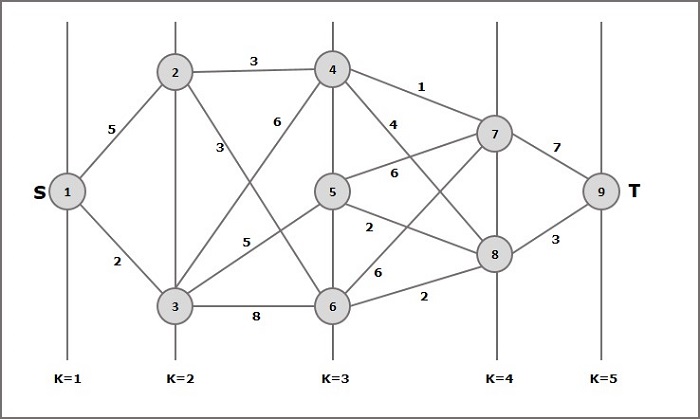
По формуле надо рассчитать стоимость (i, j) используя следующие шаги
Шаг-1: Стоимость (K-2, j)
На этом шаге три узла (узел 4, 5. 6) выбираются как j. Следовательно, у нас есть три варианта выбора минимальной стоимости на этом этапе.
Стоимость (3, 4) = min {c (4, 7) + Стоимость (7, 9), c (4, 8) + Стоимость (8, 9)} = 7
Стоимость (3, 5) = min {c (5, 7) + Стоимость (7, 9), c (5, 8) + Стоимость (8, 9)} = 5
Стоимость (3, 6) = min {c (6, 7) + Стоимость (7, 9), c (6, 8) + Стоимость (8, 9)} = 5
Шаг 2: Стоимость (K-3, j)
Два узла выбраны как j, потому что на этапе k - 3 = 2 есть два узла, 2 и 3. Итак, значение i = 2 и j = 2 и 3.
Стоимость (2, 2) = min {c (2, 4) + Стоимость (4, 8) + Стоимость (8, 9), c (2, 6) +
Стоимость (6, 8) + Стоимость (8, 9)} = 8
Стоимость (2, 3) = {c (3, 4) + Стоимость (4, 8) + Стоимость (8, 9), c (3, 5) + Стоимость (5, 8) + Стоимость (8, 9), c (3, 6) + Стоимость (6, 8) + Стоимость (8, 9)} = 10
Шаг 3: Стоимость (K-4, j)
Стоимость (1, 1) = {c (1, 2) + Стоимость (2, 6) + Стоимость (6, 8) + Стоимость (8, 9), c (1, 3) + Стоимость (3, 5) + Стоимость (5, 8) + Стоимость (8, 9))} = 12
c (1, 3) + Стоимость (3, 6) + Стоимость (6, 8 + Стоимость (8, 9))} = 13
Следовательно, путь с минимальной стоимостью равен 1→ 3→ 5→ 8→ 9.