DAA - Кратчайшие пути

Алгоритм Дейкстры

Алгоритм Дейкстры решает задачу поиска кратчайших путей с одним источником на ориентированном взвешенном графе G = (V, E) , где все ребра неотрицательны (т. Е. W (u, v) ≥ 0 для каждого ребра (u, v ) Є E ).

В следующем алгоритме мы будем использовать одну функцию Extract-Min(), который извлекает узел с наименьшим ключом.

Algorithm: Dijkstra’s-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
S := Ф 
Q := G.V 
while Q ≠ Ф 
   u := Extract-Min (Q) 
   S := S U {u} 
   for each vertex v Є G.adj[u] 
      if v.d > u.d + w(u, v) 
         v.d := u.d + w(u, v) 
         v.∏ := u

Анализ

Сложность этого алгоритма полностью зависит от реализации функции Extract-Min. Если функция extract min реализована с использованием линейного поиска, сложность этого алгоритма составляетO(V² + E).

В этом алгоритме, если мы используем min-heap, на котором Extract-Min() функция работает, чтобы вернуть узел из Q с наименьшим ключом сложность этого алгоритма может быть уменьшена еще больше.

пример

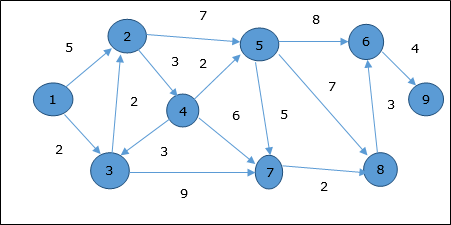
Рассмотрим вершину 1 а также 9в качестве начальной и целевой вершины соответственно. Первоначально все вершины, кроме начальной, отмечены знаком ∞, а начальная вершина отмечена знаком0.

Вершина	Начальная	Шаг 1 V 1	Шаг 2 V 3	Шаг 3 V 2	Step4 V 4	Шаг 5 V 5	Шаг 6 V 7	Step7 V 8	Step8 V 6
1	0	0	0	0	0	0	0	0	0
2	∞	5	4	4	4	4	4	4	4
3	∞	2	2	2	2	2	2	2	2
4	∞	∞	∞	7	7	7	7	7	7
5	∞	∞	∞	11	9	9	9	9	9
6	∞	∞	∞	∞	∞	17	17	16	16
7	∞	∞	11	11	11	11	11	11	11
8	∞	∞	∞	∞	∞	16	13	13	13
9	∞	∞	∞	∞	∞	∞	∞	∞	20

Следовательно, минимальное расстояние до вершины 9 из вершины 1 является 20. И путь

1 → 3 → 7 → 8 → 6 → 9

Этот путь определяется на основе информации предшественника.

Алгоритм Беллмана Форда

Этот алгоритм решает задачу поиска кратчайшего пути с одним источником ориентированного графа. G = (V, E)в котором веса ребер могут быть отрицательными. Более того, этот алгоритм можно применить для поиска кратчайшего пути, если не существует цикла с отрицательным весом.

Algorithm: Bellman-Ford-Algorithm (G, w, s) 
for each vertex v Є G.V  
   v.d := ∞ 
   v.∏ := NIL 
s.d := 0 
for i = 1 to |G.V| - 1 
   for each edge (u, v) Є G.E 
      if v.d > u.d + w(u, v) 
         v.d := u.d +w(u, v) 
         v.∏ := u 
for each edge (u, v) Є G.E 
   if v.d > u.d + w(u, v) 
      return FALSE 
return TRUE

Анализ

Первое for цикл используется для инициализации, которая выполняется в O(V)раз. Следующийfor цикл работает |V - 1| проходит по краям, что занимаетO(E) раз.

Следовательно, алгоритм Беллмана-Форда работает в O(V, E) время.

пример

В следующем примере показано, как работает алгоритм Беллмана-Форда, шаг за шагом. Этот граф имеет отрицательное ребро, но не имеет отрицательного цикла, поэтому проблему можно решить с помощью этой техники.

Во время инициализации все вершины, кроме источника, отмечены знаком ∞, а источник отмечен значком 0.

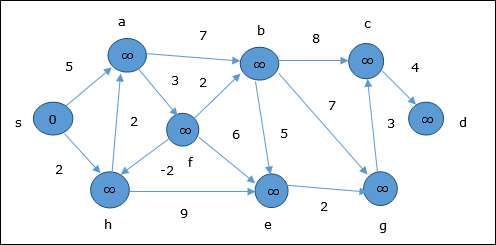
На первом этапе все вершины, достижимые из источника, обновляются с минимальной стоимостью. Следовательно, вершиныa а также h обновлены.

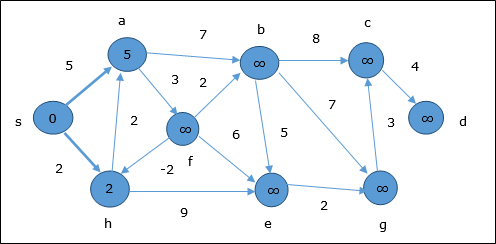
На следующем этапе вершины a, b, f а также e обновлены.

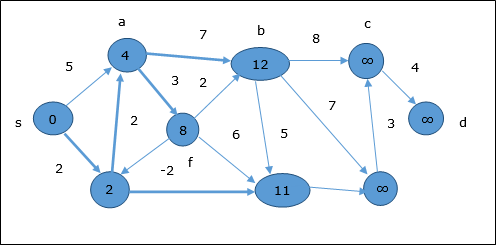
Следуя той же логике, на этом шаге вершины b, f, c а также g обновлены.

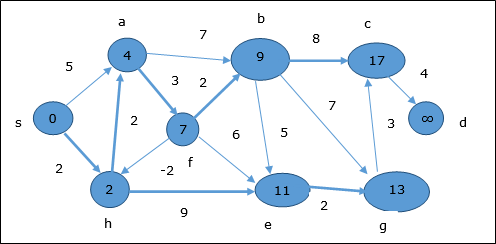
Здесь вершины c а также d обновлены.

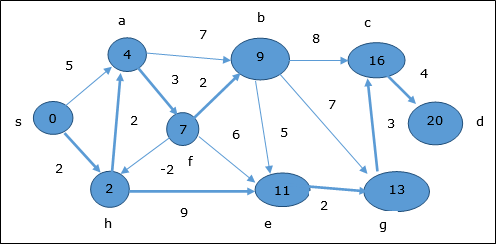
Следовательно, минимальное расстояние между вершинами s и вершина d является 20.

На основе информации предшественника путь s → h → e → g → c → d