NP Hard и NP-Complete классы
Проблема в классе NPC, если он в NP и как hardкак любая проблема в НП. Проблема в томNP-hard если все задачи в NP сводятся к нему за полиномиальное время, даже если это может не быть в самом NP.
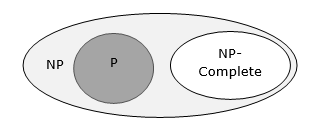
Если для любой из этих задач существует алгоритм с полиномиальным временем, все проблемы в NP будут разрешимы за полиномиальное время. Эти проблемы называютсяNP-complete. Феномен NP-полноты важен как с теоретической, так и с практической точки зрения.
Определение NP-полноты
Язык B является NP-complete если он удовлетворяет двум условиям
B находится в НП
Каждые A в NP полиномиальное время сводится к B.
Если язык удовлетворяет второму свойству, но не обязательно первому, язык B известен как NP-Hard. Неформально проблема поискаB является NP-Hard если есть какие-то NP-Complete проблема A что Тьюринг сводится к B.
Проблема в NP-Hard не может быть решена за полиномиальное время, пока P = NP. Если доказано, что проблема связана с NPC, нет необходимости тратить время на попытки найти эффективный алгоритм для ее решения. Вместо этого мы можем сосредоточиться на алгоритме аппроксимации проекта.
NP-полные задачи
Ниже приведены некоторые NP-Complete задачи, для которых не известен алгоритм с полиномиальным временем.
- Определение того, есть ли у графа гамильтонов цикл
- Определение выполнимости булевой формулы и т. Д.
NP-сложные задачи
Следующие проблемы являются NP-Hard
- Проблема выполнимости схем
- Установить обложку
- Крышка Vertex
- Задача коммивояжера
В этом контексте мы сейчас обсудим TSP - это NP-Complete.
TSP - это NP-Complete
Задача коммивояжера состоит из продавца и набора городов. Продавец должен посетить каждый из городов, начиная с определенного и возвращаясь в тот же город. Проблема в том, что коммивояжер хочет минимизировать общую продолжительность поездки.
Доказательство
Чтобы доказать TSP is NP-Complete, сначала нужно доказать, что TSP belongs to NP. В TSP мы находим тур и проверяем, содержит ли он каждую вершину один раз. Затем рассчитывается общая стоимость краев тура. Наконец, проверяем, минимальна ли стоимость. Это может быть выполнено за полиномиальное время. Таким образомTSP belongs to NP.
Во-вторых, мы должны доказать, что TSP is NP-hard. Чтобы доказать это, один из способов - показать, чтоHamiltonian cycle ≤p TSP (как мы знаем, проблема гамильтонова цикла NP-полна).
Предполагать G = (V, E) быть примером гамильтонова цикла.
Следовательно, создается экземпляр TSP. Создаем полный графG' = (V, E'), где
$$ E ^ {'} = \ lbrace (i, j) \ двоеточие i, j \ in V \: \: и \: i \ neq j $$
Таким образом, функция стоимости определяется следующим образом -
$$ t (i, j) = \ begin {cases} 0 & if \: (i, j) \: \ in E \\ 1 и в противном случае \ end {ases} $$
Теперь предположим, что гамильтонов цикл h существует в G. Понятно, что стоимость каждого ребра вh является 0 в G' поскольку каждое ребро принадлежит E. Следовательно,h имеет стоимость 0 в G'. Таким образом, если графG имеет гамильтонов цикл, то граф G' есть тур по 0 Стоимость.
Наоборот, мы предполагаем, что G' есть тур h' стоимости не более 0. Стоимость ребра вE' находятся 0 и 1по определению. Следовательно, каждое ребро должно иметь стоимость0 как стоимость h' является 0. Таким образом, мы заключаем, чтоh' содержит только ребра в E.
Таким образом, мы доказали, что G имеет гамильтонов цикл тогда и только тогда, когда G' имеет тур стоимостью не более 0. ТСП является NP-полным.