DAA - крышка Vertex

Вершина-покрытие неориентированного графа G = (V, E) это подмножество вершин V^' ⊆ V так что если край (u, v) край G, то либо u в V или же v в V^' или оба.

Найдите вершину-покрытие максимального размера в данном неориентированном графе. Это оптимальное вершинное покрытие является оптимизационной версией NP-полной задачи. Однако найти вершинное покрытие, близкое к оптимальному, не так уж и сложно.

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

пример

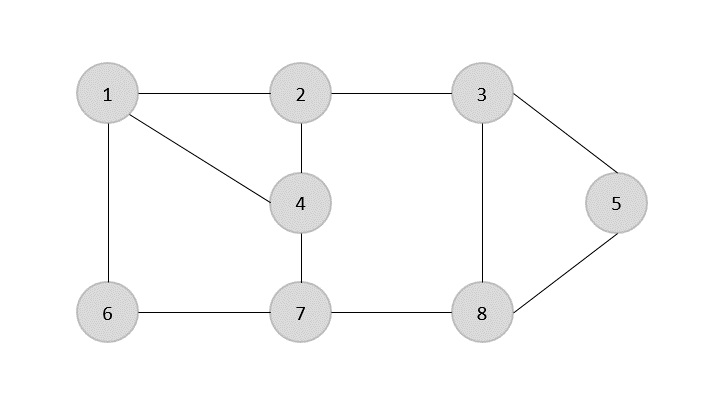
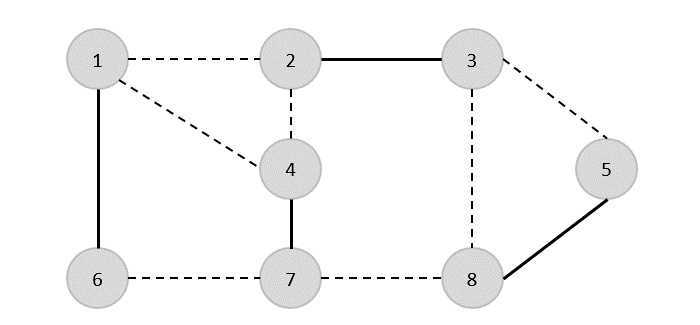
Множество ребер данного графа -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

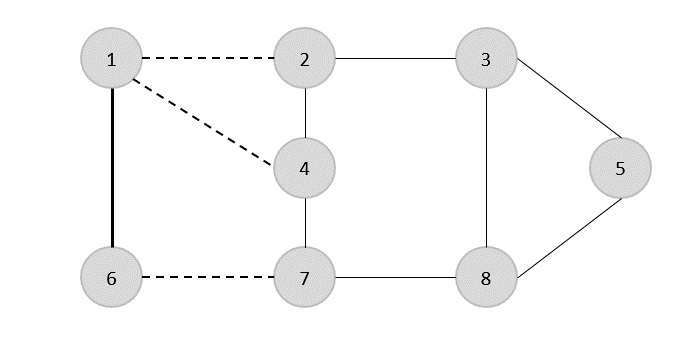
Теперь начнем с выбора произвольного ребра (1,6). Мы удаляем все ребра, инцидентные вершине 1 или 6, и добавляем ребро (1,6) для покрытия.

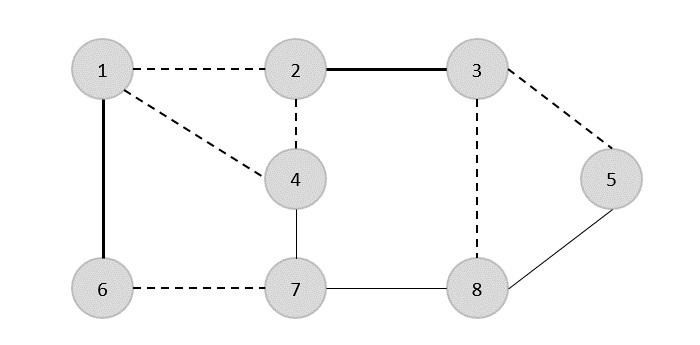
На следующем шаге мы случайным образом выбрали другое ребро (2,3).

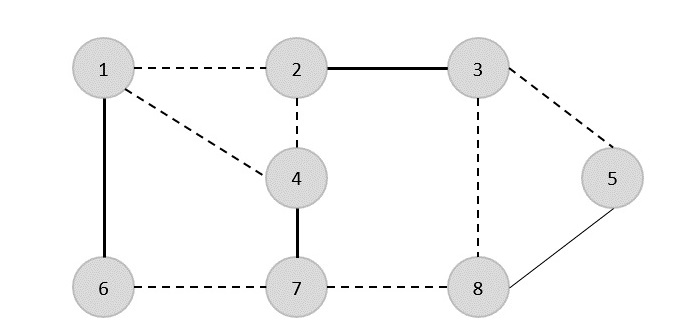
Теперь выбираем еще одно ребро (4,7).

Выбираем еще одно ребро (8,5).

Следовательно, вершинное покрытие этого графа равно {1,2,4,5}.

Анализ

Легко видеть, что время работы этого алгоритма равно O(V + E), используя список смежности для представления E^'.