การเชื่อมต่อวงจรในตัวเก็บประจุ
ในวงจรตัวเก็บประจุสามารถเชื่อมต่อแบบอนุกรมหรือแบบขนาน หากมีการเชื่อมต่อชุดตัวเก็บประจุในวงจรประเภทของการเชื่อมต่อตัวเก็บประจุจะเกี่ยวข้องกับค่าแรงดันและกระแสในเครือข่ายนั้น
ตัวเก็บประจุในซีรี่ส์
ให้เราสังเกตว่าเกิดอะไรขึ้นเมื่อมีการเชื่อมต่อตัวเก็บประจุเพียงไม่กี่ตัวในซีรี่ส์ ให้เราพิจารณาตัวเก็บประจุสามตัวที่มีค่าต่างกันดังแสดงในรูปด้านล่าง

ความจุ
เมื่อพิจารณาความจุของเครือข่ายที่มีตัวเก็บประจุอยู่ในอนุกรมจะมีการเพิ่มความจุซึ่งกันและกันของตัวเก็บประจุทั้งหมดเพื่อให้ได้ค่าความจุทั้งหมด เพื่อให้ชัดเจนยิ่งขึ้น
$$ \ frac {1} {C_ {T}} \: \: = \: \: \ frac {1} {C_ {1}} \: \: + \: \: \ frac {1} {C_ { 2}} \: \: + \: \: \ frac {1} {C_ {3}} $$
ตามสูตรเดียวกันหากมีการเชื่อมต่อตัวเก็บประจุเพียงสองตัวในอนุกรมกัน
$$ C_ {T} \: \: = \: \: \ frac {C_ {1} \: \: \ times \: \: C_ {2}} {C_ {1} \: \: + \: \ : C_ {2}} $$
ที่ไหน C 1คือความจุข้าม 1 เซนต์เก็บประจุ C 2คือความจุข้าม 2 ครั้งเก็บประจุและ C 3คือความจุข้าม 3 ถประจุอยู่ในเครือข่ายดังกล่าวข้างต้น
แรงดันไฟฟ้า
แรงดันไฟฟ้าของตัวเก็บประจุแต่ละตัวขึ้นอยู่กับค่าของความจุแต่ละตัว ซึ่งหมายความว่า
$$ V_ {C1} \: \: = \: \: \ frac {Q_ {T}} {C_ {1}} \: \: V_ {C2} \: \: = \: \: \ frac {Q_ {T}} {C_ {2}} \: \: V_ {C3} \: \: = \: \: \ frac {Q_ {T}} {C_ {3}} $$
แรงดันไฟฟ้ารวมในวงจรตัวเก็บประจุแบบอนุกรม
$$ V_ {T} \: \: = \: \: V_ {C1} \: \: + \: \: V_ {C2} \: \: + \: \: V_ {C3} $$
โดยที่ V c1เป็นแรงดันไฟฟ้าทั่ว 1 เซนต์เก็บประจุ V c2เป็นแรงดันไฟฟ้าใน 2 ครั้งเก็บประจุและ V c3เป็นแรงดันไฟฟ้าทั่ว 3 ถประจุอยู่ในเครือข่ายดังกล่าวข้างต้น
ปัจจุบัน
จำนวนกระแสทั้งหมดที่ไหลผ่านชุดตัวเก็บประจุที่เชื่อมต่อเป็นอนุกรมจะเท่ากันทุกจุด ดังนั้นตัวเก็บประจุจะเก็บประจุในปริมาณเท่ากันโดยไม่คำนึงถึงค่าความจุ
ปัจจุบันผ่านเครือข่าย
$$ ฉัน \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
โดยที่ I 1คือกระแสผ่านตัวเก็บประจุ1 st , I 2คือกระแสผ่านตัวเก็บประจุ2 ndและ I 3คือกระแสผ่านตัวเก็บประจุ3 rdในเครือข่ายด้านบน
เนื่องจากกระแสเท่ากันการจัดเก็บประจุจะเหมือนกันเนื่องจากแผ่นใด ๆ ของตัวเก็บประจุได้รับประจุจากตัวเก็บประจุที่อยู่ติดกันดังนั้นตัวเก็บประจุในอนุกรมจะมีประจุเท่ากัน
$$ Q_ {T} \: \: = \: \: Q_ {1} \: \: = \: \: Q_ {2} \: \: = \: \: Q_ {3} $$
ตัวเก็บประจุแบบขนาน
ให้เราสังเกตว่าเกิดอะไรขึ้นเมื่อเชื่อมต่อตัวเก็บประจุไม่กี่ตัวในแบบขนาน ให้เราพิจารณาตัวเก็บประจุสามตัวที่มีค่าต่างกันดังแสดงในรูปด้านล่าง
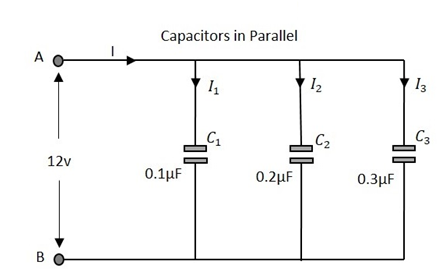
ความจุ
ความจุรวมของวงจรเทียบเท่ากับผลรวมของความจุแต่ละตัวของตัวเก็บประจุในเครือข่าย
$$ C_ {T} \: \: = \: \: C_ {1} \: \: + \: \: C_ {2} \: \: + \: \: C_ {3} $$
ที่ไหน C 1คือความจุข้าม 1 เซนต์เก็บประจุ C 2คือความจุข้าม 2 ครั้งเก็บประจุและ C 3คือความจุข้าม 3 ถประจุอยู่ในเครือข่ายดังกล่าวข้างต้น
แรงดันไฟฟ้า
แรงดันไฟฟ้าที่วัดได้ที่ส่วนท้ายของวงจรคือ same เป็นแรงดันไฟฟ้าของตัวเก็บประจุทั้งหมดที่เชื่อมต่อในวงจรขนาน
$$ V_ {T} \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
โดยที่ V c1เป็นแรงดันไฟฟ้าทั่ว 1 เซนต์เก็บประจุ V c2เป็นแรงดันไฟฟ้าใน 2 ครั้งเก็บประจุและ V c3เป็นแรงดันไฟฟ้าทั่ว 3 ถประจุอยู่ในเครือข่ายดังกล่าวข้างต้น
ปัจจุบัน
กระแสรวมที่ไหลเท่ากับผลรวมของกระแสที่ไหลผ่านตัวเก็บประจุแต่ละตัวที่เชื่อมต่อในเครือข่ายแบบขนาน
$$ I_ {T} \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
โดยที่ I 1คือกระแสผ่านตัวเก็บประจุ1 st , I 2คือกระแสผ่านตัวเก็บประจุ2 ndและ I 3คือกระแสผ่านตัวเก็บประจุ3 rdในเครือข่ายด้านบน