การเชื่อมต่อวงจรในตัวเหนี่ยวนำ
ตัวเหนี่ยวนำเมื่อเชื่อมต่อในวงจรการเชื่อมต่อนั้นอาจเป็นแบบอนุกรมหรือขนานก็ได้ แจ้งให้เราทราบว่าจะเกิดอะไรขึ้นกับค่ากระแสไฟฟ้าและค่าความต้านทานทั้งหมดหากเชื่อมต่อเป็นอนุกรมด้วยเมื่อเชื่อมต่อแบบขนาน
ตัวเหนี่ยวนำในซีรี่ส์
ให้เราสังเกตสิ่งที่เกิดขึ้นเมื่อมีการเชื่อมต่อตัวเหนี่ยวนำเพียงไม่กี่ตัวในซีรี่ส์ ให้เราพิจารณาตัวต้านทานสามตัวที่มีค่าต่างกันดังแสดงในรูปด้านล่าง
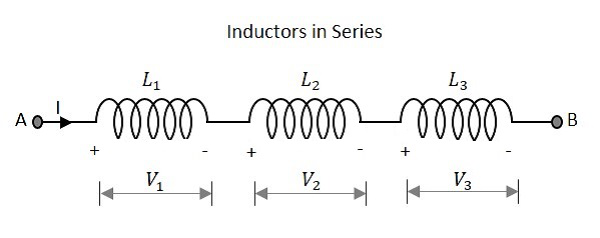
ตัวเหนี่ยวนำ
ค่าความเหนี่ยวนำทั้งหมดของวงจรที่มีตัวเหนี่ยวนำแบบอนุกรมเท่ากับผลรวมของตัวเหนี่ยวนำแต่ละตัว ค่าความเหนี่ยวนำทั้งหมดของเครือข่ายที่ระบุข้างต้นคือ
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
โดยที่ L 1เป็นตัวเหนี่ยวนำของตัวต้านทาน1 st , L 2คือตัวเหนี่ยวนำของตัวต้านทาน2 ndและ L 3คือตัวเหนี่ยวนำของตัวต้านทาน3 rdในเครือข่ายด้านบน
แรงดันไฟฟ้า
แรงดันไฟฟ้าทั้งหมดที่ปรากฏในเครือข่ายตัวเหนี่ยวนำแบบอนุกรมคือการเพิ่มแรงดันตกที่ตัวเหนี่ยวนำแต่ละตัว
แรงดันไฟฟ้าทั้งหมดที่ปรากฏในวงจร
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
โดยที่ V 1เป็นแรงดันไฟฟ้าตกข้าม 1 เซนต์เหนี่ยวนำ, V 2เป็นแรงดันไฟฟ้าตกข้าม 2 ครั้งที่เหนี่ยวนำและ V 3เป็นแรงดันไฟฟ้าตกข้าม 3 ถเหนี่ยวนำในเครือข่ายดังกล่าวข้างต้น
ปัจจุบัน
จำนวนกระแสทั้งหมดที่ไหลผ่านชุดของตัวเหนี่ยวนำที่เชื่อมต่อแบบอนุกรมจะเท่ากันทุกจุดทั่วทั้งเครือข่าย
กระแสผ่านเครือข่าย
$$ ฉัน \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
ฉัน1เป็นปัจจุบันผ่าน 1 เซนต์เหนี่ยวนำผม2ที่เป็นปัจจุบันผ่าน 2 ครั้งที่เหนี่ยวนำและฉัน3เป็นปัจจุบันผ่าน 3 ถเหนี่ยวนำในเครือข่ายดังกล่าวข้างต้น
ตัวเหนี่ยวนำแบบขนาน
ให้เราสังเกตว่าเกิดอะไรขึ้นเมื่อตัวต้านทานไม่กี่ตัวเชื่อมต่อแบบขนาน ให้เราพิจารณาตัวต้านทานสามตัวที่มีค่าต่างกันดังแสดงในรูปด้านล่าง

ตัวเหนี่ยวนำ
ค่าความเหนี่ยวนำทั้งหมดของวงจรที่มีตัวต้านทานแบบขนานคำนวณได้แตกต่างจากวิธีเครือข่ายตัวเหนี่ยวนำแบบอนุกรม ที่นี่ค่าซึ่งกันและกัน (1 / R) ของตัวเหนี่ยวนำแต่ละตัวจะถูกเพิ่มด้วยผกผันของผลรวมพีชคณิตเพื่อให้ได้ค่าตัวเหนี่ยวนำทั้งหมด
ค่าความเหนี่ยวนำทั้งหมดของเครือข่ายคือ
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
โดยที่ L 1คือความเหนี่ยวนำของตัวเหนี่ยวนำ 1 st , L 2คือความเหนี่ยวนำของตัวเหนี่ยวนำ 2 ndและ L 3คือตัวเหนี่ยวนำของตัวเหนี่ยวนำ 3 rdในเครือข่ายด้านบน
จากวิธีการที่เรามีในการคำนวณการเหนี่ยวนำแบบขนานเราสามารถหาสมการง่ายๆสำหรับเครือข่ายขนานสองตัวเหนี่ยวนำได้ มันคือ
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
แรงดันไฟฟ้า
แรงดันไฟฟ้าทั้งหมดที่ปรากฏบนเครือข่ายตัวเหนี่ยวนำแบบขนานจะเหมือนกับแรงดันตกที่ตัวเหนี่ยวนำแต่ละตัว
แรงดันไฟฟ้าที่ปรากฏในวงจร
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
โดยที่ V 1เป็นแรงดันไฟฟ้าตกข้าม 1 เซนต์เหนี่ยวนำ, V 2เป็นแรงดันไฟฟ้าตกข้าม 2 ครั้งที่เหนี่ยวนำและ V 3เป็นแรงดันไฟฟ้าตกข้าม 3 ถเหนี่ยวนำในเครือข่ายดังกล่าวข้างต้น ดังนั้นแรงดันไฟฟ้าจะเท่ากันทุกจุดของเครือข่ายตัวเหนี่ยวนำแบบขนาน
ปัจจุบัน
จำนวนกระแสทั้งหมดที่เข้าสู่เครือข่ายอุปนัยแบบขนานคือผลรวมของกระแสแต่ละกระแสที่ไหลในสาขาขนานทั้งหมด ค่าความเหนี่ยวนำของแต่ละสาขาจะกำหนดมูลค่าของกระแสที่ไหลผ่าน
กระแสรวมผ่านเครือข่ายคือ
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
ฉัน1เป็นปัจจุบันผ่าน 1 เซนต์เหนี่ยวนำผม2ที่เป็นปัจจุบันผ่าน 2 ครั้งที่เหนี่ยวนำและฉัน3เป็นปัจจุบันผ่าน 3 ถเหนี่ยวนำในเครือข่ายดังกล่าวข้างต้น
ดังนั้นผลรวมของแต่ละกระแสในสาขาต่างๆจะได้รับกระแสรวมในเครือข่ายคู่ขนาน
ปฏิกิริยาอุปนัย
ปฏิกิริยาอุปนัยคือการต่อต้านที่นำเสนอโดยตัวเหนี่ยวนำต่อการไหลของกระแสสลับหรือเพียงแค่กระแสไฟฟ้ากระแสสลับ ตัวเหนี่ยวนำมีคุณสมบัติในการต่อต้านการเปลี่ยนแปลงของการไหลของกระแสและด้วยเหตุนี้จึงแสดงการต่อต้านซึ่งสามารถเรียกได้ว่าเป็นreactanceเนื่องจากควรพิจารณาความถี่ของกระแสอินพุตพร้อมกับความต้านทานที่เสนอด้วย
บ่งชี้ - XL
หน่วย - Ohms
สัญลักษณ์ - Ω
ในวงจรอุปนัยอย่างหมดจดกระแส IL lagsแรงดันไฟฟ้าที่ใช้ 90 ° รีแอคแตนซ์อุปนัยคำนวณโดย
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
โดยที่ f คือความถี่ของสัญญาณ ดังนั้นรีแอคแตนซ์อุปนัยจึงเป็นฟังก์ชันของความถี่และความเหนี่ยวนำ