Fuzzy Logic - ทฤษฎีเซตคลาสสิก

ก setเป็นคอลเลกชันที่ไม่เรียงลำดับขององค์ประกอบต่างๆ สามารถเขียนอย่างชัดเจนโดยแสดงรายการองค์ประกอบโดยใช้วงเล็บชุด หากลำดับขององค์ประกอบมีการเปลี่ยนแปลงหรือมีการทำซ้ำองค์ประกอบใด ๆ ของชุดจะไม่ทำการเปลี่ยนแปลงใด ๆ ในชุด

ตัวอย่าง

ชุดของจำนวนเต็มบวกทั้งหมด
ชุดของดาวเคราะห์ทั้งหมดในระบบสุริยะ
ชุดของรัฐทั้งหมดในอินเดีย
ชุดตัวอักษรพิมพ์เล็กทั้งหมดของตัวอักษร

การแทนค่าทางคณิตศาสตร์ของเซต

ชุดสามารถแสดงได้สองวิธี -

บัญชีรายชื่อหรือรูปแบบตาราง

ในรูปแบบนี้ชุดจะแสดงโดยการแสดงรายการองค์ประกอบทั้งหมดที่ประกอบด้วยชุดนั้น องค์ประกอบจะอยู่ภายในวงเล็บปีกกาและคั่นด้วยเครื่องหมายจุลภาค

ต่อไปนี้เป็นตัวอย่างของชุดในบัญชีรายชื่อหรือรูปแบบตาราง -

ชุดเสียงสระในตัวอักษรภาษาอังกฤษ A = {a, e, i, o, u}
ชุดเลขคี่น้อยกว่า 10, B = {1,3,5,7,9}

ตั้งค่าสัญกรณ์ตัวสร้าง

ในรูปแบบนี้ชุดจะถูกกำหนดโดยการระบุคุณสมบัติที่องค์ประกอบของชุดมีเหมือนกัน ชุดนี้อธิบายว่า A = {x: p (x)}

Example 1 - ชุด {a, e, i, o, u} เขียนเป็น

A = {x: x เป็นสระในตัวอักษรภาษาอังกฤษ}

Example 2 - ชุด {1,3,5,7,9} เขียนเป็น

B = {x: 1 ≤ x <10 และ (x% 2) ≠ 0}

ถ้าองค์ประกอบ x เป็นสมาชิกของเซต S ใด ๆ มันจะแสดงด้วยx∈Sและถ้าองค์ประกอบ y ไม่ใช่สมาชิกของเซต S องค์ประกอบนั้นจะแสดงด้วย y .S

Example - ถ้า S = {1,1.2,1.7,2}, 1 ∈ S แต่ 1.5 ∉ S

Cardinality ของชุด

จำนวนองค์ประกอบของเซต S แสดงโดย | S || S | คือจำนวนองค์ประกอบของเซต หมายเลขนี้เรียกอีกอย่างว่าหมายเลขคาร์ดินัล หากเซตมีองค์ประกอบจำนวนไม่ จำกัด จำนวนองค์ประกอบจะเท่ากับ∞∞

Example- | {1,4,3,5} | = 4, | {1,2,3,4,5, …} | = ∞

หากมีสองชุด X และ Y | X | = | Y | หมายถึงชุด X และ Y สองชุดที่มีความสำคัญเท่ากัน เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X เท่ากับจำนวนองค์ประกอบใน Y ในกรณีนี้มีฟังก์ชัน bijective 'f' จาก X ถึง Y

| X | ≤ | Y | หมายถึงว่าเซ็ตคาร์ดินาลลิตี้ของ X น้อยกว่าหรือเท่ากับเซ็ตคาร์ดินาลลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่าหรือเท่ากับ Y ที่นี่มีฟังก์ชันฉีด 'f' จาก X ถึง Y

| X | <| Y | หมายถึงคาร์ดินาลลิตี้ของเซต X น้อยกว่าเซ็ตคาร์ดินาลิตี้ของ Y เกิดขึ้นเมื่อจำนวนองค์ประกอบใน X น้อยกว่า Y ในที่นี้ฟังก์ชั่น 'f' จาก X ถึง Y เป็นฟังก์ชั่นการฉีด แต่ไม่ใช่ bijective

ถ้า| X | ≤ | Y | และ| X | ≤ | Y | แล้ว| X | = | Y | . ชุด X และ Y มักเรียกกันว่าequivalent sets.

ประเภทของชุด

ชุดสามารถแบ่งออกเป็นหลายประเภท ซึ่งบางส่วนเป็นแบบ จำกัด , ไม่มีที่สิ้นสุด, เซตย่อย, สากล, เหมาะสม, เซตซิงเกิลตัน ฯลฯ

ชุดไฟไนต์

ชุดที่มีจำนวนองค์ประกอบที่แน่นอนเรียกว่าเซต จำกัด

Example - S = {x | x ∈ N และ 70> x> 50}

ชุดไม่มีที่สิ้นสุด

ชุดที่มีองค์ประกอบจำนวนไม่ จำกัด เรียกว่าเซตไม่มีที่สิ้นสุด

Example - S = {x | x ∈ N และ x> 10}

ชุดย่อย

เซต X คือเซตย่อยของเซต Y (เขียนเป็น X ⊆ Y) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y

Example 1- ให้ X = {1,2,3,4,5,6} และ Y = {1,2} เซต Y เป็นเซตย่อยของเซต X เนื่องจากองค์ประกอบทั้งหมดของเซต Y อยู่ในเซต X ดังนั้นเราจึงเขียนY⊆Xได้

Example 2- ให้ X = {1,2,3} และ Y = {1,2,3} เซต Y เป็นเซตย่อย (ไม่ใช่เซตย่อยที่เหมาะสม) ของเซต X เนื่องจากองค์ประกอบทั้งหมดของเซต Y อยู่ในเซต X ดังนั้นเราจึงเขียนY⊆Xได้

ชุดย่อยที่เหมาะสม

คำว่า "ชุดย่อยที่เหมาะสม" สามารถกำหนดเป็น "ชุดย่อย แต่ไม่เท่ากับ" เซต X เป็นเซตย่อยที่เหมาะสมของเซต Y (เขียนเป็น X ⊂ Y) ถ้าทุกองค์ประกอบของ X เป็นองค์ประกอบของเซต Y และ | X | <| Y |.

Example- ให้ X = {1,2,3,4,5,6} และ Y = {1,2} ที่นี่ตั้งค่า Y ⊂ X เนื่องจากองค์ประกอบทั้งหมดใน Y มีอยู่ใน X ด้วยและ X ก็มีอย่างน้อยหนึ่งองค์ประกอบที่มากกว่าชุด Y

ชุดสากล

เป็นการรวบรวมองค์ประกอบทั้งหมดในบริบทหรือแอปพลิเคชันเฉพาะ ชุดทั้งหมดในบริบทหรือแอปพลิเคชันนั้นเป็นส่วนย่อยของชุดสากลนี้ ชุดสากลแสดงเป็น U

Example- เราอาจกำหนด U เป็นเซตของสัตว์ทั้งหมดบนโลก ในกรณีนี้ชุดของสัตว์เลี้ยงลูกด้วยนมทั้งหมดเป็นเซตย่อยของ U ชุดของปลาทั้งหมดเป็นเซตย่อยของ U ชุดของแมลงทั้งหมดเป็นเซตย่อยของ U และอื่น ๆ

ชุดว่างหรือชุดค่าว่าง

ชุดว่างไม่มีองค์ประกอบ แสดงโดยΦ เนื่องจากจำนวนองค์ประกอบในเซตว่างมีจำนวน จำกัด เซตว่างจึงเป็นเซต จำกัด จำนวนเต็มของเซตว่างหรือเซตว่างเป็นศูนย์

Example - S = {x | x ∈ N และ 7 <x <8} = Φ

Singleton Set หรือ Unit Set

ชุด Singleton หรือชุดหน่วยประกอบด้วยองค์ประกอบเดียว ชุดซิงเกิลตันแสดงด้วย {s}

Example - S = {x | x ∈ N, 7 <x <9} = {8}

ชุดที่เท่ากัน

ถ้าสองชุดมีองค์ประกอบเดียวกันก็จะถือว่าเท่ากัน

Example - ถ้า A = {1,2,6} และ B = {6,1,2} จะมีค่าเท่ากันทุกองค์ประกอบของเซต A คือองค์ประกอบของเซต B และทุกองค์ประกอบของเซต B เป็นองค์ประกอบของเซต A

ชุดที่เทียบเท่า

ถ้าความสำคัญของสองชุดเหมือนกันจะเรียกว่าชุดที่เท่ากัน

Example- ถ้า A = {1,2,6} และ B = {16,17,22} จะเทียบเท่ากับคาร์ดินาลลิตี้ของ A เท่ากับคาร์ดินาลลิตี้ของ B คือ | A | = | B | = 3

ชุดที่ทับซ้อนกัน

สองชุดที่มีองค์ประกอบร่วมอย่างน้อยหนึ่งชุดเรียกว่าชุดที่ทับซ้อนกัน กรณีชุดทับ -

$$ n \ left (A \ cup B \ right) = n \ left (A \ right) + n \ left (B \ right) - n \ left (A \ cap B \ right) $$

$$ n \ left (A \ cup B \ right) = n \ left (AB \ right) + n \ left (BA \ right) + n \ left (A \ cap B \ right) $$

$$ n \ left (A \ right) = n \ left (AB \ right) + n \ left (A \ cap B \ right) $$

$$ n \ left (B \ right) = n \ left (BA \ right) + n \ left (A \ cap B \ right) $$

Example- ให้, A = {1,2,6} และ B = {6,12,42} มีองค์ประกอบทั่วไป '6' ดังนั้นชุดเหล่านี้จึงเป็นชุดที่ทับซ้อนกัน

ชุดไม่ปะติดปะต่อ

ชุด A และ B สองชุดเรียกว่าชุดที่ไม่ปะติดปะต่อกันหากไม่มีองค์ประกอบที่เหมือนกันแม้แต่ชิ้นเดียว ดังนั้นชุดที่ไม่ปะติดปะต่อจึงมีคุณสมบัติดังต่อไปนี้ -

$$ n \ left (A \ cap B \ right) = \ phi $$

$$ n \ left (A \ cup B \ right) = n \ left (A \ right) + n \ left (B \ right) $$

Example - ให้ A = {1,2,6} และ B = {7,9,14} ไม่มีองค์ประกอบร่วมกันดังนั้นเซตเหล่านี้จึงเป็นเซตที่ทับซ้อนกัน

การดำเนินการกับชุดคลาสสิก

การดำเนินการชุดประกอบด้วย Set Union, Set Intersection, Set Difference, Complement of Set และ Cartesian Product

สหภาพ

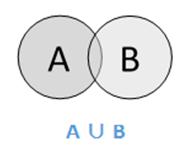
การรวมกันของเซต A และ B (แสดงโดย A ∪ BA ∪ B) คือเซตขององค์ประกอบที่อยู่ใน A ใน B หรือทั้ง A และ B ดังนั้น A ∪ B = {x | x ∈ A หรือ x ∈ B}

Example - ถ้า A = {10,11,12,13} และ B = {13,14,15} ดังนั้น A ∪ B = {10,11,12,13,14,15} - องค์ประกอบทั่วไปจะเกิดขึ้นเพียงครั้งเดียว

ทางแยก

จุดตัดของเซต A และ B (แสดงโดย A ∩ B) คือเซตขององค์ประกอบที่อยู่ในทั้ง A และ B ดังนั้น A ∩ B = {x | x ∈ A AND x ∈ B}

ความแตกต่าง / ส่วนเสริมสัมพัทธ์

ความแตกต่างของเซต A และ B (แสดงด้วย A-B) คือเซตขององค์ประกอบที่อยู่ใน A เท่านั้น แต่ไม่ใช่ใน B ดังนั้น A - B = {x | x ∈ A AND x ∉ B}

Example- ถ้า A = {10,11,12,13} และ B = {13,14,15} ดังนั้น (A - B) = {10,11,12} และ (B - A) = {14,15} . ที่นี่เราจะเห็น (A - B) ≠ (B - A)

ส่วนเสริมของชุด

ส่วนประกอบของเซต A (แสดงโดย A ′) คือชุดขององค์ประกอบที่ไม่อยู่ในเซต A ดังนั้น A′ = {x | x ∉ A}

โดยเฉพาะอย่างยิ่ง A ′= (U − A) โดยที่ U เป็นเซตสากลที่มีวัตถุทั้งหมด

Example - ถ้า A = {x | x เป็นของเซตของจำนวนเต็มเพิ่ม} ดังนั้น A ′= {y | y ไม่ได้อยู่ในเซตของจำนวนเต็มคี่}

ผลิตภัณฑ์คาร์ทีเซียน / ผลิตภัณฑ์ข้าม

ผลคูณคาร์ทีเซียนของ n จำนวนเซต A1, A2, …แสดงเป็น A1 × A2 ... × An สามารถกำหนดให้เป็นคู่ลำดับที่เป็นไปได้ทั้งหมด (x1, x2, … xn) โดยที่ x1 ∈ A1, x2 ∈ A2, … xn ∈ An

Example - ถ้าเราใช้สองเซต A = {a, b} และ B = {1,2}

ผลคูณคาร์ทีเซียนของ A และ B เขียนเป็น - A × B = {(a, 1), (a, 2), (b, 1), (b, 2)}

และผลคูณคาร์ทีเซียนของ B และ A เขียนเป็น - B × A = {(1, a), (1, b), (2, a), (2, b)}