RADAR เป็นระบบตรวจจับที่ใช้แม่เหล็กไฟฟ้าซึ่งทำงานโดยการแผ่คลื่นแม่เหล็กไฟฟ้าแล้วศึกษาเสียงสะท้อนหรือคลื่นสะท้อนกลับ

รูปแบบเต็มของ RADAR คือ RAดิโอ Detection And Ranging. การตรวจจับหมายถึงเป้าหมายว่ามีอยู่หรือไม่ เป้าหมายสามารถอยู่นิ่งหรือเคลื่อนย้ายได้เช่นไม่อยู่นิ่ง ช่วงหมายถึงระยะห่างระหว่างเรดาร์และเป้าหมาย

เรดาร์สามารถใช้สำหรับการใช้งานที่หลากหลายบนพื้นดินบนทะเลและในอวกาศ applications ของ Radars แสดงอยู่ด้านล่าง

• การควบคุมการจราจรทางอากาศ
• ความปลอดภัยของเรือ
• การตรวจจับสถานที่ห่างไกล
• การใช้งานทางทหาร

ในการใช้ Radar ใด ๆ หลักการพื้นฐานยังคงเหมือนเดิม ตอนนี้ให้เราพูดถึงหลักการของเรดาร์

หลักการพื้นฐานของเรดาร์

เรดาร์ใช้สำหรับตรวจจับวัตถุและค้นหาตำแหน่งของพวกมัน เราสามารถเข้าใจไฟล์basic principle ของเรดาร์จากรูปต่อไปนี้

ดังแสดงในรูปเรดาร์ส่วนใหญ่ประกอบด้วยตัวส่งและตัวรับ ใช้เสาอากาศเดียวกันสำหรับการส่งและรับสัญญาณ ฟังก์ชั่นของtransmitter คือการส่งสัญญาณเรดาร์ในทิศทางของเป้าหมายที่ปรากฏ

เป้าหมายสะท้อนสัญญาณที่ได้รับนี้ในทิศทางต่างๆ สัญญาณซึ่งสะท้อนกลับไปที่เสาอากาศจะได้รับจากไฟล์receiver.

คำศัพท์ของระบบเรดาร์

ต่อไปนี้เป็นคำศัพท์พื้นฐานซึ่งมีประโยชน์ในบทช่วยสอนนี้

• Range
• ความถี่ในการทำซ้ำของพัลส์
• ช่วงสูงสุดที่ไม่ชัดเจน
• ช่วงต่ำสุด

ตอนนี้ให้เราพูดคุยเกี่ยวกับคำศัพท์พื้นฐานเหล่านี้ทีละคำ

พิสัย

ระยะห่างระหว่างเรดาร์และเป้าหมายถูกเรียก Range ของเป้าหมายหรือเพียงแค่ช่วง R เรารู้ว่าเรดาร์ส่งสัญญาณไปยังเป้าหมายและเป้าหมายจึงส่งสัญญาณสะท้อนไปยังเรดาร์ด้วยความเร็วแสง C.

ปล่อยให้เวลาที่สัญญาณเดินทางจากเรดาร์ไปยังเป้าหมายและกลับไปที่เรดาร์เป็น 'T' ระยะทางสองทางระหว่างเรดาร์และเป้าหมายจะเท่ากับ 2R เนื่องจากระยะห่างระหว่างเรดาร์และเป้าหมายคือ R

ตอนนี้ต่อไปนี้เป็นสูตรสำหรับ Speed.

$$Speed= \frac{Distance}{Time}$$

$$\Rightarrow Distance=Speed\times Time$$

$$\Rightarrow 2R=C\times T$$

$$R=\frac{CT}{2}\:\:\:\:\:Equation\:1$$

เราสามารถค้นหาไฟล์ range of the target โดยการแทนค่าของ C & T ในสมการ 1

ความถี่ในการทำซ้ำของพัลส์

ควรส่งสัญญาณเรดาร์ทุกพัลส์นาฬิกา ควรเลือกระยะเวลาระหว่างพัลส์นาฬิกาทั้งสองให้เหมาะสมเพื่อให้ได้รับสัญญาณสะท้อนที่สอดคล้องกับพัลส์นาฬิกาปัจจุบันก่อนพัลส์นาฬิกาถัดไป โดยทั่วไปRadar wave form แสดงดังรูปต่อไปนี้

ดังแสดงในรูปเรดาร์ส่งสัญญาณเป็นระยะ มันมีชุดของพัลส์รูปสี่เหลี่ยมผืนผ้าแคบ ๆ เรียกช่วงเวลาระหว่างพัลส์นาฬิกาที่ต่อเนื่องกันpulse repetition time, $T_P$.

เรียกเวลาการทำซ้ำของพัลส์ซึ่งกันและกัน pulse repetition frequency, $f_P$. ในทางคณิตศาสตร์สามารถแสดงเป็น

$$f_P=\frac{1}{T_P}\:\:\:\:\:Equation\:2$$

ดังนั้นความถี่ในการทำซ้ำของพัลส์จึงไม่มีอะไรนอกจากความถี่ที่เรดาร์ส่งสัญญาณ

ช่วงสูงสุดที่ไม่ชัดเจน

เรารู้ว่าควรส่งสัญญาณเรดาร์ทุกพัลส์นาฬิกา หากเราเลือกระยะเวลาที่สั้นลงระหว่างพัลส์นาฬิกาสองครั้งสัญญาณสะท้อนที่สอดคล้องกับพัลส์นาฬิกาปัจจุบันจะได้รับหลังจากพัลส์นาฬิกาถัดไป ด้วยเหตุนี้ช่วงของเป้าหมายจึงเล็กกว่าช่วงจริง

ดังนั้นเราต้องเลือกระยะเวลาระหว่างพัลส์นาฬิกาสองครั้งเพื่อให้ได้รับสัญญาณสะท้อนที่ตรงกับพัลส์นาฬิกาปัจจุบันก่อนที่พัลส์นาฬิกาถัดไปจะเริ่ม จากนั้นเราจะได้ช่วงที่แท้จริงของเป้าหมายและเรียกอีกอย่างว่าช่วงสูงสุดที่ไม่ชัดเจนของเป้าหมายหรือเรียกง่ายๆว่าmaximum unambiguous range.

ทดแทน $R=R_{un}$ และ $T=T_P$ ในสมการที่ 1

$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:Equation\:3$$

จากสมการ 2 เราจะได้เวลาการทำซ้ำของพัลส์ $T_P$ ในฐานะที่เป็นส่วนกลับของความถี่การทำซ้ำของพัลส์ $f_P$. Mathematicallyสามารถแสดงเป็น

$$T_P=\frac{1}{f_P}\:\:\:\:\:Equation\:4$$

แทนสมการ 4 ในสมการ 3

$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$

$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:Equation\:5$$

เราสามารถใช้สมการ 3 หรือสมการ 5 สำหรับการคำนวณช่วงสูงสุดที่ไม่คลุมเครือของเป้าหมาย

• เราจะได้รับค่าของช่วงสูงสุดที่ไม่ชัดเจนของเป้าหมาย $R_{un}$ โดยการแทนค่าของ $C$ และ $T_P$ ในสมการ 3.

• ในทำนองเดียวกันเราจะได้รับค่าของช่วงสูงสุดที่ไม่ชัดเจนของเป้าหมาย $R_{un}$ โดยการแทนค่าของ $C$ และ $f_P$ ในสมการ 5.

ช่วงต่ำสุด

เราจะได้รับไฟล์ minimum rangeของเป้าหมายเมื่อเราพิจารณาเวลาที่สัญญาณสะท้อนต้องได้รับที่เรดาร์หลังจากสัญญาณที่ส่งจากเรดาร์เป็นความกว้างของพัลส์ เรียกอีกอย่างว่าระยะที่สั้นที่สุดของเป้าหมาย

ทดแทน $R=R_{min}$ และ $T=\tau$ ในสมการที่ 1

$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:Equation\:6$$

เราจะได้รับค่าของช่วงต่ำสุดของเป้าหมาย $R_{min}$ โดยการแทนค่าของ $C$ และ $\tau$ ในสมการ 6.

สมการช่วงเรดาร์มีประโยชน์ในการทราบช่วงของเป้าหมาย theoretically. ในบทนี้เราจะพูดถึงรูปแบบมาตรฐานของสมการช่วงเรดาร์จากนั้นจะกล่าวถึงสมการช่วงเรดาร์ที่ปรับเปลี่ยนทั้งสองรูปแบบ

เราจะได้รูปแบบของสมการช่วงเรดาร์ที่แก้ไขแล้วจากรูปแบบมาตรฐานของสมการช่วงเรดาร์ ตอนนี้ให้เราพูดคุยเกี่ยวกับที่มาของรูปแบบมาตรฐานของสมการช่วงเรดาร์

ที่มาของสมการช่วงเรดาร์

รูปแบบมาตรฐานของสมการช่วงเรดาร์เรียกอีกอย่างว่ารูปแบบง่ายๆของสมการช่วงเรดาร์ ตอนนี้ให้เราได้รูปแบบมาตรฐานของสมการช่วงเรดาร์

เรารู้ว่า power densityไม่มีอะไรนอกจากอัตราส่วนของกำลังและพื้นที่ ดังนั้นความหนาแน่นของพลังงาน$P_{di}$ ในระยะไกล R จากเรดาร์สามารถแสดงทางคณิตศาสตร์เป็น -

$$P_{di}=\frac{P_t}{4\pi R^2}\:\:\:\:\:Equation\:1$$

ที่ไหน

$P_t$

ความหนาแน่นของกำลังไฟฟ้าข้างต้นใช้ได้สำหรับเสาอากาศแบบไอโซทรอปิก โดยทั่วไป Radars ใช้เสาอากาศแบบกำหนดทิศทาง ดังนั้นความหนาแน่นของพลังงาน$P_{dd}$ เนื่องจากเสาอากาศทิศทางจะเป็น -

$$P_{dd}=\frac{P_tG}{4\pi R^2}\:\:\:\:\:Equation\:2$$

เป้าหมายจะแผ่พลังไปในทิศทางที่แตกต่างจากกำลังไฟฟ้าเข้าที่ได้รับ ปริมาณพลังงานที่สะท้อนกลับไปยังเรดาร์ขึ้นอยู่กับส่วนตัดขวาง ดังนั้นความหนาแน่นของพลังงาน$P_{de}$ ของสัญญาณสะท้อนที่เรดาร์สามารถแสดงทางคณิตศาสตร์เป็น -

$$P_{de}=P_{dd}\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:3$$ แทนสมการ 2 ในสมการ 3

$$P_{de}=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:4$$

จำนวน power, $P_r$ received โดยเรดาร์ขึ้นอยู่กับรูรับแสงที่มีประสิทธิภาพ $A_e$ ของเสาอากาศรับ

$$P_r=P_{de}A_e\:\:\:\:\:Equation\:5$$

แทนสมการ 4 ในสมการ 5

$$P_r=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )A_e$$

$$\Rightarrow P_r=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 R^4}$$

$$\Rightarrow R^4=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}$$

$$\Rightarrow R=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}\right ]^{1/4}\:\:\:\:\:Equation\:6$$

รูปแบบมาตรฐานของสมการช่วงเรดาร์

หากสัญญาณสะท้อนมีพลังงานน้อยกว่ากำลังของสัญญาณที่ตรวจจับได้ต่ำสุดเรดาร์จะไม่สามารถตรวจจับเป้าหมายได้เนื่องจากอยู่เกินขีด จำกัด สูงสุดของช่วงเรดาร์

ดังนั้นเราสามารถพูดได้ว่าช่วงของเป้าหมายเป็นช่วงสูงสุดเมื่อสัญญาณสะท้อนที่ได้รับมีกำลังเท่ากับสัญญาณที่ตรวจจับได้ต่ำสุด เราจะได้สมการต่อไปนี้โดยการแทนที่$R=R_{Max}$ และ $P_r=S_{min}$ ในสมการ 6.

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:7$$

สมการที่ 7 แทนค่า standard formของสมการช่วงเรดาร์ โดยใช้สมการข้างต้นเราสามารถหาช่วงสูงสุดของเป้าหมายได้

รูปแบบที่ปรับเปลี่ยนของสมการช่วงเรดาร์

เราทราบความสัมพันธ์ดังต่อไปนี้ระหว่าง Gain ของเสาอากาศทิศทาง $G$ และรูรับแสงที่มีประสิทธิภาพ $A_e$.

$$G=\frac{4\pi A_e}{\lambda^2}\:\:\:\:\:Equation\:8$$

แทนสมการ 8 ในสมการ 7

$$R_{Max}=\left [ \frac{P_t\sigma A_e}{\left ( 4\pi \right )^2S_{min}}\left ( \frac{4\pi A_e}{\lambda^2} \right ) \right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:9$$

สมการที่ 9 แทนค่า modified formของสมการช่วงเรดาร์ โดยใช้สมการข้างต้นเราสามารถหาช่วงสูงสุดของเป้าหมายได้

เราจะได้รับความสัมพันธ์ดังต่อไปนี้ระหว่างรูรับแสงที่มีประสิทธิภาพ $A_e$ และกำไรของเสาอากาศทิศทาง $G$ จากสมการ 8.

$$A_e=\frac{G\lambda^2}{4\pi}\:\:\:\:\:Equation\:10$$

แทนสมการ 10 ในสมการ 7.

$$R_{Max}=\left [\frac{P_tG\sigma}{\left (4\pi\right )^2 S_{min}}(\frac{G\lambda^2}{4\pi})\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG^2 \lambda^2 \sigma}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:11$$

สมการ 11 แทน another modified form ของสมการช่วงเรดาร์ โดยใช้สมการข้างต้นเราสามารถหาช่วงสูงสุดของเป้าหมายได้

Note - จากข้อมูลที่ระบุเราสามารถค้นหาช่วงสูงสุดของเป้าหมายได้โดยใช้หนึ่งในสามสมการนี้ ได้แก่

• สมการ 7
• สมการ 9
• สมการ 11

ตัวอย่างปัญหา

ในส่วนก่อนหน้านี้เราได้รับรูปแบบมาตรฐานและรูปแบบที่ปรับเปลี่ยนของสมการช่วงเรดาร์ ตอนนี้ให้เราแก้ปัญหาเล็กน้อยโดยใช้สมการเหล่านั้น

ปัญหา 1

คำนวณ maximum range of Radar สำหรับคุณสมบัติดังต่อไปนี้ -

• พลังสูงสุดที่ส่งโดยเรดาร์ $P_t=250KW$
• กำไรของการส่งเสาอากาศ $G=4000$
• รูรับแสงที่มีประสิทธิภาพของเสาอากาศรับ $A_e=4\:m^2$
• เรดาร์ตัดขวางของเป้าหมาย $\sigma=25\:m^2$
• พลังของสัญญาณขั้นต่ำที่ตรวจจับได้ $S_{min}=10^{-12}W$

วิธีการแก้

เราสามารถใช้สิ่งต่อไปนี้ standard form ของสมการช่วงเรดาร์เพื่อคำนวณช่วงสูงสุดของเรดาร์สำหรับข้อมูลจำเพาะที่กำหนด

$$R_{Max}=\left [\frac{P_tG \sigma A_e}{\left (4\pi \right )^2 S_{min}}\right ]^{1/4}$$

Substitute พารามิเตอร์ที่กำหนดทั้งหมดในสมการข้างต้น

$$R_{Max}=\left [\frac{ \left ( 250\times 10^3 \right )\left ( 4000 \right )\left ( 25 \right )\left ( 4 \right )}{\left ( 4\pi \right )^2 \left ( 10^{-12} \right )} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=158\:KM$$

ดังนั้นไฟล์ maximum range of Radar สำหรับคุณสมบัติที่กำหนดคือ $158\:KM$.

ปัญหา 2

คำนวณ maximum range of Radar สำหรับคุณสมบัติดังต่อไปนี้

• ความถี่ในการทำงาน $f=10GHZ$
• พลังสูงสุดที่ส่งโดยเรดาร์ $P_t=400KW$
• รูรับแสงที่มีประสิทธิภาพของเสาอากาศรับ $A_e=5\:m^2$
• เรดาร์ตัดขวางของเป้าหมาย $\sigma=30\:m^2$
• พลังของสัญญาณขั้นต่ำที่ตรวจจับได้ $S_{min}=10^{-10}W$

วิธีการแก้

เรารู้สูตรต่อไปนี้สำหรับ operating wavelength, $\lambda$ ในแง่ของความถี่ในการทำงาน f.

$$\lambda =\frac{C}{f}$$

ทดแทน $C=3\times 10^8m/sec$ และ $f=10GHZ$ ในสมการข้างต้น

$$\lambda =\frac{3\times 10^8}{10\times 10^9}$$

$$\Rightarrow \lambda=0.03m$$

ดังนั้น operating wavelength,$\lambda$ เท่ากับ $0.03m$เมื่อความถี่ในการทำงาน $f$ คือ $10GHZ$.

เราสามารถใช้สิ่งต่อไปนี้ modified form ของสมการช่วงเรดาร์เพื่อคำนวณช่วงสูงสุดของเรดาร์สำหรับข้อมูลจำเพาะที่กำหนด

$$R_{Max}=\left [\frac{P_t \sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}$$

Substituteพารามิเตอร์ที่กำหนดในสมการด้านบน

$$R_{Max}=\left [ \frac{\left ( 400\times 10^3 \right )\left ( 30 \right )\left ( 5^2 \right )}{4\pi\left ( 0.003 \right )^2\left ( 10 \right )^{-10}} \right ]^{1/4}$$

$$\Rightarrow R_{Max}=128KM$$

ดังนั้นไฟล์ maximum range of Radar สำหรับคุณสมบัติที่กำหนดคือ $128\:KM$.

ปัจจัยที่มีผลต่อประสิทธิภาพของเรดาร์เรียกว่าปัจจัยด้านประสิทธิภาพของเรดาร์ ในบทนี้ให้เราพิจารณาเกี่ยวกับปัจจัยเหล่านั้น เรารู้ว่าต่อไปนี้standard form ของสมการช่วงเรดาร์ซึ่งมีประโยชน์สำหรับการคำนวณช่วงสูงสุดของเรดาร์สำหรับข้อมูลจำเพาะที่กำหนด

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

ที่ไหน

$P_t$ คือกำลังสูงสุดที่ส่งโดยเรดาร์

$G$ คือกำไรของการส่งเสาอากาศ

$\sigma$ คือหน้าตัดของเรดาร์ของเป้าหมาย

$A_e$ คือรูรับแสงที่มีประสิทธิภาพของเสาอากาศรับสัญญาณ

$S_{min}$ คือพลังของสัญญาณขั้นต่ำที่ตรวจจับได้

จากสมการข้างต้นเราสามารถสรุปได้ดังต่อไปนี้ conditions ควรได้รับการพิจารณาเพื่อให้ได้ระยะของเรดาร์สูงสุด

• พลังสูงสุดที่ส่งโดยเรดาร์ $P_t$ ควรจะสูง
• กำไรของเสาอากาศส่ง $G$ ควรจะสูง
• เรดาร์ตัดขวางของเป้าหมาย $\sigma$ ควรจะสูง
• รูรับแสงที่มีประสิทธิภาพของเสาอากาศรับ $A_e$ ควรจะสูง
• พลังของสัญญาณขั้นต่ำที่ตรวจจับได้ $S_{min}$ ควรต่ำ

เป็นการยากที่จะทำนายช่วงของเป้าหมายจากรูปแบบมาตรฐานของสมการช่วงเรดาร์ ซึ่งหมายความว่าระดับความแม่นยำที่กำหนดโดยสมการช่วงเรดาร์เกี่ยวกับช่วงของเป้าหมายนั้นน้อยกว่า เนื่องจากพารามิเตอร์เช่น Radar cross section ของเป้าหมาย$\sigma$ และสัญญาณขั้นต่ำที่ตรวจจับได้ $S_{min}$ คือ statistical in nature.

สัญญาณขั้นต่ำที่ตรวจจับได้

หากสัญญาณสะท้อนมีกำลังไฟต่ำสุดการตรวจจับสัญญาณนั้นโดยเรดาร์เรียกว่า minimum detectable signal. ซึ่งหมายความว่าเรดาร์ไม่สามารถตรวจจับสัญญาณสะท้อนได้หากสัญญาณนั้นมีพลังงานน้อยกว่ากำลังไฟฟ้าขั้นต่ำ

โดยทั่วไปแล้ว Radar จะรับสัญญาณสะท้อนพร้อมกับสัญญาณรบกวน หากใช้ค่าขีด จำกัด สำหรับการตรวจจับการมีอยู่ของเป้าหมายจากสัญญาณที่ได้รับการตรวจจับนั้นจะเรียกว่าthreshold detection.

เราต้องเลือกค่าเกณฑ์ที่เหมาะสมตามความแรงของสัญญาณที่ตรวจพบ

• ควรเลือกค่าขีด จำกัด ที่สูงเมื่อความแรงของสัญญาณที่ตรวจพบสูงเพื่อที่จะกำจัดสัญญาณรบกวนที่ไม่ต้องการที่มีอยู่ในนั้น

• ในทำนองเดียวกันควรเลือกค่าขีด จำกัด ต่ำเมื่อความแรงของสัญญาณที่ตรวจพบต่ำ

ดังต่อไปนี้ figure แสดงให้เห็นถึงแนวคิดนี้ -

ก typical waveformของเครื่องรับเรดาร์แสดงในรูปด้านบน แกน x และแกน y แทนเวลาและแรงดันไฟฟ้าตามลำดับ ค่า rms ของสัญญาณรบกวนและค่าเกณฑ์ถูกระบุด้วยเส้นประในรูปด้านบน

เราได้พิจารณาสามจุดคือ A, B & C ในรูปด้านบนเพื่อระบุการตรวจจับที่ถูกต้องและการตรวจจับที่ขาดหายไป

• ค่าของสัญญาณที่จุด A มากกว่าค่าเกณฑ์ ดังนั้นจึงเป็นvalid detection.

• ค่าของสัญญาณที่จุด B เท่ากับค่าเกณฑ์ ดังนั้นจึงเป็นvalid detection.

• แม้ว่าค่าของสัญญาณที่จุด C จะใกล้เคียงกับค่า threshold แต่ก็เป็นค่า missing detection. เนื่องจากค่าของสัญญาณที่จุด C น้อยกว่าค่าเกณฑ์

ดังนั้นคะแนน A & B คือการตรวจจับที่ถูกต้อง ในขณะที่จุด C คือการตรวจจับที่หายไป

ตัวรับสัญญาณรบกวน

หากเครื่องรับสร้างส่วนประกอบสัญญาณรบกวนเข้าไปในสัญญาณซึ่งได้รับที่เครื่องรับสัญญาณรบกวนชนิดนั้นจะเรียกว่าสัญญาณรบกวนของเครื่องรับ receiver noiseเป็นส่วนประกอบที่ไม่ต้องการ เราควรพยายามกำจัดมันด้วยความระมัดระวัง

อย่างไรก็ตามมีเสียงรบกวนชนิดหนึ่งที่เรียกว่าสัญญาณรบกวนจากความร้อน เกิดขึ้นเนื่องจากการเคลื่อนที่เชิงความร้อนของอิเล็กตรอนในการนำกระแสไฟฟ้า ในทางคณิตศาสตร์เราสามารถเขียนได้thermal noise power, $N_i$ ผลิตที่เครื่องรับเป็น -

$$N_i=KT_oB_n$$

ที่ไหน

$K$ คือค่าคงที่ของ Boltzmann และเท่ากับ $1.38\times 10^{-23}J/deg$

$T_o$ คืออุณหภูมิสัมบูรณ์และเท่ากับ $290^0K$

$B_n$ คือความกว้างของแถบรับ

ร่างของบุญ

Figure of Merit, F คืออะไรนอกจากอัตราส่วนของอินพุต SNR, $(SNR)_i$ และเอาต์พุต SNR $(SNR)_o$. ในทางคณิตศาสตร์สามารถแสดงเป็น -

$$F=\frac{(SNR)_i}{(SNR)_o}$$

$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$

$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$

$$\Rightarrow S_i=\frac{FN_iS_o}{N_o}$$

ทดแทน $N_i=KT_oB_n$ ในสมการข้างต้น

$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$

กำลังสัญญาณอินพุตจะมีค่าต่ำสุดเมื่อเอาต์พุต SNR มีค่าต่ำสุด

$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$

แทนข้างต้น $S_{min}$ ในรูปแบบมาตรฐานของสมการช่วงเรดาร์ต่อไปนี้

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}}\right ]^{1/4}$$

จากสมการข้างต้นเราสามารถสรุปได้ดังต่อไปนี้ conditions ควรได้รับการพิจารณาเพื่อให้ได้ระยะของเรดาร์สูงสุด

• พลังสูงสุดที่ส่งโดยเรดาร์ $P_t$ ควรจะสูง
• กำไรของเสาอากาศส่ง $G$ ควรจะสูง
• เรดาร์ตัดขวางของเป้าหมาย $\sigma$ ควรจะสูง
• รูรับแสงที่มีประสิทธิภาพของเสาอากาศรับ $A_e$ ควรจะสูง
• รูปของ Merit F ควรอยู่ในระดับต่ำ
• แบนด์วิดท์ตัวรับ $B_n$ ควรต่ำ

ในบทนี้เราจะพูดถึงเรดาร์ประเภทต่างๆโดยสังเขป บทนี้ให้ข้อมูลสั้น ๆ เกี่ยวกับประเภทของเรดาร์ เรดาร์สามารถแบ่งออกเป็นดังต่อไปนี้two types ขึ้นอยู่กับประเภทของสัญญาณที่เรดาร์สามารถใช้งานได้

• เรดาร์พัลส์
• เรดาร์คลื่นต่อเนื่อง

ตอนนี้ให้เราพูดคุยเกี่ยวกับ Radars ทั้งสองประเภทนี้ทีละประเภท

เรดาร์พัลส์

เรดาร์ซึ่งทำงานด้วยสัญญาณพัลส์เรียกว่า Pulse Radar. Pulse Radars สามารถแบ่งออกเป็นสองประเภทดังต่อไปนี้ตามประเภทของเป้าหมายที่ตรวจพบ

• Pulse Radar พื้นฐาน
• การเคลื่อนย้ายเรดาร์บ่งชี้เป้าหมาย

ตอนนี้ให้เราหารือเกี่ยวกับเรดาร์ทั้งสองสั้น ๆ

Pulse Radar พื้นฐาน

เรดาร์ซึ่งทำงานด้วยสัญญาณพัลส์สำหรับตรวจจับเป้าหมายที่อยู่นิ่งเรียกว่า Basic Pulse Radarหรือเรียกง่ายๆว่า Pulse Radar ใช้เสาอากาศเดียวสำหรับทั้งการส่งและรับสัญญาณด้วยความช่วยเหลือของ Duplexer

เสาอากาศจะส่งสัญญาณพัลส์ทุกพัลส์นาฬิกา ควรเลือกระยะเวลาระหว่างพัลส์นาฬิกาทั้งสองในลักษณะที่ควรรับสัญญาณสะท้อนที่สอดคล้องกับพัลส์นาฬิกาปัจจุบันก่อนพัลส์นาฬิกาถัดไป

การเคลื่อนย้ายเรดาร์บ่งชี้เป้าหมาย

เรดาร์ซึ่งทำงานด้วยสัญญาณพัลส์สำหรับตรวจจับเป้าหมายที่ไม่อยู่นิ่งเรียกว่า Moving Target Indication Radar หรือเรียกง่ายๆว่า MTI Radar. ใช้เสาอากาศเดียวสำหรับทั้งการส่งและรับสัญญาณด้วยความช่วยเหลือของ Duplexer

MTI Radar ใช้หลักการของ Doppler effect สำหรับการแยกแยะเป้าหมายที่ไม่อยู่นิ่งจากวัตถุที่อยู่นิ่ง

เรดาร์คลื่นต่อเนื่อง

เรียกว่าเรดาร์ซึ่งทำงานด้วยสัญญาณหรือคลื่นต่อเนื่องเรียกว่า Continuous Wave Radar. พวกเขาใช้ Doppler Effect ในการตรวจจับเป้าหมายที่ไม่อยู่นิ่ง เรดาร์คลื่นต่อเนื่องสามารถแบ่งออกเป็นสองประเภทดังต่อไปนี้

• เรดาร์คลื่นต่อเนื่องที่ไม่มีการปรับเปลี่ยน
• เรดาร์คลื่นต่อเนื่องที่ปรับความถี่

ตอนนี้ให้เราพูดคุยเกี่ยวกับเรดาร์ทั้งสองสั้น ๆ

เรดาร์คลื่นต่อเนื่องที่ไม่มีการปรับเปลี่ยน

เรดาร์ซึ่งทำงานด้วยสัญญาณต่อเนื่อง (คลื่น) สำหรับตรวจจับเป้าหมายที่ไม่อยู่นิ่งเรียกว่า Unmodulated Continuous Wave Radar หรือเรียกง่ายๆว่า CW Radar. เรียกอีกอย่างว่า CW Doppler Radar

เรดาร์นี้ต้องใช้เสาอากาศสองอัน ในสองเสาอากาศนี้เสาอากาศหนึ่งตัวใช้สำหรับส่งสัญญาณและอีกเสาอากาศใช้สำหรับรับสัญญาณ วัดความเร็วของเป้าหมายเท่านั้น แต่ไม่วัดระยะของเป้าหมายจากเรดาร์

เรดาร์คลื่นต่อเนื่องที่ปรับความถี่

ถ้า CW Doppler Radar ใช้การมอดูเลตความถี่เรดาร์นั้นจะเรียกว่าคลื่นความถี่ต่อเนื่องมอดูเลต (FMCW)เรดาร์หรือ FMCW Doppler Radar เรียกอีกอย่างว่า Continuous Wave Frequency Modulated Radar หรือ CWFM Radar

เรดาร์นี้ต้องใช้เสาอากาศสองอัน ในนั้นเสาอากาศหนึ่งตัวใช้สำหรับส่งสัญญาณและเสาอากาศอื่นใช้สำหรับรับสัญญาณ ไม่เพียง แต่วัดความเร็วของเป้าหมายเท่านั้น แต่ยังวัดระยะห่างของเป้าหมายจากเรดาร์ด้วย

ในบทต่อ ๆ ไปเราจะพูดถึงการดำเนินการของ Radars ทั้งหมดนี้โดยละเอียด

เรดาร์ซึ่งทำงานด้วยสัญญาณพัลส์สำหรับตรวจจับเป้าหมายที่อยู่นิ่งเรียกว่า Basic Pulse Radar หรือเรียกง่ายๆว่า Pulse Radar. ในบทนี้ให้เราพิจารณาการทำงานของ Pulse Radar

แผนภาพบล็อกของ Pulse Radar

Pulse Radar ใช้เสาอากาศเดียวสำหรับทั้งการส่งและรับสัญญาณด้วยความช่วยเหลือของ Duplexer ต่อไปนี้คือไฟล์block diagram ของ Pulse Radar -

ให้เราดูไฟล์ function ของ Pulse Radar แต่ละบล็อก -

• Pulse Modulator - สร้างสัญญาณพัลส์มอดูเลตและใช้กับเครื่องส่งสัญญาณ

• Transmitter - ส่งสัญญาณพัลส์มอดูเลตซึ่งเป็นรถไฟของพัลส์ซ้ำ ๆ

• Duplexer- เป็นสวิตช์ไมโครเวฟซึ่งเชื่อมต่อเสาอากาศกับทั้งส่วนเครื่องส่งและส่วนรับสลับกัน เสาอากาศส่งสัญญาณพัลส์มอดูเลตเมื่อตัวพลิกหน้าเชื่อมต่อเสาอากาศเข้ากับเครื่องส่งสัญญาณ ในทำนองเดียวกันสัญญาณที่เสาอากาศได้รับจะถูกส่งไปยังเครื่องขยายสัญญาณ RF เสียงรบกวนต่ำเมื่อตัวพลิกหน้าเชื่อมต่อเสาอากาศกับเครื่องขยายสัญญาณ RF เสียงรบกวนต่ำ

• Low Noise RF Amplifier- ขยายสัญญาณ RF ที่อ่อนแอซึ่งได้รับจากเสาอากาศ เอาต์พุตของเครื่องขยายเสียงนี้เชื่อมต่อกับมิกเซอร์

• Local Oscillator- สร้างสัญญาณที่มีความถี่คงที่ เอาต์พุตของ Local Oscillator เชื่อมต่อกับ Mixer

• Mixer- เรารู้ว่ามิกเซอร์สามารถสร้างทั้งผลรวมและความแตกต่างของความถี่ที่ใช้กับมัน ซึ่งความแตกต่างของความถี่จะเป็นประเภท Intermediate Frequency (IF)

• IF Amplifier- เครื่องขยายเสียง IF ขยายสัญญาณความถี่กลาง (IF) เครื่องขยายเสียง IF ที่แสดงในรูปอนุญาตเฉพาะความถี่กลางซึ่งได้รับจากมิกเซอร์และขยายสัญญาณ ปรับปรุงอัตราส่วนสัญญาณต่อเสียงรบกวนที่เอาต์พุต

• Detector - มัน demodulate สัญญาณซึ่งได้มาจากเอาท์พุทของ IF Amplifier

• Video Amplifier - ตามชื่อที่แนะนำมันจะขยายสัญญาณวิดีโอซึ่งได้มาจากเอาต์พุตของเครื่องตรวจจับ

• Display - โดยทั่วไปจะแสดงสัญญาณวิดีโอที่ขยายบนหน้าจอ CRT

ในบทนี้เราจะพูดถึงวิธีการทำงานของ Pulse Radar และมีประโยชน์อย่างไรสำหรับการตรวจจับเป้าหมายที่อยู่นิ่ง ในบทต่อ ๆ ไปเราจะพูดถึง Radars ซึ่งมีประโยชน์สำหรับการตรวจจับเป้าหมายที่ไม่อยู่นิ่ง

ในบทนี้เราจะเรียนรู้เกี่ยวกับ Doppler Effect ในระบบเรดาร์

หากเป้าหมายไม่อยู่นิ่งจะมีการเปลี่ยนแปลงในความถี่ของสัญญาณที่ส่งจากเรดาร์และที่ได้รับจากเรดาร์ ผลกระทบนี้เรียกว่าDoppler effect.

ตามเอฟเฟกต์ Doppler เราจะได้รับสองกรณีที่เป็นไปได้ดังต่อไปนี้ -

• frequency ของสัญญาณที่ได้รับจะ increaseเมื่อเป้าหมายเคลื่อนที่ไปยังทิศทางของเรดาร์

• frequency ของสัญญาณที่ได้รับจะ decreaseเมื่อเป้าหมายเคลื่อนที่ออกจากเรดาร์

ตอนนี้ให้เราหาสูตรสำหรับความถี่ Doppler

การมาของความถี่ Doppler

ระยะห่างระหว่างเรดาร์และเป้าหมายไม่มีอะไรนอกจาก Range ของเป้าหมายหรือเพียงแค่ช่วง R ดังนั้นระยะทางทั้งหมดระหว่างเรดาร์และเป้าหมายในเส้นทางการสื่อสารสองทางจะเป็น 2R เนื่องจากเรดาร์ส่งสัญญาณไปยังเป้าหมายและเป้าหมายจึงส่งสัญญาณสะท้อนไปยังเรดาร์

ถ้า $\lambda$ คือความยาวคลื่นหนึ่งความยาวคลื่น N ที่มีอยู่ในเส้นทางการสื่อสารสองทางระหว่างเรดาร์และเป้าหมายจะเท่ากับ $2R/\lambda$.

เรารู้ว่าความยาวคลื่นหนึ่ง $\lambda$ สอดคล้องกับการเดินทางเชิงมุมของ $2\pi$เรเดียน ดังนั้นtotal angle of excursion ทำโดยคลื่นแม่เหล็กไฟฟ้าในระหว่างเส้นทางการสื่อสารสองทางระหว่างเรดาร์และเป้าหมายจะเท่ากับ $4\pi R/\lambda$ เรเดียน

ต่อไปนี้เป็นสูตรทางคณิตศาสตร์สำหรับ angular frequency, $\omega$ -

$$\omega=2\pi f\:\:\:\:\:Equation\:1$$

สมการต่อไปนี้แสดงความสัมพันธ์ทางคณิตศาสตร์ระหว่างความถี่เชิงมุม $\omega$ และมุมเฟส $\phi$ -

$$\omega=\frac{d\phi }{dt}\:\:\:\:\:Equation\:2$$

Equate เงื่อนไขด้านขวามือของสมการ 1 และสมการ 2 เนื่องจากเงื่อนไขด้านซ้ายมือของทั้งสองสมการนั้นเหมือนกัน

$$2\pi f=\frac{d\phi }{dt}$$

$$\Rightarrow f =\frac{1}{2\pi}\frac{d\phi }{dt}\:\:\:\:\:Equation\:3$$

Substitute,$f=f_d$ และ $\phi=4\pi R/\lambda$ ในสมการ 3.

$$f_d =\frac{1}{2\pi}\frac{d}{dt}\left ( \frac{4\pi R}{\lambda} \right )$$

$$\Rightarrow f_d =\frac{1}{2\pi}\frac{4\pi}{\lambda}\frac{dR}{dt}$$

$$\Rightarrow f_d =\frac{2V_r}{\lambda}\:\:\:\:\:Equation\:4$$

ที่ไหน

$f_d$ คือความถี่ Doppler

$V_r$ คือความเร็วสัมพัทธ์

เราสามารถหาค่าของความถี่ Doppler $f_d$ โดยการแทนค่าของ $V_r$ และ $\lambda$ ในสมการ 4.

Substitute, $\lambda=C/f$ ในสมการ 4.

$$f_d =\frac{2V_r}{C/f}$$

$$\Rightarrow f_d =\frac{2V_rf}{C}\:\:\:\:\:Equation\:5$$

ที่ไหน

$f$ คือความถี่ของสัญญาณที่ส่ง

$C$ คือความเร็วแสงและเท่ากับ $3\times 10^8m/sec$

เราสามารถหาค่าความถี่ Doppler $f_d$ โดยการแทนค่าของ $V_r,f$ และ $C$ ในสมการ 5.

Note - ทั้งสมการ 4 และสมการ 5 แสดงสูตรของความถี่ดอปเลอร์ $f_d$. เราสามารถใช้สมการ 4 หรือสมการ 5 ในการค้นหาDoppler frequency, $f_d$ ตามข้อมูลที่กำหนด

ตัวอย่างปัญหา

หากเรดาร์ทำงานที่ความถี่ $5GHZ$จากนั้นค้นหาไฟล์ Doppler frequency ของเครื่องบินที่เคลื่อนที่ด้วยความเร็ว 100 กิโลเมตรต่อชั่วโมง

วิธีการแก้

ให้

ความถี่ของสัญญาณที่ส่ง $f=5GHZ$

ความเร็วของเครื่องบิน (เป้าหมาย) $V_r=100KMph$

$$\Rightarrow V_r=\frac{100\times 10^3}{3600}m/sec$$

$$\Rightarrow V_r=27.78m/sec$$

เราได้แปลงความเร็วของเครื่องบินที่กำหนด (เป้าหมาย) ซึ่งมีอยู่ใน KMph เป็น m / วินาทีที่เทียบเท่า

เรารู้ว่าความเร็วของแสง $C=3\times 10^8m/sec$

ต่อไปนี้คือไฟล์ formula for Doppler frequency -

$$f_d=\frac{2Vrf}{C}$$

Substitute ค่าของð ?? '‰ð ??' Ÿ, $V_r,f$ และ $C$ ในสมการข้างต้น

$$\Rightarrow f_d=\frac{2\left ( 27.78 \right )\left ( 5\times 10^9 \right )}{3\times 10^8}$$

$$\Rightarrow f_d=926HZ$$

ดังนั้นค่าของ Doppler frequency, $f_d$ คือ $926HZ$ สำหรับข้อกำหนดที่กำหนด

เรดาร์พื้นฐานใช้เสาอากาศเดียวกันสำหรับทั้งการส่งและรับสัญญาณ เราสามารถใช้เรดาร์ประเภทนี้ได้เมื่อเป้าหมายอยู่นิ่งกล่าวคือไม่เคลื่อนที่และ / หรือเมื่อเรดาร์นั้นสามารถสั่งงานด้วยสัญญาณพัลส์

Radar ซึ่งทำงานด้วยสัญญาณต่อเนื่อง (คลื่น) สำหรับตรวจจับเป้าหมายที่ไม่อยู่นิ่งเรียกว่า Continuous Wave Radar หรือเรียกง่ายๆ CW Radar. เรดาร์นี้ต้องใช้เสาอากาศสองอัน ในนั้นเสาอากาศหนึ่งตัวใช้สำหรับส่งสัญญาณและเสาอากาศอื่นใช้สำหรับรับสัญญาณ

แผนภาพบล็อกของ CW Radar

เรารู้ว่า CW Doppler Radar มีเสาอากาศสองตัว - ส่งเสาอากาศและเสาอากาศรับ รูปต่อไปนี้แสดงไฟล์block diagram ของ CW Radar -

แผนภาพบล็อกของ CW Doppler Radar ประกอบด้วยชุดบล็อกและ function ของแต่ละบล็อกจะกล่าวถึงด้านล่าง

• CW Transmitter - สร้างสัญญาณแอนะล็อกที่มีความถี่ $f_o$. เอาต์พุตของ CW Transmitter เชื่อมต่อกับทั้งเสาอากาศส่งและมิกเซอร์ -I

• Local Oscillator - สร้างสัญญาณที่มีความถี่ $f_l$. เอาต์พุตของ Local Oscillator เชื่อมต่อกับ Mixer-I

• Mixer-I- มิกเซอร์สามารถสร้างทั้งผลรวมและความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่ของ$f_o$ และ $f_l$ถูกนำไปใช้กับ Mixer-I ดังนั้น Mixer-I จะสร้างเอาต์พุตที่มีความถี่$f_o+f_l$ หรือ $f_o−f_l$.

• Side Band Filter- ตามชื่อที่แนะนำตัวกรองแถบด้านข้างอนุญาตให้ใช้ความถี่แถบด้านข้างโดยเฉพาะไม่ว่าจะเป็นความถี่แถบด้านบนหรือความถี่แถบด้านล่าง ตัวกรองแถบด้านข้างที่แสดงในรูปด้านบนจะสร้างความถี่แถบด้านบนเท่านั้นกล่าวคือ$f_o+f_l$.

• Mixer-II- มิกเซอร์สามารถสร้างทั้งผลรวมและความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่ของ$f_o+f_l$ และ $f_o\pm f_d$ถูกนำไปใช้กับ Mixer-II ดังนั้น Mixer-II จะสร้างเอาต์พุตที่มีความถี่เป็น 2$f_o+f_l\pm f_d$ หรือ $f_l\pm f_d$.

• IF Amplifier- เครื่องขยายเสียง IF ขยายสัญญาณความถี่กลาง (IF) เครื่องขยายเสียง IF ที่แสดงในรูปอนุญาตเฉพาะความถี่กลาง$f_l\pm f_d$ และขยายมัน

• Detector - ตรวจจับสัญญาณซึ่งมีความถี่ Doppler $f_d$.

• Doppler Amplifier - ตามชื่อที่แนะนำเครื่องขยายเสียง Doppler จะขยายสัญญาณซึ่งมีความถี่ Doppler $f_d$.

• Indicator - ระบุข้อมูลที่เกี่ยวข้องกับความเร็วสัมพัทธ์และเป้าหมายว่าเป็นขาเข้าหรือขาออก

CW Doppler Radars ให้การวัดที่แม่นยำของ relative velocities. ดังนั้นจึงใช้สิ่งเหล่านี้เป็นส่วนใหญ่ซึ่งข้อมูลของความเร็วมีความสำคัญมากกว่าช่วงจริง

ถ้า CW Doppler Radar ใช้การมอดูเลตความถี่เรดาร์นั้นจะเรียกว่า FMCW Doppler Radar หรือเพียงแค่ FMCW Radar. เรียกอีกอย่างว่า Continuous Wave Frequency Modulated Radar หรือ CWFM Radar ไม่เพียง แต่วัดความเร็วของเป้าหมายเท่านั้น แต่ยังวัดระยะห่างของเป้าหมายจากเรดาร์ด้วย

แผนภาพบล็อกของเรดาร์ FMCW

FMCW Radar ส่วนใหญ่จะใช้เป็น Radar Altimeter เพื่อวัดความสูงที่แน่นอนขณะลงจอดเครื่องบิน รูปต่อไปนี้แสดงไฟล์block diagram ของ FMCW Radar -

FMCW Radarประกอบด้วยเสาอากาศสองตัว - ส่งเสาอากาศและเสาอากาศรับดังแสดงในรูป เสาอากาศส่งสัญญาณจะส่งสัญญาณและเสาอากาศรับสัญญาณจะรับสัญญาณสะท้อน

แผนภาพบล็อกของเรดาร์ FMCW มีลักษณะคล้ายกับแผนภาพบล็อกของ CW Radar ประกอบด้วยบล็อกที่แก้ไขเล็กน้อยและบล็อกอื่น ๆ นอกเหนือจากบล็อกที่มีอยู่ในแผนภาพบล็อกของ CW Radar function ของแต่ละบล็อกของ FMCW Radar มีการระบุไว้ด้านล่าง

• FM Modulator - สร้างสัญญาณ Frequency Modulated (FM) ที่มีความถี่ตัวแปร $f_o\left (t \right )$ และใช้กับเครื่องส่ง FM

• FM Transmitter- ส่งสัญญาณ FM ด้วยความช่วยเหลือของการส่งเสาอากาศ เอาต์พุตของ FM Transmitter ยังเชื่อมต่อกับ Mixer-I

• Local Oscillator- โดยทั่วไป Local Oscillator ใช้ในการสร้างสัญญาณ RF แต่ที่นี่มันถูกใช้เพื่อสร้างสัญญาณที่มีความถี่กลาง$f_{IF}$. เอาต์พุตของ Local Oscillator เชื่อมต่อกับทั้ง Mixer-I และ Balanced Detector

• Mixer-I- มิกเซอร์สามารถสร้างทั้งผลรวมและความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่ของ$f_o\left (t \right )$ และ $f_{IF}$ถูกนำไปใช้กับ Mixer-I ดังนั้น Mixer-I จะสร้างเอาต์พุตที่มีความถี่เช่นกัน$f_o\left (t \right )+f_{IF}$ หรือ $f_o\left (t \right )-f_{IF}$.

• Side Band Filter- อนุญาตให้ใช้ความถี่แถบด้านข้างเพียงด้านเดียวเช่นความถี่แถบด้านบนหรือความถี่ด้านล่าง ตัวกรองแถบด้านข้างที่แสดงในรูปจะสร้างความถี่แถบด้านข้างที่ต่ำกว่าเท่านั้น กล่าวคือ$f_o\left (t \right )-f_{IF}$.

• Mixer-II- มิกเซอร์สามารถสร้างทั้งผลรวมและความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่ของ$f_o\left (t \right )-f_{IF}$ และ $f_o\left (t-T \right )$ถูกนำไปใช้กับ Mixer-II ดังนั้น Mixer-II จะสร้างเอาต์พุตที่มีความถี่เช่นกัน$f_o\left (t-T \right )+f_o\left (t \right )-f_{IF}$ หรือ $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$.

• IF Amplifier- เครื่องขยายเสียง IF ขยายสัญญาณความถี่กลาง (IF) เครื่องขยายเสียง IF ที่แสดงในรูปจะขยายสัญญาณที่มีความถี่$f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$. สัญญาณขยายนี้ใช้เป็นอินพุตไปยังเครื่องตรวจจับสมดุล

• Balanced Detector - ใช้ในการผลิตสัญญาณเอาต์พุตที่มีความถี่ $f_o\left (t-T \right )-f_o\left (t \right )$ จากสัญญาณอินพุตสองสัญญาณที่ใช้ซึ่งมีความถี่ของ $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ และ $f_{IF}$. เอาต์พุตของเครื่องตรวจจับสมดุลถูกนำไปใช้เป็นอินพุตไปยังเครื่องขยายความถี่ต่ำ

• Low Frequency Amplifier- ขยายเอาต์พุตของเครื่องตรวจจับสมดุลไปยังระดับที่ต้องการ เอาต์พุตของแอมพลิฟายเออร์ความถี่ต่ำจะใช้กับตัวนับความถี่แบบสวิตช์และตัวนับความถี่เฉลี่ย

• Switched Frequency Counter - มีประโยชน์ในการรับค่าความเร็วดอปเลอร์

• Average Frequency Counter - มีประโยชน์ในการรับค่าของ Range

หากใช้เรดาร์เพื่อตรวจจับเป้าหมายที่เคลื่อนที่ได้เรดาร์ควรได้รับสัญญาณสะท้อนเท่านั้นเนื่องจากเป้าหมายที่เคลื่อนที่ได้นั้น สัญญาณสะท้อนนี้เป็นสัญญาณที่ต้องการ อย่างไรก็ตามในการใช้งานจริง Radar จะรับสัญญาณสะท้อนเนื่องจากวัตถุที่อยู่นิ่งนอกเหนือจากสัญญาณสะท้อนเนื่องจากเป้าหมายที่เคลื่อนที่ได้นั้น

เรียกสัญญาณสะท้อนเนื่องจากวัตถุที่อยู่นิ่ง (สถานที่) เช่นบกและทะเล cluttersเนื่องจากสิ่งเหล่านี้เป็นสัญญาณที่ไม่ต้องการ ดังนั้นเราจึงต้องเลือกเรดาร์ในลักษณะที่พิจารณาเฉพาะสัญญาณสะท้อนเนื่องจากเป้าหมายที่เคลื่อนที่ได้ แต่ไม่ใช่คลัตช์

เพื่อจุดประสงค์นี้ Radar ใช้หลักการของ Doppler Effect ในการแยกแยะเป้าหมายที่ไม่อยู่นิ่งจากวัตถุที่อยู่นิ่ง เรดาร์ประเภทนี้เรียกว่า Moving Target Indicator Radar หรือเรียกง่ายๆว่าMTI Radar.

ตาม Doppler effectความถี่ของสัญญาณที่ได้รับจะเพิ่มขึ้นหากเป้าหมายเคลื่อนที่ไปยังทิศทางของเรดาร์ ในทำนองเดียวกันความถี่ของสัญญาณที่ได้รับจะลดลงหากเป้าหมายกำลังเคลื่อนที่ออกจากเรดาร์

ประเภทของ MTI Radars

เราสามารถแบ่งประเภทของเรดาร์ MTI ได้ดังต่อไปนี้ two types ขึ้นอยู่กับประเภทของเครื่องส่งสัญญาณที่ใช้

• MTI Radar พร้อมเครื่องส่งสัญญาณเพาเวอร์แอมป์
• MTI Radar พร้อมเครื่องส่งสัญญาณ Power Oscillator

ตอนนี้ให้เราพูดคุยเกี่ยวกับ MTI Radars ทั้งสองนี้ทีละรายการ

MTI Radar พร้อมเครื่องส่งสัญญาณเพาเวอร์แอมป์

MTI Radar ใช้เสาอากาศเดียวสำหรับทั้งการส่งและรับสัญญาณด้วยความช่วยเหลือของ Duplexer block diagram ของ MTI Radar พร้อมเครื่องส่งกำลังขยายแสดงดังรูปต่อไปนี้

function ของแต่ละบล็อกของ MTI Radar พร้อมเครื่องส่งสัญญาณกำลังขยายมีการระบุไว้ด้านล่าง

• Pulse Modulator - สร้างสัญญาณพัลส์มอดูเลตและใช้กับเพาเวอร์แอมป์

• Power Amplifier - ขยายระดับพลังงานของสัญญาณพัลส์มอดูเลต

• Local Oscillator - สร้างสัญญาณที่มีความถี่คงที่ $f_l$. ดังนั้นจึงเรียกอีกอย่างว่า Local Oscillator ที่เสถียร เอาต์พุตของ Local Oscillator ถูกนำไปใช้กับทั้ง Mixer-I และ Mixer-II

• Coherent Oscillator - สร้างสัญญาณที่มีความถี่กลาง $f_c$. สัญญาณนี้ใช้เป็นสัญญาณอ้างอิง เอาต์พุตของ Coherent Oscillator ใช้กับทั้ง Mixer-I และ Phase Detector

• Mixer-I- มิกเซอร์สามารถสร้างผลรวมหรือความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่ของ$f_l$ และ $f_c$ถูกนำไปใช้กับ Mixer-I ในที่นี้มิกเซอร์ -I ใช้สำหรับผลิตเอาต์พุตซึ่งมีความถี่$f_l+f_c$.

• Duplexer- เป็นสวิตช์ไมโครเวฟซึ่งเชื่อมต่อเสาอากาศเข้ากับส่วนเครื่องส่งหรือส่วนรับตามข้อกำหนด เสาอากาศส่งสัญญาณที่มีความถี่$f_l+f_c$เมื่อตัวพลิกหน้าเชื่อมต่อเสาอากาศเข้ากับเครื่องขยายเสียง ในทำนองเดียวกันเสาอากาศรับสัญญาณที่มีความถี่ของ$f_l+f_c\pm f_d$ เมื่อตัวพลิกหน้ากระดาษเชื่อมต่อเสาอากาศเข้ากับ Mixer-II

• Mixer-II- มิกเซอร์สามารถสร้างผลรวมหรือความแตกต่างของความถี่ที่ใช้กับมัน สัญญาณที่มีความถี่$f_l+f_c\pm f_d$ และ $f_l$ถูกนำไปใช้กับ Mixer-II ที่นี่ Mixer-II ใช้สำหรับผลิตเอาต์พุตซึ่งมีความถี่$f_c\pm f_d$.

• IF Amplifier- เครื่องขยายเสียง IF ขยายสัญญาณความถี่กลาง (IF) เครื่องขยายเสียง IF ที่แสดงในรูปจะขยายสัญญาณที่มีความถี่$f_c+f_d$. สัญญาณขยายนี้ใช้เป็นอินพุตไปยังตัวตรวจจับเฟส

Phase Detector - ใช้ในการผลิตสัญญาณเอาต์พุตที่มีความถี่ $f_d$ จากสัญญาณอินพุตสองสัญญาณที่ใช้ซึ่งมีความถี่ของ $f_c+f_d$ และ $f_c$. เอาต์พุตของเครื่องตรวจจับเฟสสามารถเชื่อมต่อกับตัวยกเลิกสายล่าช้า

MTI Radar พร้อมเครื่องส่งสัญญาณ Power Oscillator

แผนภาพบล็อกของ MTI Radar พร้อมเครื่องส่งสัญญาณออสซิลเลเตอร์มีลักษณะคล้ายกับแผนภาพบล็อกของ MTI Radar พร้อมเครื่องส่งสัญญาณกำลังขยาย บล็อกที่ตรงกับส่วนรับจะเหมือนกันทั้งในบล็อกไดอะแกรม ในขณะที่บล็อกที่เกี่ยวข้องกับส่วนเครื่องส่งสัญญาณอาจแตกต่างกันทั้งในแผนภาพบล็อก

block diagram ของ MTI Radar พร้อมเครื่องส่งสัญญาณกำลังออสซิลเลเตอร์แสดงดังรูปต่อไปนี้

ดังแสดงในรูป MTI Radar ใช้เสาอากาศเดียวสำหรับทั้งการส่งและการรับสัญญาณด้วยความช่วยเหลือของ Duplexer operation ของ MTI Radar พร้อมเครื่องส่งสัญญาณกำลังออสซิลเลเตอร์มีการระบุไว้ด้านล่าง

• เอาต์พุตของ Magnetron Oscillator และเอาต์พุตของ Local Oscillator ถูกนำไปใช้กับ Mixer-I สิ่งนี้จะทำให้เกิดไฟล์IF signalเฟสที่เกี่ยวข้องโดยตรงกับเฟสของสัญญาณที่ส่ง

• เอาต์พุตของ Mixer-I ถูกนำไปใช้กับ Coherent Oscillator ดังนั้นเฟสของเอาต์พุต Coherent Oscillator จะเป็นlockedไปยังเฟสของสัญญาณ IF ซึ่งหมายความว่าเฟสของเอาต์พุต Coherent Oscillator จะเกี่ยวข้องโดยตรงกับเฟสของสัญญาณที่ส่ง

• ดังนั้นเอาต์พุตของ Coherent Oscillator สามารถใช้เป็นสัญญาณอ้างอิงเพื่อเปรียบเทียบสัญญาณสะท้อนที่ได้รับกับสัญญาณที่ส่งผ่านที่เกี่ยวข้องโดยใช้ phase detector.

งานข้างต้นจะถูกทำซ้ำสำหรับทุกสัญญาณที่ส่งใหม่

ระบบเรดาร์ - ตัวยกเลิกสายล่าช้า

ในบทนี้เราจะเรียนรู้เกี่ยวกับ Delay Line Cancellers ในระบบเรดาร์ ตามชื่อที่แนะนำเส้นดีเลย์จะแสดงความล่าช้าจำนวนหนึ่ง ดังนั้นเส้นหน่วงเวลาส่วนใหญ่จะใช้ในตัวยกเลิกสายล่าช้าเพื่อแนะนำไฟล์delay ของเวลาการทำซ้ำของชีพจร

Delay line cancellerเป็นตัวกรองซึ่งกำจัดส่วนประกอบ DC ของสัญญาณสะท้อนที่ได้รับจากเป้าหมายที่อยู่นิ่ง ซึ่งหมายความว่าอนุญาตให้ส่วนประกอบ AC ของสัญญาณสะท้อนที่ได้รับจากเป้าหมายที่ไม่อยู่นิ่งเช่นเป้าหมายเคลื่อนที่

ประเภทของ Delay Line Cancellers

ตัวยกเลิกสายล่าช้าสามารถแบ่งออกได้ดังต่อไปนี้ two types ตามจำนวนเส้นหน่วงเวลาที่มีอยู่

• Single Delay Line Canceller
• Double Delay Line Canceller

ในส่วนต่อไปเราจะพูดถึงเพิ่มเติมเกี่ยวกับตัวยกเลิกสายล่าช้าทั้งสองนี้

Single Delay Line Canceller

การรวมกันของเส้นหน่วงเวลาและตัวลบเรียกว่าตัวยกเลิกบรรทัดล่าช้า เรียกอีกอย่างว่า single Delay line Canceller block diagram ของตัวรับ MTI พร้อมตัวยกเลิกสาย Delay เดียวแสดงในรูปด้านล่าง

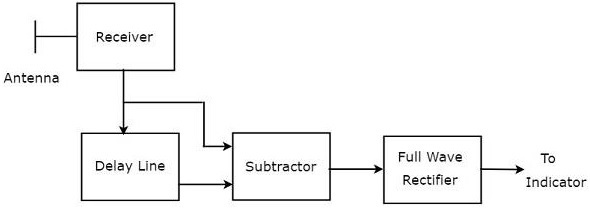
เราสามารถเขียนไฟล์ mathematical equation ของสัญญาณสะท้อนที่ได้รับหลังจากเอฟเฟกต์ Doppler เป็น -

$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:Equation\:1$$

ที่ไหน

A คือความกว้างของสัญญาณวิดีโอ

$f_d$ คือความถี่ Doppler

$\phi_o$ คือการกะระยะและเท่ากับ $4\pi f_tR_o/C$

เราจะได้รับไฟล์ output of Delay line cancellerโดยการแทนที่ $t$ โดย $t-T_P$ ในสมการที่ 1

$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:Equation\:2$$

ที่ไหน

$T_P$ คือเวลาในการทำซ้ำของชีพจร

เราจะได้รับไฟล์ subtractor output โดยการลบสมการ 2 ออกจากสมการ 1

$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$

$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$

$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:Equation\:3$$

เอาต์พุตของตัวลบถูกนำไปใช้เป็นอินพุตไปยัง Full Wave Rectifier ดังนั้นผลลัพธ์ของ Full Wave Rectifier จึงมีลักษณะดังแสดงในรูปต่อไปนี้ มันไม่มีอะไรนอกจากfrequency response ของตัวยกเลิกสายล่าช้าเดี่ยว

จากสมการที่ 3 เราสามารถสังเกตได้ว่าการตอบสนองความถี่ของตัวยกเลิกบรรทัดล่าช้าเดี่ยวจะกลายเป็นศูนย์เมื่อใด $\pi f_dT_P$ เท่ากับ integer multiples of $\pi$ ซึ่งหมายความว่า $\pi f_dT_P$ เท่ากับ $n\pi$ ในทางคณิตศาสตร์สามารถเขียนเป็น

$$\pi f_dT_P=n\pi$$

$$\Rightarrow f_dT_P=n$$

$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:Equation\:4$$

จากสมการที่ 4 เราสามารถสรุปได้ว่าการตอบสนองความถี่ของตัวยกเลิกบรรทัดล่าช้าเดี่ยวกลายเป็นศูนย์เมื่อความถี่ดอปเลอร์ $f_d$ เท่ากับจำนวนเต็มทวีคูณของเวลาการทำซ้ำพัลส์ซึ่งกันและกัน $T_P$.

เราทราบความสัมพันธ์ต่อไปนี้ระหว่างเวลาในการทำซ้ำของพัลส์และความถี่การทำซ้ำของพัลส์

$$f_d=\frac{1}{T_P}$$

$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:Equation\:5$$

เราจะได้สมการต่อไปนี้โดยแทนสมการ 5 ในสมการ 4

$$\Rightarrow f_d=nf_P\:\:\:\:\:Equation\:6$$

จากสมการที่ 6 เราสามารถสรุปได้ว่าการตอบสนองความถี่ของตัวยกเลิกบรรทัดล่าช้าเดี่ยวจะกลายเป็นศูนย์เมื่อความถี่ดอปเลอร์ $f_d$ เท่ากับจำนวนเต็มทวีคูณของความถี่การทำซ้ำพัลส์ $f_P$.

ความเร็วตาบอด

จากสิ่งที่เราเรียนรู้มาจนถึงตอนนี้ตัวยกเลิกสายหน่วงเวลาเดี่ยวจะกำจัดส่วนประกอบ DC ของสัญญาณสะท้อนที่ได้รับจากเป้าหมายที่อยู่นิ่งเมื่อ $n$เท่ากับศูนย์ นอกจากนั้นยังกำจัดส่วนประกอบ AC ของสัญญาณเสียงสะท้อนที่ได้รับจากเป้าหมายที่ไม่อยู่นิ่งเมื่อความถี่ Doppler$f_d$ เท่ากับจำนวนเต็ม (other than zero) ความถี่การทำซ้ำพัลส์ทวีคูณ $f_P$.

ดังนั้นความเร็วสัมพัทธ์ที่การตอบสนองความถี่ของตัวยกเลิกบรรทัดล่าช้าเดี่ยวจะกลายเป็นศูนย์จึงถูกเรียก blind speeds. ในทางคณิตศาสตร์เราสามารถเขียนนิพจน์สำหรับความเร็วตาบอดได้$v_n$ เป็น -

$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:Equation\:7$$

$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:Equation\:8$$

ที่ไหน

$n$ เป็นจำนวนเต็มและเท่ากับ 1, 2, 3 และอื่น ๆ

$\lambda$ คือความยาวคลื่นปฏิบัติการ

ตัวอย่างปัญหา

MTI Radar ทำงานที่ความถี่ $6GHZ$ ด้วยความถี่การทำซ้ำของพัลส์ $1KHZ$. ค้นหาที่หนึ่งสองและสามblind speeds ของเรดาร์นี้

วิธีการแก้

ให้

ความถี่ในการทำงานของ MTI Radar $f=6GHZ$

ความถี่การทำซ้ำของพัลส์ $f_P=1KHZ$.

ต่อไปนี้เป็นสูตรสำหรับ operating wavelength $\lambda$ ในแง่ของความถี่ในการทำงาน f.

$$\lambda=\frac{C}{f}$$

ทดแทน $C=3\times10^8m/sec$ และ $f=6GHZ$ ในสมการข้างต้น

$$\lambda=\frac{3\times10^8}{6\times10^9}$$

$$\Rightarrow \lambda=0.05m$$

ดังนั้น operating wavelength $\lambda$ เท่ากับ $0.05m$เมื่อความถี่ในการทำงาน f คือ $6GHZ$.

เราทราบสิ่งต่อไปนี้ formula for blind speed.

$$v_n=\frac{n\lambda f_p}{2}$$

โดยการแทนที่ $n$= 1,2 & 3 ในสมการด้านบนเราจะได้สมการต่อไปนี้สำหรับความเร็วตาบอดแรกวินาทีและสามตามลำดับ

$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$

$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$

$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$

Substitute ค่าของ $\lambda$ และ $f_P$ ในสมการของความเร็วตาบอดแรก

$$v_1=\frac{0.05\times 10^3}{2}$$

$$\Rightarrow v_1=25m/sec$$

ดังนั้นไฟล์ first blind speed $v_1$ เท่ากับ $25m/sec$ สำหรับข้อกำหนดที่กำหนด

เราจะได้รับค่าของ second & third blind speeds เช่น $50m/sec$& $75m/sec$ ตามลำดับโดยแทนที่ค่าของð ?? '1 ปอนด์ในสมการของความเร็วตาบอดที่สองและสาม

Double Delay Line Canceller

เรารู้ว่าตัวยกเลิกบรรทัดล่าช้าเดี่ยวประกอบด้วยเส้นหน่วงเวลาและตัวลบ หากตัวยกเลิกสายล่าช้าดังกล่าวสองตัวเรียงต่อกันจะเรียกชุดค่าผสมนั้นเรียกว่าตัวยกเลิกสายหน่วงเวลาคู่ block diagram ของตัวยกเลิกสายล่าช้าสองเท่าจะแสดงในรูปต่อไปนี้

ปล่อย $p\left ( t \right )$ และ $q\left ( t \right )$เป็นอินพุตและเอาต์พุตของตัวยกเลิกบรรทัดการหน่วงเวลาแรก เราจะได้รับความสัมพันธ์ทางคณิตศาสตร์ต่อไปนี้จากfirst delay line canceller.

$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:Equation\:9$$

เอาต์พุตของตัวยกเลิกบรรทัดการหน่วงเวลาแรกถูกนำไปใช้เป็นอินพุตไปยังตัวยกเลิกบรรทัดหน่วงเวลาที่สอง ดังนั้น$q\left ( t \right )$จะเป็นอินพุตของตัวยกเลิกบรรทัดล่าช้าที่สอง ปล่อย$r\left ( t \right )$เป็นเอาต์พุตของตัวยกเลิกบรรทัดล่าช้าที่สอง เราจะได้รับความสัมพันธ์ทางคณิตศาสตร์ต่อไปนี้จากsecond delay line canceller.

$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:Equation\:10$$

แทนที่ $t$ โดย $t-T_P$ ในสมการ 9.

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$

$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:Equation\:11$$

Substitute, สมการ 9 และสมการ 11 ในสมการ 10.

$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$

$$\Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:Equation\:12$$

advantageของตัวยกเลิกสายล่าช้าสองครั้งคือมันจะปฏิเสธความยุ่งเหยิงในวงกว้าง เอาต์พุตของตัวยกเลิกสายหน่วงเวลาสองตัวซึ่งเรียงซ้อนกันจะเท่ากับกำลังสองของเอาต์พุตของตัวยกเลิกสายหน่วงเวลาเดี่ยว

ดังนั้นขนาดของเอาต์พุตของตัวยกเลิกการหน่วงเวลาคู่ซึ่งมีอยู่ที่ตัวรับสัญญาณเรดาร์ MTI จะเท่ากับ $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$.

ลักษณะการตอบสนองความถี่ของตัวยกเลิกสายการหน่วงเวลาสองครั้งและการรวมกันของตัวยกเลิกสายการหน่วงเวลาสองสายจะเหมือนกัน advantage ตัวยกเลิกบรรทัดล่าช้าของโดเมนเวลาคือสามารถใช้งานได้กับทุกช่วงความถี่

ระบบเรดาร์ - เรดาร์ติดตาม

เรดาร์ซึ่งใช้ในการติดตามเส้นทางของเป้าหมายหนึ่งหรือหลายเป้าหมายเรียกว่า Tracking Radar. โดยทั่วไปจะทำหน้าที่ต่อไปนี้ก่อนที่จะเริ่มกิจกรรมการติดตาม

• การตรวจจับเป้าหมาย
• ช่วงของเป้าหมาย
• การหามุมเงยและมุมแอซิมัท
• ค้นหา Doppler frequency shift

ดังนั้นเรดาร์ติดตามจะติดตามเป้าหมายโดยการติดตามหนึ่งในสามพารามิเตอร์ ได้แก่ ช่วงมุมการเปลี่ยนความถี่ดอปเลอร์ เรดาร์ติดตามส่วนใหญ่ใช้นามสกุลprinciple of tracking in angle. ตอนนี้ให้เราคุยกันว่าการติดตามเชิงมุมคืออะไร

การติดตามเชิงมุม

คานดินสอของเสาอากาศเรดาร์ทำการติดตามในมุม แกนของเสาอากาศเรดาร์ถือเป็นทิศทางอ้างอิง หากทิศทางของเป้าหมายและทิศทางอ้างอิงไม่เหมือนกันก็จะมีangular errorซึ่งไม่มีอะไรนอกจากความแตกต่างระหว่างสองทิศทาง

หากสัญญาณผิดพลาดเชิงมุมถูกนำไปใช้กับระบบควบคุมเซอร์โวสัญญาณจะเคลื่อนแกนของเสาอากาศเรดาร์ไปยังทิศทางของเป้าหมาย ทั้งแกนของเสาอากาศเรดาร์และทิศทางของเป้าหมายจะcoincideเมื่อข้อผิดพลาดเชิงมุมเป็นศูนย์ มีกลไกป้อนกลับในเรดาร์ติดตามซึ่งทำงานจนกว่าข้อผิดพลาดเชิงมุมจะกลายเป็นศูนย์

ต่อไปนี้คือไฟล์ two techniquesซึ่งใช้ในการติดตามเชิงมุม

• Lobing ตามลำดับ
• การสแกนรูปกรวย

ตอนนี้ให้เราพูดคุยเกี่ยวกับสองเทคนิคนี้ทีละคน

Lobing ตามลำดับ

หากคานเสาอากาศถูกสลับระหว่างสองรูปแบบสลับกันเพื่อติดตามเป้าหมายจะเรียกว่า sequential lobing. เรียกอีกอย่างว่าการสลับตามลำดับและการสลับกลีบ เทคนิคนี้ใช้เพื่อค้นหาข้อผิดพลาดเชิงมุมในพิกัดเดียว ให้รายละเอียดทั้งขนาดและทิศทางของข้อผิดพลาดเชิงมุม

รูปต่อไปนี้แสดงตัวอย่างของการเรียงลำดับตามลำดับใน polar coordinates.

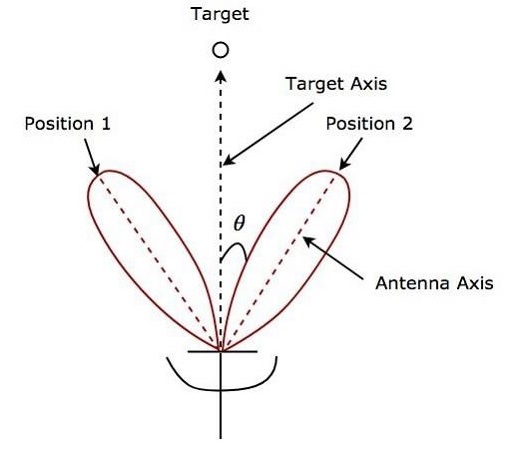
ดังแสดงในรูปคานเสาอากาศจะสลับไปมาระหว่างตำแหน่ง 1 และตำแหน่ง 2 สลับกัน ข้อผิดพลาดเชิงมุมθระบุไว้ในรูปด้านบน การล็อกตามลำดับทำให้ตำแหน่งของเป้าหมายมีความแม่นยำสูง นี่คือหลักadvantage ของ lobing ตามลำดับ

การสแกนรูปกรวย

หากลำแสงของเสาอากาศหมุนอย่างต่อเนื่องเพื่อติดตามเป้าหมายจะเรียกว่า conical scanning. การมอดูเลตการสแกนทรงกรวยใช้เพื่อค้นหาตำแหน่งของเป้าหมาย รูปต่อไปนี้แสดงตัวอย่างของการสแกนรูปกรวย

Squint angleคือมุมระหว่างแกนลำแสงและแกนหมุนซึ่งแสดงในรูปด้านบน สัญญาณสะท้อนที่ได้รับจากเป้าหมายจะถูกมอดูเลตที่ความถี่เท่ากับความถี่ที่ลำแสงของเสาอากาศหมุน

มุมระหว่างทิศทางของชิ้นงานและแกนหมุนเป็นตัวกำหนด amplitude of the modulated signal. ดังนั้นการมอดูเลตการสแกนรูปกรวยจึงต้องถูกแยกออกจากสัญญาณสะท้อนจากนั้นจึงนำไปใช้กับระบบควบคุมเซอร์โวซึ่งจะเคลื่อนแกนลำแสงเสาอากาศไปยังทิศทางของเป้าหมาย

ระบบเรดาร์ - พารามิเตอร์เสาอากาศ

อัน Antenna หรือแอเรียลเป็นตัวแปลงสัญญาณซึ่งแปลงพลังงานไฟฟ้าเป็นคลื่นแม่เหล็กไฟฟ้าและในทางกลับกัน

เสาอากาศมีพารามิเตอร์ต่อไปนี้ -

• Directivity
• ประสิทธิภาพของรูรับแสง
• ประสิทธิภาพของเสาอากาศ
• Gain

ตอนนี้ให้เราพูดคุยเกี่ยวกับพารามิเตอร์เหล่านี้โดยละเอียด -

ทิศทาง

ตามคำจำกัดความมาตรฐาน“ อัตราส่วนของความเข้มรังสีสูงสุดของวัตถุเสาอากาศต่อความเข้มการแผ่รังสีของเสาอากาศแบบไอโซโทรปิกหรือเสาอากาศอ้างอิงการแผ่พลังงานทั้งหมดที่เท่ากันเรียกว่า Directivity.”

แม้ว่าเสาอากาศจะแผ่พลังออกมา แต่ทิศทางที่มันแผ่กระจายออกไปนั้นมีความสำคัญมาก เสาอากาศที่อยู่ระหว่างการศึกษาเรียกว่าsubject Antenna. ความเข้มของรังสีจะโฟกัสไปในทิศทางใดทิศทางหนึ่งในขณะที่กำลังส่งหรือรับ ดังนั้นเสาอากาศจึงถูกกล่าวว่ามีทิศทางในทิศทางนั้น ๆ

• อัตราส่วนของความเข้มของรังสีในทิศทางที่กำหนดจากเสาอากาศต่อความเข้มของรังสีโดยเฉลี่ยในทุกทิศทางเรียกว่า Directivity.

• หากไม่ได้ระบุทิศทางนั้นไว้ทิศทางที่สังเกตความเข้มสูงสุดสามารถใช้เป็นทิศทางของเสาอากาศนั้นได้

• ทิศทางของเสาอากาศที่ไม่ใช่ไอโซทรอปิกจะเท่ากับอัตราส่วนของความเข้มของรังสีในทิศทางที่กำหนดกับความเข้มของรังสีของแหล่งกำเนิดไอโซทรอปิก

Mathematicallyเราสามารถเขียนนิพจน์สำหรับ Directivity เป็น -

$$Directivity=\frac{U_{Max}\left (\theta,\phi\right )}{U_0}$$

ที่ไหน

$U_{Max}\left (\theta,\phi\right )$ คือความเข้มรังสีสูงสุดของเสาอากาศของวัตถุ

$U_0$ คือความเข้มการแผ่รังสีของเสาอากาศแบบไอโซทรอปิก

ประสิทธิภาพของรูรับแสง

ตามข้อกำหนดมาตรฐาน “Aperture efficiency ของเสาอากาศคืออัตราส่วนของพื้นที่การแผ่รังสีที่มีประสิทธิภาพ (หรือพื้นที่ที่มีประสิทธิภาพ) กับพื้นที่ทางกายภาพของรูรับแสง”

เสาอากาศแผ่พลังผ่านรูรับแสง รังสีนี้ควรมีประสิทธิภาพโดยมีการสูญเสียน้อยที่สุด ควรคำนึงถึงพื้นที่ทางกายภาพของรูรับแสงด้วยเนื่องจากประสิทธิภาพของการแผ่รังสีขึ้นอยู่กับพื้นที่ของรูรับแสงทางกายภาพบนเสาอากาศ

Mathematicallyเราสามารถเขียนนิพจน์สำหรับประสิทธิภาพของรูรับแสง $\epsilon_A$ เช่น

$$\epsilon _A=\frac{A_{eff}}{A_p}$$

ที่ไหน

$A_{eff}$ เป็นพื้นที่ที่มีประสิทธิภาพ

$A_P$ เป็นพื้นที่ทางกายภาพ

ประสิทธิภาพของเสาอากาศ

ตามข้อกำหนดมาตรฐาน “Antenna Efficiency คืออัตราส่วนของกำลังการแผ่รังสีของเสาอากาศต่อกำลังไฟฟ้าเข้าที่เสาอากาศยอมรับ”

เสาอากาศใด ๆ ได้รับการออกแบบให้แผ่พลังงานโดยมีการสูญเสียน้อยที่สุดสำหรับอินพุตที่กำหนด ประสิทธิภาพของเสาอากาศอธิบายว่าเสาอากาศสามารถส่งออกได้อย่างมีประสิทธิภาพมากเพียงใดโดยมีการสูญเสียขั้นต่ำในสายส่ง เรียกอีกอย่างว่าRadiation Efficiency Factor ของเสาอากาศ

Mathematicallyเราสามารถเขียนนิพจน์สำหรับประสิทธิภาพของเสาอากาศ 𝜂𝑒 เป็น -

$$\eta _e=\frac{P_{Rad}}{P_{in}}$$

ที่ไหน

$P_{Rad}$ คือปริมาณพลังงานที่แผ่ออกมา

$P_{in}$ คือกำลังไฟฟ้าเข้าสำหรับเสาอากาศ

กำไร

ตามข้อกำหนดมาตรฐาน “Gain ของเสาอากาศคืออัตราส่วนของความเข้มของการแผ่รังสีในทิศทางที่กำหนดกับความเข้มของรังสีที่จะได้รับหากพลังงานที่เสาอากาศยอมรับได้ถูกแผ่ออกไปแบบไอโซทรอปิก "

เพียงแค่ Gainของเสาอากาศคำนึงถึงทิศทางของเสาอากาศควบคู่ไปกับประสิทธิภาพที่มีประสิทธิภาพ หากพลังงานที่เสาอากาศยอมรับได้ถูกแผ่ออกไปแบบไอโซทรอปิก (นั่นหมายถึงในทุกทิศทาง) ความเข้มของรังสีที่เราได้รับสามารถนำมาเป็นค่าอ้างอิงได้

• ระยะ Antenna gain อธิบายว่ากำลังส่งไปในทิศทางของการแผ่รังสีสูงสุดไปยังแหล่งกำเนิดไอโซโทรปิก

• มักจะวัดเป็น dB.

• ซึ่งแตกต่างจาก Directivity การเพิ่มของเสาอากาศจะคำนึงถึงความสูญเสียที่เกิดขึ้นด้วยดังนั้นจึงมุ่งเน้นไปที่ประสิทธิภาพ

Mathematicallyเราสามารถเขียนนิพจน์สำหรับ Antenna Gain $G$ เป็น -

$$G=\eta_eD$$

ที่ไหน

$\eta_e$ คือประสิทธิภาพของเสาอากาศ

$D$ คือทิศทางของเสาอากาศ

ระบบเรดาร์ - เสาอากาศเรดาร์

ในบทนี้ให้เราเรียนรู้เกี่ยวกับเสาอากาศซึ่งมีประโยชน์ในการสื่อสารด้วยเรดาร์ เราสามารถแบ่งประเภทของเสาอากาศเรดาร์ได้ดังต่อไปนี้two types ขึ้นอยู่กับโครงสร้างทางกายภาพ

• เสาอากาศสะท้อนแสงแบบพาราโบลา
• เสาอากาศเลนส์

ในส่วนต่อไปเราจะพูดถึงเสาอากาศทั้งสองประเภทโดยละเอียด

เสาอากาศสะท้อนแสงแบบพาราโบลา

Parabolic Reflector Antennas คือเสาอากาศไมโครเวฟ ความรู้เกี่ยวกับตัวสะท้อนแสงพาราโบลาเป็นสิ่งสำคัญที่จะต้องทำความเข้าใจเกี่ยวกับการทำงานของเสาอากาศในเชิงลึก

หลักการทำงาน

Parabola ไม่มีอะไรนอกจาก Locus ของจุดซึ่งเคลื่อนที่ในลักษณะที่ระยะห่างจากจุดคงที่ (เรียกว่าโฟกัส) บวกระยะทางจากเส้นตรง (เรียกว่า directrix) เป็นค่าคงที่

รูปต่อไปนี้แสดงไฟล์ geometry of parabolic reflector. จุด F และ V คือโฟกัส (ให้ฟีด) และจุดยอดตามลำดับ เส้นเชื่อม F และ V เป็นแกนสมมาตร$P_1Q_1, P_2Q_2$ และ $P_3Q_3$คือรังสีสะท้อน เส้น L แสดงถึงเส้นตรงที่จุดสะท้อนอยู่ (เพื่อบอกว่ากำลังเรียงกัน)

ดังแสดงในรูประยะห่างระหว่าง F และ L คงที่เมื่อเทียบกับคลื่นที่ถูกโฟกัส คลื่นสะท้อนก่อตัวเป็นรูปคลื่นโคลิเมตด้านหน้าออกจากรูปพาราโบลา อัตราส่วนของทางยาวโฟกัสต่อขนาดรูรับแสง (กล่าวคือ$f/D$ ) เรียกว่า “f over D ratio”. เป็นพารามิเตอร์ที่สำคัญของตัวสะท้อนแสงพาราโบลาและค่าของมันแตกต่างกันไป0.25 to 0.50.

law of reflectionระบุว่ามุมตกกระทบและมุมสะท้อนเท่ากัน กฎนี้เมื่อใช้ร่วมกับพาราโบลาช่วยให้ลำแสงโฟกัส รูปร่างของพาราโบลาเมื่อใช้เพื่อจุดประสงค์ในการสะท้อนของคลื่นแสดงคุณสมบัติบางอย่างของพาราโบลาซึ่งเป็นประโยชน์ในการสร้างเสาอากาศโดยใช้คลื่นที่สะท้อน

คุณสมบัติของพาราโบลา

ต่อไปนี้เป็นคุณสมบัติที่แตกต่างกันของ Parabola -

• คลื่นทั้งหมดที่เกิดจากโฟกัสสะท้อนกลับไปที่แกนพาราโบลา ดังนั้นคลื่นทั้งหมดที่มาถึงรูรับแสงจึงอยู่ในเฟส

• ในขณะที่คลื่นอยู่ในเฟสลำแสงของรังสีตามแกนพาราโบลาจะแข็งแรงและเข้มข้น

ตามจุดเหล่านี้ตัวสะท้อนแสงพาราโบลาช่วยในการสร้างทิศทางที่สูงด้วยความกว้างของลำแสงที่แคบลง

การก่อสร้างและการทำงานของ Parabolic Reflector

หากใช้เสาอากาศแบบ Parabolic Reflector สำหรับ transmitting a signalสัญญาณจากฟีดจะออกมาจากเสาอากาศแบบไดโพลหรือเสาอากาศฮอร์นเพื่อโฟกัสคลื่นไปที่พาราโบลา หมายความว่าคลื่นจะออกมาจากจุดโฟกัสและกระทบกับตัวสะท้อนพาราโบลา ตอนนี้คลื่นนี้ได้รับการสะท้อนให้เห็นเป็นคลื่นด้านหน้าตามที่กล่าวไว้ก่อนหน้านี้เพื่อรับการส่ง

ใช้เสาอากาศเดียวกันเป็นไฟล์ receiver. เมื่อคลื่นแม่เหล็กไฟฟ้ากระทบรูปร่างของพาราโบลาคลื่นจะสะท้อนไปยังจุดป้อน เสาอากาศไดโพลหรือเสาอากาศฮอร์นซึ่งทำหน้าที่เป็นเสาอากาศรับสัญญาณที่ฟีดจะรับสัญญาณนี้เพื่อแปลงเป็นสัญญาณไฟฟ้าและส่งต่อไปยังวงจรรับ

การได้รับของพาราโบลาเป็นหน้าที่ของอัตราส่วนรูรับแสง $D/\lambda$. พลังการแผ่รังสีที่มีประสิทธิภาพ(ERP) ของเสาอากาศคือการคูณของกำลังอินพุตที่ป้อนให้กับเสาอากาศและกำลังไฟฟ้าที่เพิ่มขึ้น

โดยปกติเสาอากาศแตรนำคลื่นจะใช้เป็นตัวป้อนสำหรับเสาอากาศสะท้อนแสงพาราโบลา นอกจากเทคนิคนี้แล้วเรายังมีฟีดสองประเภทต่อไปนี้ที่มอบให้กับเสาอากาศสะท้อนแสงพาราโบลา

• ฟีด Cassegrain
• ฟีดเกรกอเรียน

ฟีด Cassegrain

ในประเภทนี้ฟีดจะอยู่ที่จุดยอดของพาราโบลาซึ่งแตกต่างจากตัวสะท้อนพาราโบลา แผ่นสะท้อนแสงรูปทรงนูนซึ่งทำหน้าที่เป็นไฮเปอร์โบลอยด์วางอยู่ตรงข้ามกับฟีดของเสาอากาศ เป็นที่รู้จักกันในชื่อsecondary hyperboloid reflectorหรือตัวสะท้อนแสงย่อย มันถูกวางไว้ในลักษณะที่จุดโฟกัสจุดหนึ่งตรงกับโฟกัสของพาราโบลา ดังนั้นคลื่นจึงสะท้อนสองครั้ง

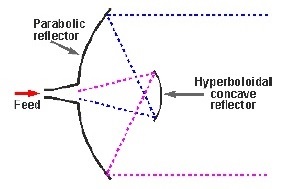
รูปด้านบนแสดงรูปแบบการทำงานของฟีด cassegrain

ฟีดเกรกอเรียน

ประเภทของฟีดที่มีคู่ของการกำหนดค่าบางอย่างอยู่ที่นั่นและความกว้างของลำแสงฟีดจะเพิ่มขึ้นเรื่อย ๆ ในขณะที่ขนาดของเสาอากาศถูกยึดไว้คงที่เรียกว่า Gregorian feed. ที่นี่ไฮเพอร์โบลอยด์รูปนูนของ Cassegrain จะถูกแทนที่ด้วยตัวสะท้อนแสงพาราโบลารูปเว้าซึ่งแน่นอนว่ามีขนาดเล็กกว่า

ตัวสะท้อนแสงประเภทฟีดเกรกอเรียนเหล่านี้สามารถใช้ได้ในสี่วิธีต่อไปนี้ -

• ระบบเกรกอเรียนใช้รีเฟลกเตอร์รีเฟลกเตอร์รีเฟลกเตอร์ย่อยที่ foci F1

• ระบบเกรกอเรียนใช้รีเฟลกเตอร์รีเฟลกเตอร์รีเฟลกเตอร์ย่อยที่ foci F2

• ระบบ Cassegrain โดยใช้ตัวสะท้อนแสงแบบไฮเปอร์โบลอยด์ (นูน)

• ระบบ Cassegrain โดยใช้ตัวสะท้อนแสงแบบไฮเปอร์โบลอยด์ (เว้า แต่ฟีดอยู่ใกล้กับมันมาก)

ในบรรดาเสาอากาศสะท้อนแสงประเภทต่างๆตัวสะท้อนแสงพาราโบลาแบบง่ายและตัวสะท้อนแสงพาราโบลาฟีด Cassegrain เป็นตัวสะท้อนแสงที่ใช้กันมากที่สุด

เสาอากาศเลนส์

เสาอากาศของเลนส์ใช้พื้นผิวโค้งสำหรับทั้งการส่งและรับสัญญาณ เสาอากาศเหล่านี้ประกอบด้วยแก้วซึ่งจะมีคุณสมบัติในการบรรจบกันและการเบี่ยงเบนของเลนส์ frequency range การใช้งานเสาอากาศเลนส์เริ่มต้นที่ 1 GHz แต่การใช้งานนั้นมากกว่าที่ 3 GHz and above.

จำเป็นต้องมีความรู้เกี่ยวกับเลนส์เพื่อทำความเข้าใจการทำงานของเสาอากาศเลนส์ในเชิงลึก จำไว้ว่าเลนส์แก้วปกติใช้งานได้กับprinciple of refraction.

การก่อสร้างและการทำงานของเสาอากาศเลนส์

หากมีการสันนิษฐานว่าแหล่งกำเนิดแสงอยู่ที่จุดโฟกัสของเลนส์ซึ่งอยู่ที่ระยะโฟกัสจากเลนส์รังสีจะผ่านเลนส์ไปในลักษณะที่มีการรวมกันหรือ parallel rays ที่ด้านหน้าคลื่นระนาบ

มีสองปรากฏการณ์ที่เกิดขึ้นเมื่อรังสีตกจากด้านต่างๆของเลนส์ พวกเขาได้รับที่นี่ -

• รังสีที่ผ่านศูนย์กลางของเลนส์จะหักเหน้อยกว่ารังสีที่ผ่านขอบของเลนส์ รังสีทั้งหมดจะถูกส่งขนานกับคลื่นระนาบด้านหน้า ปรากฏการณ์ของเลนส์นี้เรียกว่าDivergence.

• ขั้นตอนเดียวกันนี้จะย้อนกลับหากลำแสงถูกส่งจากด้านขวาไปยังด้านซ้ายของเลนส์เดียวกัน จากนั้นลำแสงจะหักเหและมาบรรจบกันที่จุดที่เรียกว่าจุดโฟกัสที่ระยะโฟกัสจากเลนส์ ปรากฏการณ์นี้เรียกว่าConvergence.

แผนภาพต่อไปนี้จะช่วยให้เราเข้าใจปรากฏการณ์ได้ดีขึ้น

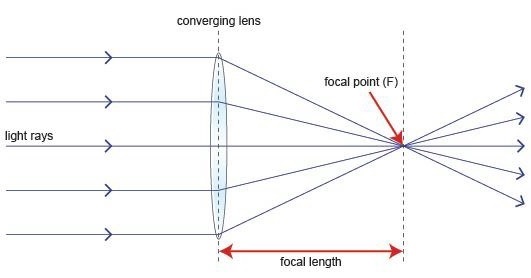
ray diagramแทนจุดโฟกัสและทางยาวโฟกัสจากแหล่งสัญญาณไปยังเลนส์ รังสีขนานที่ได้รับเรียกอีกอย่างว่ารังสีโคลิเมต

ในรูปด้านบนแหล่งที่มาที่จุดโฟกัสที่ระยะโฟกัสจากเลนส์จะถูกจับคู่กันที่ด้านหน้าของคลื่นระนาบ ปรากฏการณ์นี้สามารถย้อนกลับได้ซึ่งหมายความว่าแสงหากส่งจากด้านซ้ายจะมาบรรจบกันที่ด้านขวาของเลนส์

มันเป็นเพราะเหตุนี้ reciprocityเลนส์สามารถใช้เป็นเสาอากาศได้เนื่องจากปรากฏการณ์เดียวกันนี้ช่วยในการใช้เสาอากาศเดียวกันสำหรับทั้งการส่งและการรับ

เพื่อให้ได้คุณสมบัติการโฟกัสที่ความถี่สูงขึ้นดัชนีการหักเหของแสงควรน้อยกว่าเอกภาพ ไม่ว่าดัชนีการหักเหของแสงจะเป็นอย่างไรจุดประสงค์ของเลนส์คือการปรับรูปคลื่นให้ตรง ด้วยเหตุนี้เลนส์ E-plane และ H-plane จึงได้รับการพัฒนาซึ่งทำให้หน้าคลื่นล่าช้าหรือเร็วขึ้นด้วย

ระบบเรดาร์ - ตัวรับตัวกรองที่ตรงกัน

หากตัวกรองสร้างเอาต์พุตในลักษณะที่เพิ่มอัตราส่วนของกำลังสูงสุดของเอาต์พุตเพื่อหมายถึงพลังเสียงในการตอบสนองความถี่ตัวกรองนั้นจะเรียกว่า Matched filter.

นี่เป็นเกณฑ์สำคัญซึ่งพิจารณาในขณะออกแบบเครื่องรับเรดาร์ ในบทนี้ให้เราพูดถึงฟังก์ชันตอบสนองความถี่ของตัวกรองที่ตรงกันและการตอบสนองแรงกระตุ้นของตัวกรองที่ตรงกัน

ฟังก์ชันตอบสนองความถี่ของตัวกรองที่ตรงกัน

การตอบสนองความถี่ของฟิลเตอร์ที่ตรงกันจะเป็นสัดส่วนกับคอนจูเกตที่ซับซ้อนของสเปกตรัมของสัญญาณอินพุต ในทางคณิตศาสตร์เราสามารถเขียนนิพจน์สำหรับfrequency response function, $H\left (f\right )$ ของตัวกรองที่ตรงกันเป็น -

$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:1$$

ที่ไหน

$G_a$ คือกำไรสูงสุดของตัวกรองที่ตรงกัน

$S\left (f\right )$ คือการแปลงฟูเรียร์ของสัญญาณอินพุต $s\left (t\right )$

$S^\ast\left (f\right )$ คือคอนจูเกตที่ซับซ้อนของ $S\left (f\right )$

$t_1$ คือเวลาทันทีที่สัญญาณสังเกตได้ว่ามีค่าสูงสุด

โดยทั่วไปค่าของ $G_a$ถือเป็นหนึ่งเดียว เราจะได้สมการต่อไปนี้โดยการแทนที่$G_a=1$ ในสมการที่ 1

$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:2$$

ฟังก์ชั่นตอบสนองความถี่ $H\left (f\right )$ ของตัวกรองที่ตรงกันกำลังมีไฟล์ magnitude ของ $S^\ast\left (f\right )$ และ phase angle ของ $e^{-j2\pi ft_1}$ซึ่งแตกต่างกันไปตามความถี่

การตอบสนองต่อแรงกระตุ้นของตัวกรองที่ตรงกัน

ใน time domainเราจะได้ผลลัพธ์ $h(t)$ of Matched filter receiver by applying the inverse Fourier transform of the frequency response function, $H(f)$.

$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:Equation\:3$$

Substitute, Equation 1 in Equation 3.

$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:Equation\:4$$

We know the following relation.

$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:Equation\:5$$

Substitute, Equation 5 in Equation 4.

$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$

$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:Equation\:6$$

In general, the value of $G_a$ is considered as one. We will get the following equation by substituting $G_a=1$ in Equation 6.

$$h(t)=s\left (t_1-t\right )$$

The above equation proves that the impulse response of Matched filter is the mirror image of the received signal about a time instant $t_1$. The following figures illustrate this concept.

The received signal, $s\left (t\right )$ and the impulse response, $h\left (t\right )$ of the matched filter corresponding to the signal, $s\left (t\right )$ are shown in the above figures.

Radar Systems - Radar Displays

An electronic instrument, which is used for displaying the data visually is known as display. So, the electronic instrument which displays the information about Radar’s target visually is known as Radar display. It shows the echo signal information visually on the screen.

Types of Radar Displays

In this section, we will learn about the different types of Radar Displays. The Radar Displays can be classified into the following types.

A-Scope

It is a two dimensional Radar display. The horizontal and vertical coordinates represent the range and echo amplitude of the target respectively. In A-Scope, the deflection modulation takes place. It is more suitable for manually tracking Radar.

B-Scope

It is a two dimensional Radar display. The horizontal and vertical coordinates represent the azimuth angle and the range of the target respectively. In B-Scope, intensity modulation takes place. It is more suitable for military Radars.

C-Scope

It is a two-dimensional Radar display. The horizontal and vertical coordinates represent the azimuth angle and elevation angle respectively. In C-Scope, intensity modulation takes place.

D-Scope

If the electron beam is deflected or the intensity-modulated spot appears on the Radar display due to the presence of target, then it is known as blip. C-Scope becomes D-Scope, when the blips extend vertically in order to provide the distance.

E-Scope

It is a two-dimensional Radar display. The horizontal and vertical coordinates represent the distance and elevation angle respectively. In E-Scope, intensity modulation takes place.

F-Scope

If the Radar Antenna is aimed at the target, then F-Scope displays the target as a centralized blip. So, the horizontal and vertical displacements of the blip represent the horizontal and vertical aiming errors respectively.

G-Scope

If the Radar Antenna is aimed at the target, then G-Scope displays the target as laterally centralized blip. The horizontal and vertical displacements of the blip represent the horizontal and vertical aiming errors respectively.

H-Scope

It is the modified version of B-Scope in order to provide the information about elevation angle of the target. It displays the target as two blips, which are closely spaced. This can be approximated to a short bright line and the slope of this line will be proportional to the sine of the elevation angle.

I-Scope

If the Radar Antenna is aimed at the target, then I-Scope displays the target as a circle. The radius of this circle will be proportional to the distance of the target. If the Radar Antenna is aimed at the target incorrectly, then I-Scope displays the target as a segment instead of circle. The arc length of that segment will be inversely proportional to the magnitude of pointing error.

J-Scope

It is the modified version of A-Scope. It displays the target as radial deflection from time base.

K-Scope

It is the modified version of A-Scope. If the Radar Antenna is aimed at the target, then K-Scope displays the target as a pair of vertical deflections, which are having equal height. If the Radar Antenna is aimed at the target incorrectly, then there will be pointing error. So, the magnitude and the direction of the pointing error depends on the difference between the two vertical deflections.

L-Scope

If the Radar Antenna is aimed at the target, then L-Scope displays the target as two horizontal blips having equal amplitude. One horizontal blip lies to the right of central vertical time base and the other one lies to the left of central vertical time base.

M-Scope

It is the modified version of A-Scope. An adjustable pedestal signal has to be moved along the baseline till it coincides the signal deflections, which are coming from the horizontal position of the target. In this way, the target’s distance can be determined.

N-Scope

It is the modified version of K-Scope. An adjustable pedestal signal is used for measuring distance.

O-Scope

It is the modified version of A-Scope. We will get O-Scope, by including an adjustable notch to A-Scope for measuring distance.

P-Scope

It is a Radar display, which uses intensity modulation. It displays the information of echo signal as plan view. Range and azimuth angle are displayed in polar coordinates. Hence, it is called the Plan Position Indicator or the PPI display.

R-Scope

It is a Radar display, which uses intensity modulation. The horizontal and vertical coordinates represent the range and height of the target respectively. Hence, it is called Range-Height Indicator or RHI display.

Radar Systems - Duplexers

In two-way communication, if we are supposed to use the same Antenna for both transmission and reception of the signals, then we require Duplexer. Duplexer is a microwave switch, which connects the Antenna to the transmitter section for transmission of the signal. Therefore, the Radar cannot receive the signal during transmission time.

Similarly, it connects the Antenna to the receiver section for the reception of the signal. The Radar cannot transmit the signal during reception time. In this way, Duplexer isolates both transmitter and receiver sections.

Types of Duplexers

In this section, we will learn about the different types of duplexers. We can classify the Duplexers into the following three types.

• Branch-type Duplexer
• Balanced Duplexer
• Circulator as Duplexer

In our subsequent sections, we will discuss the types of Duplexers in detail.

Branch-type Duplexer

Branch-type Duplexer consists of two switches — Transmit-Receive (TR) switch and Anti Transmit-Receive (ATR) switch. The following figure shows the block diagram of Branch-type Duplexer −

As shown in the figure, the two switches, TR & ATR are placed at a distance of $\lambda/4$ from the transmission line and both the switches are separated by a distance of $\lambda/4$. The working of Branch-type Duplexer is mentioned below.

• During transmission, both TR & ATR will look like an open circuit from the transmission line. Therefore, the Antenna will be connected to the transmitter through transmission line.

• During reception, ATR will look like a short circuit across the transmission line. Hence, Antenna will be connected to the receiver through transmission line.

The Branch-type Duplexer is suitable only for low cost Radars, since it is having less power handling capability.

Balanced Duplexer

We know that a two-hole Directional Coupler is a 4-port waveguide junction consisting of a primary waveguide and a secondary waveguide. There are two small holes, which will be common to those two waveguides.

The Balanced Duplexer consists of two TR tubes. The configuration of Balanced Duplexer for transmission purpose is shown in the following figure.

The signal, which is produced by the transmitter has to reach the Antenna for the Antenna to transmit that signal during transmission time. The solid lines with arrow marks shown in the above figure represent how the signal reaches Antenna from transmitter.

The dotted lines with arrow marks shown in the above figure represent the signal, which is leaked from the Dual TR tubes; this will reach only the matched load. So, no signal has been reached to the receiver.

The configuration of Balanced Duplexer for reception purpose is shown in figure given below.

We know that Antenna receives the signal during reception time. The signal which is received by the Antenna has to reach the receiver. The solid lines with arrow marks shown in the above figure represent how the signal is reaching the receiver from Antenna. In this case, Dual TR tubes pass the signal from the first section of waveguide to the next section of waveguide.

The Balanced Duplexer has high power handling capability and high bandwidth when compared to Branch-type Duplexer.

Circulator as Duplexer

We know that the functionality of the circulator is that if we apply an input to a port, then it will be produced at the port, which is adjacent to it in the clockwise direction. There is no output at the remaining ports of the circulator.

So, consider a 4-port circulator and connect the transmitter, Antenna, receiver and matched load to port1, port2, port3 and port4 respectively. Now, let us understand how the 4-port circulator works as Duplexer.

The signal, which is produced by the transmitter has to reach the Antenna for the Antenna will transmit that signal during transmission time. This purpose will be achieved when the transmitter generates a signal at port1.

The signal, which is received by the Antenna has to reach the receiver during reception time. This purpose will be achieved when the Antenna present at port2 receives an external signal.

The following figure shows the block diagram of circulator as Duplexer −

The above figure consists of a 4-port circulator — Transmitter, Antenna and the matched load is connected to port1, port2 and port4 of circulator respectively as discussed in the beginning of the section.

The receiver is not directly connected to port3. Instead, the blocks corresponding to the passive TR limiter are placed between port3 of circulator and receiver. The blocks, TR tube & Diode limiter are the blocks corresponding to passive TR limiter.

Actually, the circulator itself acts as Duplexer. It does not require any additional blocks. However, it will not give any kind of protection to the receiver. Hence, the blocks corresponding to passive TR limiter are used in order to provide the protection to the receiver.

Radar Systems - Phased Array Antennas

A single Antenna can radiate certain amount of power in a particular direction. Obviously, the amount of radiation power will be increased when we use group of Antennas together. The group of Antennas is called Antenna array.

An Antenna array is a radiating system comprising radiators and elements. Each of this radiator has its own induction field. The elements are placed so closely that each one lies in the neighbouring one’s induction field. Therefore, the radiation pattern produced by them, would be the vector sum of the individual ones.

The Antennas radiate individually and while in an array, the radiation of all the elements sum up, to form the radiation beam, which has high gain, high directivity and better performance, with minimum losses.

An Antenna array is said to be Phased Antenna array if the shape and direction of the radiation pattern depends on the relative phases and amplitudes of the currents present at each Antenna of that array.

Radiation Pattern

Let us consider ‘n’ isotropic radiation elements, which when combined form an array. The figure given below will help you understand the same. Let the spacing between the successive elements be ‘d’ units.

As shown in the figure, all the radiation elements receive the same incoming signal. So, each element produces an equal output voltage of $sin \left ( \omega t \right)$. However, there will be an equal phase difference $\Psi$ between successive elements. Mathematically, it can be written as −

$$\Psi=\frac{2\pi d\sin\theta }{\lambda }\:\:\:\:\:Equation\:1$$

Where,

$\theta$ is the angle at which the incoming signal is incident on each radiation element.

Mathematically, we can write the expressions for output voltages of ‘n’ radiation elements individually as

$$E_1=\sin\left [ \omega t \right]$$

$$E_2=\sin\left [\omega t+\Psi\right]$$

$$E_3=\sin\left [\omega t+2\Psi\right]$$

$$.$$

$$.$$

$$.$$

$$E_n=\sin\left [\omega t+\left (N-1\right )\Psi\right]$$

Where,

$E_1, E_2, E_3, …, E_n$ are the output voltages of first, second, third, …, n^th radiation elements respectively.

$\omega$ is the angular frequency of the signal.

We will get the overall output voltage $E_a$ of the array by adding the output voltages of each element present in that array, since all those radiation elements are connected in linear array. Mathematically, it can be represented as −

$$E_a=E_1+E_2+E_3+ …+E_n \:\:\:Equation\:2$$

Substitute, the values of $E_1, E_2, E_3, …, E_n$ in Equation 2.

$$E_a=\sin\left [ \omega t \right]+\sin\left [\omega t+\Psi\right ]+\sin\left [\omega t+2\Psi\right ]+\sin\left [\omega t+\left (n-1\right )\Psi\right]$$

$$\Rightarrow E_a=\sin\left [\omega t+\frac{(n-1)\Psi)}{2}\right ]\frac{\sin\left [\frac{n\Psi}{2}\right]}{\sin\left [\frac{\Psi}{2}\right ]}\:\:\:\:\:Equation\:3$$

In Equation 3, there are two terms. From first term, we can observe that the overall output voltage $E_a$ is a sine wave having an angular frequency $\omega$. But, it is having a phase shift of $\left (n−1\right )\Psi/2$. The second term of Equation 3 is an amplitude factor.

The magnitude of Equation 3 will be

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\Psi}{2}\right ]}{\sin\left [\frac{\Psi}{2}\right]} \right |\:\:\:\:\:Equation\:4$$

We will get the following equation by substituting Equation 1 in Equation 4.

$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right]}{\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]} \right |\:\:\:\:\:Equation\:5$$

Equation 5 is called field intensity pattern. The field intensity pattern will have the values of zeros when the numerator of Equation 5 is zero

$$\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{n\pi d\sin\theta}{\lambda}=\pm m\pi$$

$$\Rightarrow nd\sin\theta=\pm m\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{m\lambda}{nd}$$

Where,

$m$ is an integer and it is equal to 1, 2, 3 and so on.

We can find the maximum values of field intensity pattern by using L-Hospital rule when both numerator and denominator of Equation 5 are equal to zero. We can observe that if the denominator of Equation 5 becomes zero, then the numerator of Equation 5 also becomes zero.

Now, let us get the condition for which the denominator of Equation 5 becomes zero.

$$\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]=0$$

$$\Rightarrow \frac{\pi d\sin\theta}{\lambda}=\pm p\pi$$

$$\Rightarrow d\sin\theta=\pm p\lambda$$

$$\Rightarrow \sin\theta=\pm \frac{p\lambda}{d}$$

Where,

$p$ is an integer and it is equal to 0, 1, 2, 3 and so on.

If we consider $p$ as zero, then we will get the value of $\sin\theta$ as zero. For this case, we will get the maximum value of field intensity pattern corresponding to the main lobe. We will get the maximum values of field intensity pattern corresponding to side lobes, when we consider other values of $p$.

The radiation pattern’s direction of phased array can be steered by varying the relative phases of the current present at each Antenna. This is the advantage of electronic scanning phased array.