Bir Çemberin Kesirli Bölümü
Tam veya tam bir daire 1 olarak alınır ve dairelerin bölümleri kesir olarak temsil edilir. Örneğin, bir daire 8 eşit parçaya bölünürse, parçaların her biri 1/8 kesri temsil eder. Böyle bir dairenin üç parçası 3/8 ve üzeri temsil eder.
Burada, bir daire içindeki belirli bölümleri temsil eden kesirlerin verildiği ve çemberin kalan bilinmeyen bölümünü temsil eden kesri bulmamız gereken bir tür problemle uğraşıyoruz. Bu tür problemleri çözmek için, kesirli kısımları temsil eden kesirleri topluyoruz ve ardından toplamı 1'den, tüm çemberden çıkarıyoruz. Sonuç, çemberin bilinmeyen kesirli kısmını temsil eden kesri verir.
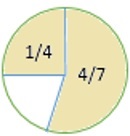
Çemberin ne kadarı gölgesiz? Cevabınızı en basit şekilde kesir olarak yazın.
Çözüm
Step 1:
Önce şeklin hangi kısmının gölgeli olduğunu buluyoruz.
$ \ frac {1} {4} $ + $ \ frac {4} {7} $ = $ \ frac {7} {28} $ + $ \ frac {16} {28} $ = $ \ frac {(7 +16)} {28} $ = $ \ frac {23} {28} $
Step 2:
Şeklin gölgesiz olan kısmını bulmak için elde ettiğimiz sonucu ( $ \ frac {23} {28} $ ) 1'den çıkarıyoruz .
1 - $ \ frac {23} {28} $ = $ \ frac {28} {28} $ - $ \ frac {23} {28} $ = $ \ frac {(28−23} {28} $ = $ \ frac {5} {28} $
Yani, gölgesiz rakamın oranı $ \ frac {5} {28} $ ' dır .
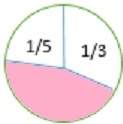
Çemberin ne kadarı gölgeli? Cevabınızı en basit şekilde kesir olarak yazın.
Çözüm
Step 1:
İlk önce rakamın ne kadarının gölgesiz olduğunu buluyoruz.
$ \ frac {1} {5} $ + $ \ frac {1} {3} $ = $ \ frac {3} {15} $ + $ \ frac {5} {15} $ = $ \ frac {(3 +5)} {15} $ = $ \ frac {8} {15} $
Step 2:
Şeklin gölgesiz olan kısmını bulmak için elde ettiğimiz sonucu ( $ \ frac {8} {15} $ ) 1'den çıkarıyoruz .
1 - $ \ frac {8} {15} $ = $ \ frac {15} {15} $ - $ \ frac {8} {15} $ = $ \ frac {(15−8)} {15} $ = $ \ frac {7} {15} $
Yani, gölgeli rakamın oranı $ \ frac {7} {15} $ ' dır .