Büyük Veri Analitiği - Hızlı Kılavuz
Birinin uğraşması gereken veri hacmi, geçtiğimiz on yılda hayal bile edilemeyecek seviyelere ulaştı ve aynı zamanda, veri depolamanın fiyatı sistematik olarak düştü. Özel şirketler ve araştırma kurumları, kullanıcılarının etkileşimleri, iş dünyası, sosyal medya ve ayrıca cep telefonları ve otomobiller gibi cihazlardan gelen sensörlerle ilgili terabaytlarca veri toplar. Bu çağın zorluğu, bu veri denizini anlamlandırmaktır. Bu neredebig data analytics resme geliyor.
Büyük Veri Analitiği, büyük ölçüde farklı kaynaklardan veri toplamayı, analistler tarafından tüketilebilecek şekilde işlemeyi ve nihayetinde organizasyon işi için yararlı veri ürünleri sunmayı içerir.

Farklı kaynaklardan alınan büyük miktarda yapılandırılmamış ham veriyi, kuruluşlar için yararlı bir veri ürününe dönüştürme süreci, Büyük Veri Analitiğinin temelini oluşturur.
Geleneksel Veri Madenciliği Yaşam Döngüsü
Bir kuruluşun ihtiyaç duyduğu işi organize etmek ve Büyük Veriden net içgörüler sağlamak için bir çerçeve sağlamak için, bunu farklı aşamaları olan bir döngü olarak düşünmek yararlıdır. Hiçbir şekilde doğrusal değildir, yani tüm aşamalar birbiriyle ilişkilidir. Bu döngü, daha geleneksel veri madenciliği döngüsü ile yüzeysel benzerliklere sahiptir.CRISP methodology.
CRISP-DM Metodolojisi
CRISP-DM methodologyVeri Madenciliği için Sektörler Arası Standart Süreç anlamına gelen bu, veri madenciliği uzmanlarının geleneksel BI veri madenciliğindeki sorunları çözmek için kullandıkları yaygın olarak kullanılan yaklaşımları açıklayan bir döngüdür. Halen geleneksel BI veri madenciliği ekiplerinde kullanılmaktadır.
Aşağıdaki resme bir göz atın. CRISP-DM metodolojisi tarafından tanımlanan döngünün ana aşamalarını ve bunların birbiriyle nasıl ilişkili olduğunu gösterir.
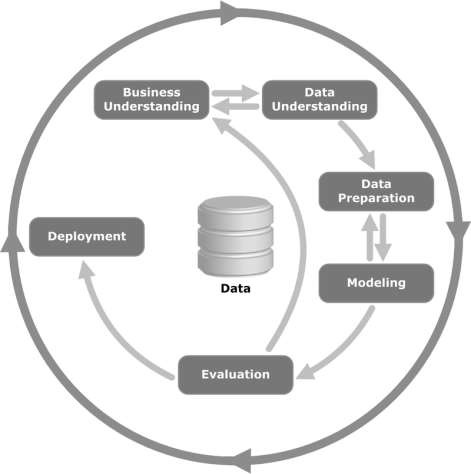
CRISP-DM 1996 yılında tasarlandı ve ertesi yıl, ESPRIT finansman girişimi kapsamında bir Avrupa Birliği projesi olarak başladı. Proje beş şirket tarafından yönetildi: SPSS, Teradata, Daimler AG, NCR Corporation ve OHRA (bir sigorta şirketi). Proje nihayet SPSS'ye dahil edildi. Metodoloji, bir veri madenciliği projesinin nasıl belirtilmesi gerektiği konusunda son derece ayrıntılıdır.
Şimdi CRISP-DM yaşam döngüsünün her bir aşaması hakkında biraz daha bilgi edinelim -
Business Understanding- Bu ilk aşama, proje hedeflerini ve gereksinimlerini bir iş perspektifinden anlamaya ve ardından bu bilgiyi bir veri madenciliği problem tanımına dönüştürmeye odaklanır. Hedeflere ulaşmak için bir ön plan tasarlanır. Bir karar modeli, özellikle Karar Modeli ve Notasyon standardı kullanılarak oluşturulan bir model kullanılabilir.
Data Understanding - Verileri anlama aşaması, ilk veri toplama ile başlar ve verilere aşina olmak, veri kalitesi sorunlarını belirlemek, verilerle ilgili ilk içgörüleri keşfetmek veya gizli bilgiler için hipotezler oluşturmak için ilginç alt kümeleri tespit etmek için faaliyetlerle devam eder.
Data Preparation- Veri hazırlama aşaması, ilk ham verilerden nihai veri setini (modelleme araçlarına / araçlarına beslenecek veriler) oluşturmak için tüm faaliyetleri kapsar. Veri hazırlama görevleri, önceden belirlenmiş herhangi bir sırayla değil, muhtemelen birden çok kez gerçekleştirilecektir. Görevler arasında tablo, kayıt ve öznitelik seçimi ile modelleme araçları için verilerin dönüştürülmesi ve temizlenmesi yer alır.
Modeling- Bu aşamada, çeşitli modelleme teknikleri seçilir ve uygulanır ve parametreleri optimum değerlere kalibre edilir. Tipik olarak, aynı veri madenciliği problem türü için birkaç teknik vardır. Bazı tekniklerin veri biçimiyle ilgili özel gereksinimleri vardır. Bu nedenle, genellikle veri hazırlama aşamasına geri dönmek gerekir.
Evaluation- Projenin bu aşamasında, veri analizi açısından yüksek kalitede görünen bir model (veya modeller) oluşturdunuz. Modelin nihai dağıtımına geçmeden önce, modeli kapsamlı bir şekilde değerlendirmek ve iş hedeflerine uygun şekilde ulaştığından emin olmak için modeli oluşturmak için yürütülen adımları gözden geçirmek önemlidir.
Temel amaçlardan biri, yeterince dikkate alınmamış bazı önemli ticari meselelerin olup olmadığını belirlemektir. Bu aşamanın sonunda, veri madenciliği sonuçlarının kullanımına ilişkin bir karara varılmalıdır.
Deployment- Modelin oluşturulması genellikle projenin sonu değildir. Modelin amacı verilere ilişkin bilgiyi artırmak olsa bile, kazanılan bilginin müşteriye yararlı olacak şekilde organize edilmesi ve sunulması gerekecektir.
Gereksinimlere bağlı olarak, dağıtım aşaması bir rapor oluşturmak kadar basit veya tekrarlanabilir bir veri puanlaması (örneğin, bölüm tahsisi) veya veri madenciliği sürecini uygulamak kadar karmaşık olabilir.
Çoğu durumda, dağıtım adımlarını gerçekleştirecek olan veri analisti değil müşteri olacaktır. Analist modeli devreye alsa bile, müşterinin oluşturulan modellerden fiilen yararlanmak için gerçekleştirilmesi gereken eylemleri önceden anlaması önemlidir.
SEMMA Metodolojisi
SEMMA, SAS tarafından veri madenciliği modellemesi için geliştirilen başka bir metodolojidir. Anlamına gelirSbol, Explore, Modify, Model ve Asses. İşte aşamalarının kısa bir açıklaması -
Sample- Süreç, veri örnekleme ile başlar, örneğin, modelleme için veri setini seçme. Veri kümesi, alınacak yeterli bilgiyi içerecek kadar büyük, ancak verimli bir şekilde kullanılacak kadar küçük olmalıdır. Bu aşama aynı zamanda veri bölümleme ile de ilgilenir.
Explore - Bu aşama, veri görselleştirme yardımıyla değişkenler arasındaki beklenen ve beklenmeyen ilişkileri ve anormallikleri keşfederek verilerin anlaşılmasını kapsar.
Modify - Değiştirme aşaması, veri modellemeye hazırlanırken değişkenleri seçmek, oluşturmak ve dönüştürmek için yöntemler içerir.
Model - Model aşamasında, muhtemelen istenen sonucu sağlayacak modeller oluşturmak için hazırlanan değişkenler üzerinde çeşitli modelleme (veri madenciliği) tekniklerinin uygulanmasına odaklanılır.
Assess - Modelleme sonuçlarının değerlendirilmesi, oluşturulan modellerin güvenilirliğini ve kullanışlılığını gösterir.
CRISM-DM ve SEMMA arasındaki temel fark, SEMMA'nın modelleme yönüne odaklanmasıdır, CRISP-DM ise çözülecek iş problemini anlama, veriyi anlama ve ön işleme gibi modellemeden önce döngünün aşamalarına daha fazla önem verir. girdi olarak kullanılır, örneğin makine öğrenimi algoritmaları.
Büyük Veri Yaşam Döngüsü
Günümüzün büyük veri bağlamında, önceki yaklaşımlar ya eksiktir ya da yetersizdir. Örneğin, SEMMA metodolojisi veri toplamayı ve farklı veri kaynaklarının ön işlemesini tamamen göz ardı eder. Bu aşamalar normalde başarılı bir büyük veri projesindeki işin çoğunu oluşturur.
Bir büyük veri analitiği döngüsü aşağıdaki aşamada tanımlanabilir -
- İş Problemi Tanımı
- Research
- İnsan Kaynakları Değerlendirmesi
- Veri toplama
- Veri Parçalama
- Veri depolama
- Keşfedici Veri Analizi
- Modelleme ve Değerlendirme için Veri Hazırlama
- Modeling
- Implementation
Bu bölümde, büyük veri yaşam döngüsünün bu aşamalarının her birine biraz ışık tutacağız.
İş Problemi Tanımı
Bu, geleneksel iş zekası ve büyük veri analitiği yaşam döngüsünde ortak bir noktadır. Normalde, problemi tanımlamak ve bir organizasyon için ne kadar potansiyel kazancı olabileceğini doğru bir şekilde değerlendirmek büyük veri projesinin önemsiz olmayan bir aşamasıdır. Bundan bahsedilmesi açık gibi görünüyor, ancak projenin beklenen kazanımları ve maliyetlerinin neler olduğu değerlendirilmelidir.
Araştırma
Aynı durumda diğer şirketlerin neler yaptığını analiz edin. Bu, diğer çözümleri şirketinizin sahip olduğu kaynaklara ve gereksinimlere uyarlamayı gerektirse de, şirketiniz için makul olan çözümleri aramayı içerir. Bu aşamada, gelecek aşamalar için bir metodoloji tanımlanmalıdır.
İnsan Kaynakları Değerlendirmesi
Sorun tanımlandıktan sonra, mevcut personelin projeyi başarıyla tamamlayıp tamamlamadığını analiz etmeye devam etmek mantıklıdır. Geleneksel iş zekası ekipleri tüm aşamalara en uygun çözümü sunamayabilir, bu nedenle projenin bir bölümünü dış kaynaklara yaptırma veya daha fazla kişiyi işe alma ihtiyacı varsa, projeye başlamadan önce dikkate alınmalıdır.
Veri toplama
Bu bölüm, büyük veri yaşam döngüsünün anahtarıdır; ortaya çıkan veri ürününü sunmak için hangi tip profillerin gerekli olacağını tanımlar. Veri toplama, sürecin önemsiz olmayan bir adımıdır; normalde farklı kaynaklardan yapılandırılmamış verilerin toplanmasını içerir. Bir örnek vermek gerekirse, bir web sitesinden yorumları almak için bir tarayıcı yazmayı içerebilir. Bu, belki de normalde tamamlanması önemli miktarda zaman gerektiren farklı dillerde metinle uğraşmayı içerir.
Veri Parçalama
Veriler örneğin web'den alındıktan sonra, kullanımı kolay bir formatta depolanması gerekir. İnceleme örnekleriyle devam etmek için, verilerin, her birinin farklı bir veri görüntüsüne sahip olduğu farklı sitelerden alındığını varsayalım.
Bir veri kaynağının yıldızlarla derecelendirme açısından yorumlar verdiğini varsayalım, bu nedenle bunu yanıt değişkeni için bir eşleme olarak okumak mümkündür. y ∈ {1, 2, 3, 4, 5}. Başka bir veri kaynağı, biri yukarı oylama, diğeri aşağı oylama için olmak üzere iki ok sistemini kullanarak incelemeler verir. Bu, formun bir yanıt değişkeni anlamına geliry ∈ {positive, negative}.
Her iki veri kaynağını birleştirmek için, bu iki yanıt temsilini eşdeğer kılmak için bir karar verilmesi gerekir. Bu, bir yıldızı negatif ve beş yıldızı pozitif olarak kabul ederek, birinci veri kaynağı yanıt temsilini ikinci forma dönüştürmeyi içerebilir. Bu süreç genellikle iyi kalitede teslim edilmek için büyük bir zaman ayırmayı gerektirir.
Veri depolama
Veriler işlendikten sonra bazen bir veritabanında saklanması gerekir. Büyük veri teknolojileri bu konuda pek çok alternatif sunuyor. En yaygın alternatif, kullanıcılara HIVE Sorgu Dili olarak bilinen sınırlı bir SQL sürümü sağlayan depolama için Hadoop Dosya Sistemini kullanmaktır. Bu, çoğu analitik görevinin, kullanıcı perspektifinden geleneksel BI veri ambarlarında yapılacağı gibi benzer şekillerde yapılmasına olanak tanır. Dikkate alınacak diğer depolama seçenekleri MongoDB, Redis ve SPARK'tır.
Döngünün bu aşaması, farklı mimarileri uygulama yetenekleri açısından insan kaynakları bilgisi ile ilgilidir. Geleneksel veri ambarlarının değiştirilmiş sürümleri hala büyük ölçekli uygulamalarda kullanılmaktadır. Örneğin, teradata ve IBM, terabaytlarca veriyi işleyebilen SQL veritabanları sunar; postgreSQL ve MySQL gibi açık kaynaklı çözümler, büyük ölçekli uygulamalar için hala kullanılmaktadır.
İstemci tarafından arka planda farklı depoların nasıl çalıştığı konusunda farklılıklar olsa da çoğu çözüm bir SQL API sağlar. Bu nedenle, SQL'i iyi anlamak, büyük veri analitiği için hala sahip olunması gereken temel bir beceridir.
Bu aşama a priori en önemli konu gibi görünüyor, pratikte bu doğru değil. Hatta gerekli bir aşama bile değil. Gerçek zamanlı verilerle çalışacak bir büyük veri çözümü uygulamak mümkündür, bu nedenle bu durumda, modeli geliştirmek ve ardından gerçek zamanlı olarak uygulamak için yalnızca veri toplamamız gerekir. Dolayısıyla, verilerin resmi olarak saklanmasına hiç gerek kalmaz.
Keşfedici Veri Analizi
Veriler temizlendikten ve içgörüler alınabilecek şekilde depolandıktan sonra, veri araştırma aşaması zorunludur. Bu aşamanın amacı, verileri anlamaktır, bu normalde istatistiksel tekniklerle ve ayrıca verilerin grafiğini çizerek yapılır. Bu, problem tanımının mantıklı mı yoksa uygulanabilir mi olduğunu değerlendirmek için iyi bir aşamadır.
Modelleme ve Değerlendirme için Veri Hazırlama
Bu aşama, önceden alınan temizlenmiş verilerin yeniden şekillendirilmesini ve eksik değerlerin atanması, aykırı değer tespiti, normalleştirme, özellik çıkarma ve özellik seçimi için istatistiksel ön işlemeyi kullanmayı içerir.
Modelleme
Önceki aşama, örneğin tahmine dayalı bir model gibi eğitim ve test için birkaç veri kümesi üretmiş olmalıdır. Bu aşama, farklı modelleri denemeyi ve eldeki iş problemini çözmeyi dört gözle beklemeyi içerir. Uygulamada, normalde modelin işletmeye biraz içgörü vermesi istenir. Son olarak, en iyi model veya modellerin kombinasyonu, dışarıda bırakılmış bir veri kümesindeki performansı değerlendirilerek seçilir.
Uygulama
Bu aşamada geliştirilen veri ürünü firmanın veri hattında hayata geçirilir. Bu, performansını izlemek için veri ürünü çalışırken bir doğrulama şeması oluşturmayı içerir. Örneğin, bir tahmine dayalı modelin uygulanması durumunda, bu aşama, modelin yeni verilere uygulanmasını ve yanıt mevcut olduğunda modeli değerlendirmeyi içerir.
Metodoloji açısından, büyük veri analitiği, deneysel tasarımın geleneksel istatistiksel yaklaşımından önemli ölçüde farklıdır. Analitik verilerle başlar. Normalde verileri bir yanıtı açıklayacak şekilde modelleriz. Bu yaklaşımın amacı, yanıt davranışını tahmin etmek veya girdi değişkenlerinin bir yanıtla nasıl ilişkili olduğunu anlamaktır. Normalde istatistiksel deneysel tasarımlarda bir deney geliştirilir ve sonuç olarak veriler alınır. Bu, bağımsızlık, normallik ve rastgeleleştirme gibi belirli varsayımların geçerli olduğu istatistiksel bir model tarafından kullanılabilecek bir şekilde veri üretmeye izin verir.
Büyük veri analitiğinde verilerle karşımıza çıkıyor. Favori istatistiksel modelimizi karşılayan bir deney tasarlayamayız. Büyük ölçekli analitik uygulamalarında, yalnızca verileri temizlemek için büyük miktarda çalışma (normalde çabanın% 80'i) gerekir, bu nedenle bir makine öğrenimi modeli tarafından kullanılabilir.
Gerçek büyük ölçekli uygulamalarda izleyeceğimiz benzersiz bir metodolojimiz yok. Normalde iş problemi tanımlandıktan sonra, kullanılacak metodolojiyi tasarlamak için bir araştırma aşamasına ihtiyaç vardır. Bununla birlikte, genel yönergelerin belirtilmesi ve hemen hemen tüm problemler için geçerli olması önemlidir.
Büyük veri analitiğindeki en önemli görevlerden biri statistical modeling, denetimli ve denetimsiz sınıflandırma veya regresyon problemleri anlamına gelir. Modelleme için uygun olan veriler temizlendikten ve ön işlemden geçirildikten sonra, makul kayıp ölçüleriyle farklı modellerin değerlendirilmesine özen gösterilmeli ve ardından model uygulandıktan sonra daha fazla değerlendirme ve sonuçlar raporlanmalıdır. Tahmine dayalı modellemede sık karşılaşılan bir tuzak, modeli uygulamak ve performansını asla ölçmemektir.
Büyük veri yaşam döngüsünde belirtildiği gibi, bir büyük veri ürünü geliştirmenin sonucu olan veri ürünleri çoğu durumda aşağıdakilerden bazılarıdır:
Machine learning implementation - Bu bir sınıflandırma algoritması, bir regresyon modeli veya bir segmentasyon modeli olabilir.
Recommender system - Amaç, kullanıcı davranışına göre seçimler öneren bir sistem geliştirmektir. Netflix bu veri ürününün karakteristik bir örneğidir, burada kullanıcıların derecelendirmelerine göre başka filmler önerilir.
Dashboard- İşletme normalde birleştirilmiş verileri görselleştirmek için araçlara ihtiyaç duyar. Gösterge panosu, bu verileri erişilebilir kılmak için grafiksel bir mekanizmadır.
Ad-Hoc analysis - Normalde iş alanlarında, verilerle anlık analiz yaparak yanıtlanabilecek sorular, hipotezler veya efsaneler vardır.
Büyük organizasyonlarda, bir büyük veri projesini başarılı bir şekilde geliştirmek için, projeyi yedekleyen yönetime ihtiyaç vardır. Bu normalde projenin ticari avantajlarını göstermenin bir yolunu bulmayı içerir. Bir proje için sponsor bulma sorununa benzersiz bir çözümümüz yok, ancak aşağıda birkaç yönerge verilmiştir -
Sizi ilgilendiren projeye benzer diğer projelerin sponsorlarının kim ve nerede olduğunu kontrol edin.
Kilit yönetim pozisyonlarında kişisel bağlantılara sahip olmak yardımcı olur, böylece proje ümit vaat ediyorsa herhangi bir temas tetiklenebilir.
Projenizden kimler faydalanır? Proje yoluna girdiğinde müşteriniz kim olur?
Basit, net ve son derece heyecan verici bir teklif geliştirin ve bunu kuruluşunuzdaki önemli oyuncularla paylaşın.
Bir proje için sponsor bulmanın en iyi yolu, sorunu ve uygulandığında ortaya çıkan veri ürününün ne olacağını anlamaktır. Bu anlayış, büyük veri projesinin önemi konusunda yönetimi ikna etmede bir avantaj sağlayacaktır.
Bir veri analisti, SQL kullanarak geleneksel veri ambarlarından veri çıkarma ve analiz etme deneyimine sahip, raporlama odaklı profile sahiptir. Görevleri normalde ya veri depolama tarafında ya da genel iş sonuçlarını rapor etmede. Veri ambarlama hiçbir şekilde basit değildir, sadece bir veri bilimcinin yaptığından farklıdır.
Birçok kuruluş, pazarda yetkin veri bilimcileri bulmak için büyük çaba harcıyor. Bununla birlikte, potansiyel veri analistlerini seçmek ve onlara bir veri bilimcisi olmak için gerekli becerileri öğretmek iyi bir fikirdir. Bu hiçbir şekilde önemsiz bir görev değildir ve normal olarak kantitatif bir alanda yüksek lisans yapan kişiyi içerir, ancak kesinlikle uygulanabilir bir seçenektir. Yetkin bir veri analistinin sahip olması gereken temel beceriler aşağıda listelenmiştir -
- İş anlayışı
- SQL programlama
- Rapor tasarımı ve uygulaması
- Gösterge tablosu geliştirme
Bir veri bilimcisinin rolü normalde tahmine dayalı modelleme, bölümleme algoritmaları geliştirme, tavsiye sistemleri, A / B testi çerçeveleri ve genellikle ham yapılandırılmamış verilerle çalışma gibi görevlerle ilişkilidir.
Çalışmalarının doğası derin bir matematik, uygulamalı istatistik ve programlama anlayışı gerektirir. Bir veri analisti ile veri bilimcisi arasında ortak olan birkaç beceri vardır, örneğin, veritabanlarını sorgulama yeteneği. Her ikisi de verileri analiz eder, ancak bir veri bilimcisinin kararı bir organizasyonda daha büyük bir etkiye sahip olabilir.
İşte bir veri bilimcinin normalde sahip olması gereken bir dizi beceri:
- R, Python, SAS, SPSS veya Julia gibi istatistiksel bir pakette programlama
- Farklı kaynaklardan verileri temizleyebilir, çıkarabilir ve keşfedebilir
- İstatistiksel modellerin araştırılması, tasarımı ve uygulanması
- Derin istatistiksel, matematiksel ve bilgisayar bilimi bilgisi
Büyük veri analitiğinde, insanlar normalde bir veri bilimcisinin rolünü bir veri mimarı rolüyle karıştırır. Gerçekte, fark oldukça basittir. Bir veri mimarı, verilerin depolanacağı araçları ve mimariyi tanımlar, oysa bir veri bilimcisi bu mimariyi kullanır. Elbette, bir veri bilimcisi, özel projeler için gerekirse yeni araçlar kurabilmelidir, ancak altyapı tanımı ve tasarımı, görevinin bir parçası olmamalıdır.
Bu eğitim aracılığıyla bir proje geliştireceğiz. Bu eğitimdeki sonraki her bölüm, mini proje bölümündeki daha büyük projenin bir bölümünü ele almaktadır. Bunun, gerçek dünyadaki bir soruna maruz kalmayı sağlayacak uygulamalı bir eğitim bölümü olduğu düşünülmektedir. Bu durumda, projenin problem tanımıyla başlayacağız.
Proje Açıklaması
Bu projenin amacı, özgeçmiş (CV) metinlerini girdi olarak kullanan kişilerin saatlik maaşlarını tahmin etmek için bir makine öğrenimi modeli geliştirmek olacaktır.
Yukarıda tanımlanan çerçeveyi kullanarak problemi tanımlamak basittir. X = {x 1 , x 2 ,…, x n } 'yi kullanıcıların CV'leri olarak tanımlayabiliriz , burada her özellik mümkün olan en basit şekilde bu kelimenin görünme miktarı olabilir. O zaman cevap gerçek değerlidir, bireylerin saatlik maaşını dolar cinsinden tahmin etmeye çalışıyoruz.
Bu iki husus, sunulan sorunun denetimli bir regresyon algoritması ile çözülebileceği sonucuna varmak için yeterlidir.
Problem tanımı
Problem Definitionbüyük veri analitiği ardışık düzeninde muhtemelen en karmaşık ve en çok ihmal edilen aşamalardan biridir. Bir veri ürününün çözeceği problemi tanımlamak için deneyim zorunludur. Çoğu veri bilimcisi adayının bu aşamada çok az deneyimi vardır veya hiç yoktur.
Çoğu büyük veri sorunu aşağıdaki şekillerde kategorize edilebilir:
- Denetimli sınıflandırma
- Denetimli regresyon
- Denetimsiz öğrenme
- Sıralamayı öğrenmek
Şimdi bu dört kavram hakkında daha fazla bilgi edinelim.
Denetimli Sınıflandırma
X = {x 1 , x 2 , ..., x n } özelliklerinin bir matrisi verildiğinde , y = {c 1 , c 2 , ..., c n } olarak tanımlanan farklı sınıfları tahmin etmek için bir M modeli geliştiririz . Örneğin: Bir sigorta şirketindeki müşterilerin işlem verileri göz önüne alındığında, bir müşterinin işi bırakıp bırakmayacağını tahmin edecek bir model geliştirmek mümkündür. İkincisi, iki sınıfın veya hedef değişkenlerin olduğu ikili bir sınıflandırma problemidir: çalkalama ve çalkalama değil.
Diğer problemler birden fazla sınıfı tahmin etmeyi içerir, rakam tanıma yapmak ilgimizi çekebilir, bu nedenle yanıt vektörü şu şekilde tanımlanır: y = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} en son teknoloji modeli evrişimli sinir ağı olacaktır ve özelliklerin matrisi görüntünün pikselleri olarak tanımlanacaktır.
Denetimli Regresyon
Bu durumda, problem tanımı önceki örneğe oldukça benzerdir; fark, yanıta bağlıdır. Bir regresyon probleminde, y ∈ ℜ yanıtı, bu yanıtın gerçek değerli olduğu anlamına gelir. Örneğin, özgeçmişlerinin külliyatı verilen bireylerin saatlik maaşlarını tahmin etmek için bir model geliştirebiliriz.
Denetimsiz Öğrenme
Yönetim genellikle yeni anlayışlara susamıştır. Segmentasyon modelleri, pazarlama departmanının farklı segmentler için ürünler geliştirmesi için bu içgörüyü sağlayabilir. Algoritmaları düşünmek yerine bir segmentasyon modeli geliştirmek için iyi bir yaklaşım, istenen segmentasyonla ilgili özellikleri seçmektir.
Örneğin, bir telekomünikasyon şirketinde, müşterileri cep telefonu kullanımlarına göre bölümlere ayırmak ilginçtir. Bu, segmentasyon hedefiyle hiçbir ilgisi olmayan özellikleri göz ardı etmeyi ve yalnızca yapanları dahil etmeyi içerir. Bu durumda, bu, bir ayda kullanılan SMS sayısı, gelen ve giden dakika sayısı vb. Gibi özelliklerin seçilmesi olacaktır.
Sıralamayı Öğrenmek
Bu problem bir regresyon problemi olarak düşünülebilir, ancak kendine has özellikleri vardır ve ayrı bir muameleyi hak eder. Sorun, bir sorguya en uygun sıralamayı bulmaya çalıştığımız bir dizi belgeyi içerir. Denetimli bir öğrenme algoritması geliştirmek için, bir sorgu verildiğinde bir siparişin ne kadar alakalı olduğunu etiketlemek gerekir.
Denetimli bir öğrenme algoritması geliştirmek için eğitim verilerinin etiketlenmesi gerektiğine dikkat etmek önemlidir. Bu, örneğin bir görüntüdeki basamakları tanıyan bir modeli eğitmek için, önemli miktarda örneği elle etiketlememiz gerektiği anlamına gelir. Bu işlemi hızlandırabilen ve bu görev için yaygın olarak kullanılan amazon mekanik türk gibi web servisleri vardır. Öğrenme algoritmalarının daha fazla veri sağlandığında performanslarını artırdığı kanıtlanmıştır, bu nedenle denetimli öğrenmede makul miktarda örnek etiketlemek pratik olarak zorunludur.
Veri toplama, Büyük Veri döngüsünde en önemli rolü oynar. İnternet, çeşitli konular için neredeyse sınırsız veri kaynağı sağlar. Bu alanın önemi, işin türüne bağlıdır, ancak geleneksel endüstriler çeşitli dış veri kaynakları elde edebilir ve bunları işlem verileriyle birleştirebilir.
Örneğin, restoranlar öneren bir sistem kurmak istediğimizi varsayalım. İlk adım, bu durumda, farklı web sitelerinden restoran incelemeleri hakkında veri toplamak ve bunları bir veritabanında saklamak olacaktır. Ham metinle ilgilendiğimizden ve bunu analitik için kullanacağımızdan, modeli geliştirmek için verilerin nerede depolanacağı o kadar alakalı değildir. Bu, büyük veri ana teknolojileriyle çelişkili gelebilir, ancak bir büyük veri uygulamasını hayata geçirmek için, onu gerçek zamanlı olarak çalıştırmamız gerekiyor.
Twitter Mini Projesi
Sorun tanımlandıktan sonra, sonraki aşama verileri toplamaktır. Aşağıdaki mini proje fikri, web'den veri toplama ve bir makine öğrenimi modelinde kullanılmak üzere yapılandırmaya çalışmaktır. R programlama dilini kullanarak twitter dinlenme API'sinden bazı tweet'ler toplayacağız.
Öncelikle bir twitter hesabı oluşturun ve ardından sayfadaki talimatları izleyin. twitteRtwitter geliştirici hesabı oluşturmak için paket vinyet . Bu, bu talimatların bir özetidir -
Git https://twitter.com/apps/new ve oturum açın.
Temel bilgileri doldurduktan sonra, "Ayarlar" sekmesine gidin ve "Doğrudan mesajları Oku, Yaz ve Eriş" seçeneğini seçin.
Bunu yaptıktan sonra kaydet düğmesine tıkladığınızdan emin olun.
"Ayrıntılar" sekmesinde, tüketici anahtarınızı ve tüketici sırrınızı not edin
R oturumunuzda, API anahtarını ve API gizli değerlerini kullanacaksınız
Son olarak aşağıdaki komut dosyasını çalıştırın. Bu,twitteR paketi github üzerindeki deposundan.
install.packages(c("devtools", "rjson", "bit64", "httr"))
# Make sure to restart your R session at this point
library(devtools)
install_github("geoffjentry/twitteR")"Big Mac" dizesinin dahil olduğu verileri almak ve bu konuda hangi konuların öne çıktığını bulmakla ilgileniyoruz. Bunu yapmak için ilk adım, verileri twitter'dan toplamaktır. Twitter'dan gerekli verileri toplamak için R komut dosyamız aşağıdadır. Bu kod ayrıca bda / part1 / Collect_data / Collect_data_twitter.R dosyasında da mevcuttur.
rm(list = ls(all = TRUE)); gc() # Clears the global environment
library(twitteR)
Sys.setlocale(category = "LC_ALL", locale = "C")
### Replace the xxx’s with the values you got from the previous instructions
# consumer_key = "xxxxxxxxxxxxxxxxxxxx"
# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# Connect to twitter rest API
setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)
# Get tweets related to big mac
tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)
df <- twListToDF(tweets)
# Take a look at the data
head(df)
# Check which device is most used
sources <- sapply(tweets, function(x) x$getStatusSource())
sources <- gsub("</a>", "", sources)
sources <- strsplit(sources, ">")
sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))
source_table = table(sources)
source_table = source_table[source_table > 1]
freq = source_table[order(source_table, decreasing = T)]
as.data.frame(freq)
# Frequency
# Twitter for iPhone 71
# Twitter for Android 29
# Twitter Web Client 25
# recognia 20Veriler toplandıktan sonra, normalde farklı özelliklere sahip çeşitli veri kaynaklarımız olur. En acil adım, bu veri kaynaklarını homojen hale getirmek ve veri ürünümüzü geliştirmeye devam etmek olacaktır. Ancak, veri türüne bağlıdır. Verileri homojenleştirmenin pratik olup olmadığını kendimize sormalıyız.
Belki veri kaynakları tamamen farklıdır ve kaynaklar homojen hale getirilirse bilgi kaybı büyük olacaktır. Bu durumda alternatifler düşünebiliriz. Bir veri kaynağı bir regresyon modeli ve diğeri bir sınıflandırma modeli oluşturmama yardımcı olabilir mi? Bilgi kaybetmektense, bizim avantajımız olan heterojenlikle çalışmak mümkün mü? Bu kararları almak, analitiği ilginç ve zorlu kılan şeydir.
İnceleme durumunda, her veri kaynağı için bir dil olması mümkündür. Yine, iki seçeneğimiz var -
Homogenization- Farklı dilleri daha fazla veriye sahip olduğumuz dile çevirmeyi içerir. Çeviri hizmetlerinin kalitesi kabul edilebilir, ancak büyük miktarda veriyi bir API ile çevirmek istersek, maliyet önemli olacaktır. Bu görev için mevcut yazılım araçları vardır, ancak bu da maliyetli olacaktır.
Heterogenization- Her dil için bir çözüm geliştirmek mümkün müdür? Bir külliyatın dilini tespit etmek basit olduğundan, her dil için bir önerici geliştirebiliriz. Bu, her bir tavsiyenin mevcut dil miktarına göre ayarlanması açısından daha fazla çalışmayı gerektirecektir, ancak mevcut birkaç dilimiz varsa kesinlikle uygun bir seçenektir.
Twitter Mini Projesi
Mevcut durumda, konu modellemesini uygulamak için önce yapılandırılmamış verileri temizlememiz ve ardından bir veri matrisine dönüştürmemiz gerekiyor. Genel olarak, twitter'dan veri alırken, en azından veri temizleme işleminin ilk aşamasında kullanmak istemediğimiz birkaç karakter vardır.
Örneğin, tweetleri aldıktan sonra şu garip karakterleri alıyoruz: "<ed> <U + 00A0> <U + 00BD> <ed> <U + 00B8> <U + 008B>". Bunlar muhtemelen ifadelerdir, bu nedenle verileri temizlemek için aşağıdaki komut dosyasını kullanarak onları kaldıracağız. Bu kod ayrıca bda / part1 / Collect_data / Cleaning_data.R dosyasında da mevcuttur.
rm(list = ls(all = TRUE)); gc() # Clears the global environment
source('collect_data_twitter.R')
# Some tweets
head(df$text)
[1] "I’m not a big fan of turkey but baked Mac &
cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"
[2] "@Jayoh30 Like no special sauce on a big mac. HOW"
### We are interested in the text - Let’s clean it!
# We first convert the encoding of the text from latin1 to ASCII
df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))
# Create a function to clean tweets
clean.text <- function(tx) {
tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)
tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)
tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)
tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)
tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE) return(tx) } clean_tweets <- lapply(df$text, clean.text)
# Cleaned tweets
head(clean_tweets)
[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "
[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "Veri temizleme mini projesinin son adımı, bir matrise dönüştürebileceğimiz ve bir algoritma uygulayabileceğimiz temiz bir metni elde etmektir. İçinde depolanan metindenclean_tweets vektörü kolayca bir kelime matrisine dönüştürebilir ve denetimsiz bir öğrenme algoritması uygulayabiliriz.
Raporlama, büyük veri analitiğinde çok önemlidir. Her kuruluş, karar verme sürecini desteklemek için düzenli bir bilgi kaynağına sahip olmalıdır. Bu görev normalde SQL ve ETL (ayıklama, aktarma ve yükleme) deneyimine sahip veri analistleri tarafından gerçekleştirilir.
Bu görevden sorumlu ekip, büyük veri analitiği bölümünde üretilen bilgileri organizasyonun farklı alanlarına yayma sorumluluğuna sahiptir.
Aşağıdaki örnek, verilerin özetlenmesinin ne anlama geldiğini göstermektedir. Klasöre gidinbda/part1/summarize_data ve klasörün içinde summarize_data.Rprojdosyasını çift tıklayarak. Ardından,summarize_data.R komut dosyasını bulun ve koda bir göz atın ve sunulan açıklamaları izleyin.
# Install the following packages by running the following code in R.
pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')
install.packages(pkgs)ggplot2paketi, veri görselleştirme için mükemmeldir. data.table paket, hızlı ve bellek açısından verimli özetleme yapmak için harika bir seçenektir. R. Son zamanlarda yapılan bir kıyaslama, bunun daha da hızlı olduğunu gösteriyorpandas, benzer görevler için kullanılan python kitaplığı.
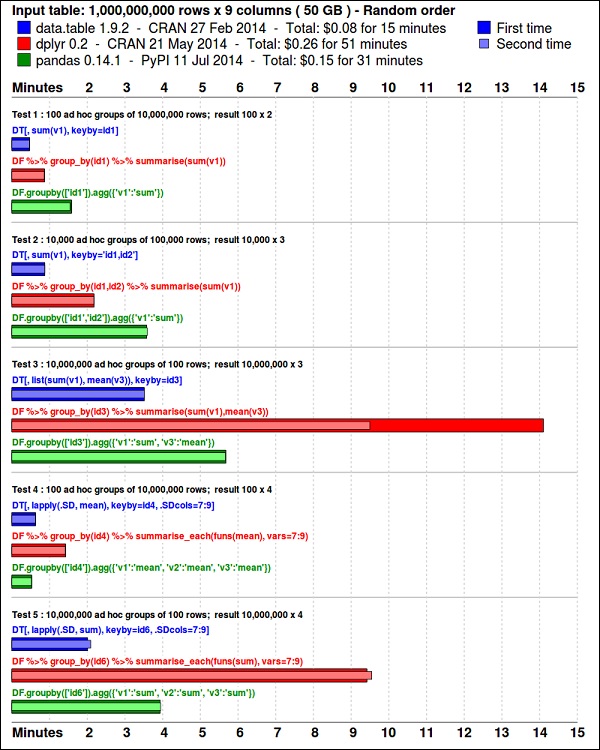
Aşağıdaki kodu kullanarak verilere bir göz atın. Bu kod şu adreste de mevcuttur:bda/part1/summarize_data/summarize_data.Rproj dosya.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Convert the flights data.frame to a data.table object and call it DT
DT <- as.data.table(flights)
# The data has 336776 rows and 16 columns
dim(DT)
# Take a look at the first rows
head(DT)
# year month day dep_time dep_delay arr_time arr_delay carrier
# 1: 2013 1 1 517 2 830 11 UA
# 2: 2013 1 1 533 4 850 20 UA
# 3: 2013 1 1 542 2 923 33 AA
# 4: 2013 1 1 544 -1 1004 -18 B6
# 5: 2013 1 1 554 -6 812 -25 DL
# 6: 2013 1 1 554 -4 740 12 UA
# tailnum flight origin dest air_time distance hour minute
# 1: N14228 1545 EWR IAH 227 1400 5 17
# 2: N24211 1714 LGA IAH 227 1416 5 33
# 3: N619AA 1141 JFK MIA 160 1089 5 42
# 4: N804JB 725 JFK BQN 183 1576 5 44
# 5: N668DN 461 LGA ATL 116 762 5 54
# 6: N39463 1696 EWR ORD 150 719 5 54Aşağıdaki kodda bir veri özetleme örneği vardır.
### Data Summarization
# Compute the mean arrival delay
DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))]
# mean_arrival_delay
# 1: 6.895377
# Now, we compute the same value but for each carrier
mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean1)
# carrier mean_arrival_delay
# 1: UA 3.5580111
# 2: AA 0.3642909
# 3: B6 9.4579733
# 4: DL 1.6443409
# 5: EV 15.7964311
# 6: MQ 10.7747334
# 7: US 2.1295951
# 8: WN 9.6491199
# 9: VX 1.7644644
# 10: FL 20.1159055
# 11: AS -9.9308886
# 12: 9E 7.3796692
# 13: F9 21.9207048
# 14: HA -6.9152047
# 15: YV 15.5569853
# 16: OO 11.9310345
# Now let’s compute to means in the same line of code
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
print(mean2)
# carrier mean_departure_delay mean_arrival_delay
# 1: UA 12.106073 3.5580111
# 2: AA 8.586016 0.3642909
# 3: B6 13.022522 9.4579733
# 4: DL 9.264505 1.6443409
# 5: EV 19.955390 15.7964311
# 6: MQ 10.552041 10.7747334
# 7: US 3.782418 2.1295951
# 8: WN 17.711744 9.6491199
# 9: VX 12.869421 1.7644644
# 10: FL 18.726075 20.1159055
# 11: AS 5.804775 -9.9308886
# 12: 9E 16.725769 7.3796692
# 13: F9 20.215543 21.9207048
# 14: HA 4.900585 -6.9152047
# 15: YV 18.996330 15.5569853
# 16: OO 12.586207 11.9310345
### Create a new variable called gain
# this is the difference between arrival delay and departure delay
DT[, gain:= arr_delay - dep_delay]
# Compute the median gain per carrier
median_gain = DT[, median(gain, na.rm = TRUE), by = carrier]
print(median_gain)Exploratory data analysisJohn Tuckey (1977) tarafından geliştirilen ve yeni bir istatistik perspektifinden oluşan bir kavramdır. Tuckey'nin fikri, geleneksel istatistikte verilerin grafiksel olarak araştırılmaması, sadece hipotezleri test etmek için kullanılmasıydı. Bir araç geliştirmek için ilk girişim Stanford'da yapıldı, projeye prim9 adı verildi . Araç, verileri dokuz boyutta görselleştirebildi, bu nedenle verilerin çok değişkenli bir perspektifini sağlayabildi.
Son günlerde keşifsel veri analizi bir zorunluluktur ve büyük veri analitiği yaşam döngüsüne dahil edilmiştir. Bir organizasyonda içgörü bulma ve bunu etkili bir şekilde iletişim kurma yeteneği, güçlü EDA yetenekleriyle beslenir.
Bell Labs, Tuckey'nin fikirlerine dayanarak, S programming languageistatistik yapmak için etkileşimli bir arayüz sağlamak için. S'nin amacı, kullanımı kolay bir dille kapsamlı grafiksel yetenekler sağlamaktı. Günümüz dünyasında, Büyük Veri bağlamında,R temel alır S programlama dili, analitik için en popüler yazılımdır.
Aşağıdaki program, keşif amaçlı veri analizinin kullanımını göstermektedir.
Aşağıda, keşif amaçlı veri analizine bir örnek verilmiştir. Bu kod şu adreste de mevcuttur:part1/eda/exploratory_data_analysis.R dosya.
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Using the code from the previous section
# This computes the mean arrival and departure delays by carrier.
DT <- as.data.table(flights)
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
# In order to plot data in R usign ggplot, it is normally needed to reshape the data
# We want to have the data in long format for plotting with ggplot
dt = melt(mean2, id.vars = ’carrier’)
# Take a look at the first rows
print(head(dt))
# Take a look at the help for ?geom_point and geom_line to find similar examples
# Here we take the carrier code as the x axis
# the value from the dt data.table goes in the y axis
# The variable column represents the color
p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +
geom_point() + # Plots points
geom_line() + # Plots lines
theme_bw() + # Uses a white background
labs(list(title = 'Mean arrival and departure delay by carrier',
x = 'Carrier', y = 'Mean delay'))
print(p)
# Save the plot to disk
ggsave('mean_delay_by_carrier.png', p,
width = 10.4, height = 5.07)Kod, aşağıdaki gibi bir görüntü oluşturmalıdır -

Verileri anlamak için genellikle görselleştirmek yararlıdır. Normalde Büyük Veri uygulamalarında ilgi, sadece güzel planlar yapmaktan çok içgörü bulmaya dayanır. Aşağıda, grafikleri kullanarak verileri anlamaya yönelik farklı yaklaşımların örnekleri verilmiştir.
Uçuş verilerini analiz etmeye başlamak için sayısal değişkenler arasında korelasyon olup olmadığını kontrol ederek başlayabiliriz. Bu kod şu adreste de mevcuttur:bda/part1/data_visualization/data_visualization.R dosya.
# Install the package corrplot by running
install.packages('corrplot')
# then load the library
library(corrplot)
# Load the following libraries
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# We will continue working with the flights data
DT <- as.data.table(flights)
head(DT) # take a look
# We select the numeric variables after inspecting the first rows.
numeric_variables = c('dep_time', 'dep_delay',
'arr_time', 'arr_delay', 'air_time', 'distance')
# Select numeric variables from the DT data.table
dt_num = DT[, numeric_variables, with = FALSE]
# Compute the correlation matrix of dt_num
cor_mat = cor(dt_num, use = "complete.obs")
print(cor_mat)
### Here is the correlation matrix
# dep_time dep_delay arr_time arr_delay air_time distance
# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373
# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090
# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917
# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776
# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965
# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000
# We can display it visually to get a better understanding of the data
corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")
# save it to disk
png('corrplot.png')
print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))
dev.off()Bu kod, aşağıdaki korelasyon matrisi görselleştirmesini oluşturur -

Grafikte, veri setindeki bazı değişkenler arasında güçlü bir korelasyon olduğunu görebiliriz. Örneğin, varış gecikmesi ve kalkış gecikmesi oldukça ilişkili görünmektedir. Bunu görebiliriz çünkü elips her iki değişken arasında neredeyse çizgisel bir ilişki gösterir, ancak bu sonuçtan nedensellik bulmak kolay değildir.
İki değişken ilişkilendirildiği için birinin diğerine etkisi olduğunu söyleyemeyiz. Ayrıca arsada, hava süresi ile mesafe arasında güçlü bir korelasyon bulduk; bu, daha fazla mesafe ile uçuş süresinin artacağını beklemek oldukça makul.
Verilerin tek değişkenli analizini de yapabiliriz. Dağıtımları görselleştirmenin basit ve etkili bir yolubox-plots. Aşağıdaki kod, ggplot2 kitaplığını kullanarak kutu grafikleri ve kafes grafiklerinin nasıl üretileceğini gösterir. Bu kod şu adreste de mevcuttur:bda/part1/data_visualization/boxplots.R dosya.
source('data_visualization.R')
### Analyzing Distributions using box-plots
# The following shows the distance as a function of the carrier
p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier
in the x axis and distance in the y axis
geom_box-plot() + # Use the box-plot geom
theme_bw() + # Leave a white background - More in line with tufte's
principles than the default
guides(fill = FALSE) + # Remove legend
labs(list(title = 'Distance as a function of carrier', # Add labels
x = 'Carrier', y = 'Distance'))
p
# Save to disk
png(‘boxplot_carrier.png’)
print(p)
dev.off()
# Let's add now another variable, the month of each flight
# We will be using facet_wrap for this
p = ggplot(DT, aes(carrier, distance, fill = carrier)) +
geom_box-plot() +
theme_bw() +
guides(fill = FALSE) +
facet_wrap(~month) + # This creates the trellis plot with the by month variable
labs(list(title = 'Distance as a function of carrier by month',
x = 'Carrier', y = 'Distance'))
p
# The plot shows there aren't clear differences between distance in different months
# Save to disk
png('boxplot_carrier_by_month.png')
print(p)
dev.off()Bu bölüm, kullanıcıları R programlama diliyle tanıştırmaya ayrılmıştır. R, cran web sitesinden indirilebilir . Windows kullanıcıları için rtools ve rstudio IDE'yi kurmak faydalıdır .
Arkasındaki genel konsept R C, C ++ ve Fortran gibi derlenmiş dillerde geliştirilen diğer yazılımlara arayüz olarak hizmet etmek ve kullanıcıya verileri analiz etmek için etkileşimli bir araç sağlamaktır.
Kitap zip dosyasının klasörüne gidin bda/part2/R_introduction ve aç R_introduction.Rprojdosya. Bu bir RStudio oturumu açacaktır. Ardından 01_vectors.R dosyasını açın. Komut dosyasını satır satır çalıştırın ve koddaki açıklamaları izleyin. Öğrenmek için bir başka kullanışlı seçenek de sadece kodu yazmaktır, bu R sözdizimine alışmanıza yardımcı olacaktır. R'de yorumlar # sembolüyle yazılır.
Kitapta çalıştırılan R kodu sonuçlarını görüntülemek için, kod değerlendirildikten sonra, R dönüşleri sonuçları yorumlanır. Bu şekilde, kodu kitaba kopyalayıp yapıştırabilir ve doğrudan R'deki bölümlerini deneyebilirsiniz.
# Create a vector of numbers
numbers = c(1, 2, 3, 4, 5)
print(numbers)
# [1] 1 2 3 4 5
# Create a vector of letters
ltrs = c('a', 'b', 'c', 'd', 'e')
# [1] "a" "b" "c" "d" "e"
# Concatenate both
mixed_vec = c(numbers, ltrs)
print(mixed_vec)
# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"Önceki kodda ne olduğunu inceleyelim. Sayılarla ve harflerle vektörler oluşturmanın mümkün olduğunu görebiliriz. Önceden R'ye ne tür veri istediğimizi söylememize gerek yoktu. Sonunda, hem sayılardan hem de harflerden oluşan bir vektör oluşturmayı başardık. Mixed_vec vektörü sayıları karaktere zorladı, bunu değerlerin tırnak içine nasıl yazdırıldığını görselleştirerek görebiliriz.
Aşağıdaki kod, işlev sınıfı tarafından döndürülen farklı vektörlerin veri türünü gösterir. Bir nesneyi "sorgulamak" ve ona sınıfının ne olduğunu sormak için sınıf işlevini kullanmak yaygındır.
### Evaluate the data types using class
### One dimensional objects
# Integer vector
num = 1:10
class(num)
# [1] "integer"
# Numeric vector, it has a float, 10.5
num = c(1:10, 10.5)
class(num)
# [1] "numeric"
# Character vector
ltrs = letters[1:10]
class(ltrs)
# [1] "character"
# Factor vector
fac = as.factor(ltrs)
class(fac)
# [1] "factor"R, iki boyutlu nesneleri de destekler. Aşağıdaki kodda, R'de kullanılan en popüler iki veri yapısının örnekleri vardır: matrix ve data.frame.
# Matrix
M = matrix(1:12, ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] 1 4 7 10
# [2,] 2 5 8 11
# [3,] 3 6 9 12
lM = matrix(letters[1:12], ncol = 4)
# [,1] [,2] [,3] [,4]
# [1,] "a" "d" "g" "j"
# [2,] "b" "e" "h" "k"
# [3,] "c" "f" "i" "l"
# Coerces the numbers to character
# cbind concatenates two matrices (or vectors) in one matrix
cbind(M, lM)
# [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
# [1,] "1" "4" "7" "10" "a" "d" "g" "j"
# [2,] "2" "5" "8" "11" "b" "e" "h" "k"
# [3,] "3" "6" "9" "12" "c" "f" "i" "l"
class(M)
# [1] "matrix"
class(lM)
# [1] "matrix"
# data.frame
# One of the main objects of R, handles different data types in the same object.
# It is possible to have numeric, character and factor vectors in the same data.frame
df = data.frame(n = 1:5, l = letters[1:5])
df
# n l
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 eÖnceki örnekte gösterildiği gibi, aynı nesnede farklı veri türlerini kullanmak mümkündür. Genel olarak, veri veritabanlarında bu şekilde sunulur, API'ler verilerin bir kısmı metin veya karakter vektörleri ve diğer sayısaldır. Hangi istatistiksel veri türünün atanacağını belirlemek ve ardından bunun için doğru R veri türünü kullanmak analistin işidir. İstatistiklerde normalde değişkenlerin aşağıdaki türlerde olduğunu düşünüyoruz:
- Numeric
- Nominal veya kategorik
- Ordinal
R'de, bir vektör aşağıdaki sınıflardan olabilir -
- Sayısal - Tamsayı
- Factor
- Sıralı Faktör
R, her istatistiksel değişken türü için bir veri türü sağlar. Sıralı faktör nadiren kullanılır, ancak fonksiyon faktörü tarafından oluşturulabilir veya sıralanabilir.
Aşağıdaki bölümde indeksleme kavramı ele alınmaktadır. Bu oldukça yaygın bir işlemdir ve bir nesnenin bölümlerini seçme ve bunlara dönüştürme yapma sorunuyla ilgilenir.
# Let's create a data.frame
df = data.frame(numbers = 1:26, letters)
head(df)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# str gives the structure of a data.frame, it’s a good summary to inspect an object
str(df)
# 'data.frame': 26 obs. of 2 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ... # $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# The latter shows the letters character vector was coerced as a factor.
# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame
# read ?data.frame for more information
class(df)
# [1] "data.frame"
### Indexing
# Get the first row
df[1, ]
# numbers letters
# 1 1 a
# Used for programming normally - returns the output as a list
df[1, , drop = TRUE]
# $numbers # [1] 1 # # $letters
# [1] a
# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z
# Get several rows of the data.frame
df[5:7, ]
# numbers letters
# 5 5 e
# 6 6 f
# 7 7 g
### Add one column that mixes the numeric column with the factor column
df$mixed = paste(df$numbers, df$letters, sep = ’’) str(df) # 'data.frame': 26 obs. of 3 variables: # $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ... # $ mixed : chr "1a" "2b" "3c" "4d" ...
### Get columns
# Get the first column
df[, 1]
# It returns a one dimensional vector with that column
# Get two columns
df2 = df[, 1:2]
head(df2)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# Get the first and third columns
df3 = df[, c(1, 3)]
df3[1:3, ]
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
### Index columns from their names
names(df)
# [1] "numbers" "letters" "mixed"
# This is the best practice in programming, as many times indeces change, but
variable names don’t
# We create a variable with the names we want to subset
keep_vars = c("numbers", "mixed")
df4 = df[, keep_vars]
head(df4)
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
### subset rows and columns
# Keep the first five rows
df5 = df[1:5, keep_vars]
df5
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# subset rows using a logical condition
df6 = df[df$numbers < 10, keep_vars]
df6
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
# 7 7 7g
# 8 8 8h
# 9 9 9iSQL, yapılandırılmış sorgu dilinin kısaltmasıdır. Geleneksel veri ambarlarında ve büyük veri teknolojilerinde veritabanlarından veri çıkarmak için en yaygın kullanılan dillerden biridir. SQL'in temellerini göstermek için örneklerle çalışacağız. Dilin kendisine odaklanmak için R'nin içinde SQL kullanacağız. SQL kodu yazmak açısından bu tam olarak bir veritabanında yapılacağı gibi.
SQL'in çekirdeği üç ifadedir: SELECT, FROM ve WHERE. Aşağıdaki örnekler, SQL'in en yaygın kullanım durumlarını kullanır. Klasöre gidinbda/part2/SQL_introduction ve aç SQL_introduction.Rprojdosya. Sonra 01_select.R komut dosyasını açın. R'de SQL kodu yazmak için,sqldf paketi aşağıdaki kodda gösterildiği gibi.
# Install the sqldf package
install.packages('sqldf')
# load the library
library('sqldf')
library(nycflights13)
# We will be working with the fligths dataset in order to introduce SQL
# Let’s take a look at the table
str(flights)
# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:
# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
# $ month : int 1 1 1 1 1 1 1 1 1 1 ... # $ day : int 1 1 1 1 1 1 1 1 1 1 ...
# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ... # $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ... # $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...
# $ carrier : chr "UA" "UA" "AA" "B6" ... # $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...
# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ... # $ origin : chr "EWR" "LGA" "JFK" "JFK" ...
# $ dest : chr "IAH" "IAH" "MIA" "BQN" ... # $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...
# $ distance : num 1400 1416 1089 1576 762 ... # $ hour : num 5 5 5 5 5 5 5 5 5 5 ...
# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...Select deyimi, tablolardan sütunları almak ve bunlar üzerinde hesaplamalar yapmak için kullanılır. En basit SELECT ifadesi şu şekilde gösterilmiştir:ej1. Ayrıca gösterildiği gibi yeni değişkenler oluşturabiliriz.ej2.
### SELECT statement
ej1 = sqldf("
SELECT
dep_time
,dep_delay
,arr_time
,carrier
,tailnum
FROM
flights
")
head(ej1)
# dep_time dep_delay arr_time carrier tailnum
# 1 517 2 830 UA N14228
# 2 533 4 850 UA N24211
# 3 542 2 923 AA N619AA
# 4 544 -1 1004 B6 N804JB
# 5 554 -6 812 DL N668DN
# 6 554 -4 740 UA N39463
# In R we can use SQL with the sqldf function. It works exactly the same as in
a database
# The data.frame (in this case flights) represents the table we are querying
and goes in the FROM statement
# We can also compute new variables in the select statement using the syntax:
# old_variables as new_variable
ej2 = sqldf("
SELECT
arr_delay - dep_delay as gain,
carrier
FROM
flights
")
ej2[1:5, ]
# gain carrier
# 1 9 UA
# 2 16 UA
# 3 31 AA
# 4 -17 B6
# 5 -19 DLSQL'in en yaygın kullanılan özelliklerinden biri ifadeye göre gruplandırmadır. Bu, başka bir değişkenin farklı grupları için sayısal bir değer hesaplamaya izin verir. 02_group_by.R komut dosyasını açın.
### GROUP BY
# Computing the average
ej3 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
avg(dep_delay) as mean_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# mean_arr_delay mean_dep_delay carrier
# 1 7.3796692 16.725769 9E
# 2 0.3642909 8.586016 AA
# 3 -9.9308886 5.804775 AS
# 4 9.4579733 13.022522 B6
# 5 1.6443409 9.264505 DL
# 6 15.7964311 19.955390 EV
# 7 21.9207048 20.215543 F9
# 8 20.1159055 18.726075 FL
# 9 -6.9152047 4.900585 HA
# 10 10.7747334 10.552041 MQ
# 11 11.9310345 12.586207 OO
# 12 3.5580111 12.106073 UA
# 13 2.1295951 3.782418 US
# 14 1.7644644 12.869421 VX
# 15 9.6491199 17.711744 WN
# 16 15.5569853 18.996330 YV
# Other aggregations
ej4 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
min(dep_delay) as min_dep_delay,
max(dep_delay) as max_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# We can compute the minimun, mean, and maximum values of a numeric value
ej4
# mean_arr_delay min_dep_delay max_dep_delay carrier
# 1 7.3796692 -24 747 9E
# 2 0.3642909 -24 1014 AA
# 3 -9.9308886 -21 225 AS
# 4 9.4579733 -43 502 B6
# 5 1.6443409 -33 960 DL
# 6 15.7964311 -32 548 EV
# 7 21.9207048 -27 853 F9
# 8 20.1159055 -22 602 FL
# 9 -6.9152047 -16 1301 HA
# 10 10.7747334 -26 1137 MQ
# 11 11.9310345 -14 154 OO
# 12 3.5580111 -20 483 UA
# 13 2.1295951 -19 500 US
# 14 1.7644644 -20 653 VX
# 15 9.6491199 -13 471 WN
# 16 15.5569853 -16 387 YV
### We could be also interested in knowing how many observations each carrier has
ej5 = sqldf("
SELECT
carrier, count(*) as count
FROM
flights
GROUP BY
carrier
")
ej5
# carrier count
# 1 9E 18460
# 2 AA 32729
# 3 AS 714
# 4 B6 54635
# 5 DL 48110
# 6 EV 54173
# 7 F9 685
# 8 FL 3260
# 9 HA 342
# 10 MQ 26397
# 11 OO 32
# 12 UA 58665
# 13 US 20536
# 14 VX 5162
# 15 WN 12275
# 16 YV 601SQL'in en kullanışlı özelliği birleştirmelerdir. Birleştirme, her iki tablonun değerlerini eşleştirmek için bir sütun kullanarak tablo A ve tablo B'yi tek bir tabloda birleştirmek istediğimiz anlamına gelir. Pratik olarak, başlamak için farklı türlerde birleştirmeler vardır, bunlar en kullanışlı olanlardır: iç birleştirme ve sol dış birleştirme.
# Let’s create two tables: A and B to demonstrate joins.
A = data.frame(c1 = 1:4, c2 = letters[1:4])
B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])
A
# c1 c2
# 1 a
# 2 b
# 3 c
# 4 d
B
# c1 c2
# 2 b
# 4 c
# 5 d
# 6 e
### INNER JOIN
# This means to match the observations of the column we would join the tables by.
inner = sqldf("
SELECT
A.c1, B.c2
FROM
A INNER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
inner
# c1 c2
# 2 b
# 4 c
### LEFT OUTER JOIN
# the left outer join, sometimes just called left join will return the
# first all the values of the column used from the A table
left = sqldf("
SELECT
A.c1, B.c2
FROM
A LEFT OUTER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
left
# c1 c2
# 1 <NA>
# 2 b
# 3 <NA>
# 4 cVerileri analiz etmenin ilk yaklaşımı, verileri görsel olarak analiz etmektir. Bunu yapmanın hedefleri normalde değişkenler arasındaki ilişkileri ve değişkenlerin tek değişkenli tanımlarını bulmaktır. Bu stratejileri şu şekilde bölebiliriz -
- Tek değişkenli analiz
- Çok değişkenli analiz
Tek Değişkenli Grafik Yöntemler
Univariateistatistiksel bir terimdir. Uygulamada, bir değişkeni verilerin geri kalanından bağımsız olarak analiz etmek istediğimiz anlamına gelir. Bunu verimli bir şekilde yapmaya izin veren araziler:
Kutu Grafikleri
Kutu Grafikleri normalde dağılımları karşılaştırmak için kullanılır. Dağıtımlar arasında farklılıklar olup olmadığını görsel olarak incelemenin harika bir yoludur. Farklı kesimler için elmas fiyatları arasında fark olup olmadığını görebiliriz.
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)Pırlanta fiyatının farklı kesim türlerinde dağılımında farklılıklar olduğunu grafikte görebiliriz.

Histogramlar
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()Yukarıdaki kodun çıktısı aşağıdaki gibi olacaktır -
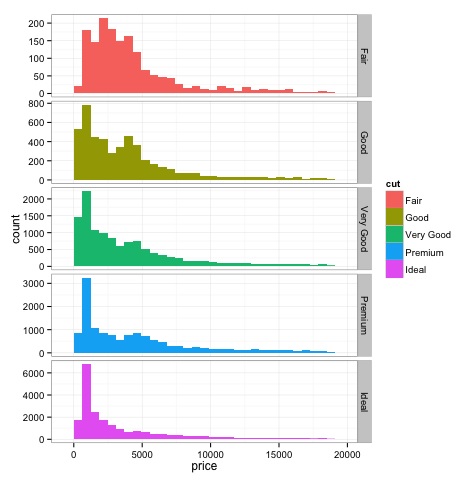
Çok Değişkenli Grafik Yöntemler
Keşifsel veri analizinde çok değişkenli grafik yöntemler, farklı değişkenler arasındaki ilişkileri bulma amacına sahiptir. Bunu başarmanın yaygın olarak kullanılan iki yolu vardır: sayısal değişkenlerden oluşan bir korelasyon matrisini çizmek veya ham verileri basitçe bir dağılım grafikleri matrisi olarak çizmek.
Bunu göstermek için elmas veri setini kullanacağız. Kodu takip etmek için komut dosyasını açınbda/part2/charts/03_multivariate_analysis.R.
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)Kod aşağıdaki çıktıyı üretecektir -

Bu bir özettir, fiyat ve şapka arasında güçlü bir korelasyon olduğunu ve diğer değişkenler arasında pek bir şey olmadığını söyler.
Bir korelasyon matrisi, çok sayıda değişkenimiz olduğunda faydalı olabilir, bu durumda ham verilerin grafiğini çizmek pratik olmaz. Bahsedildiği gibi, ham verileri de göstermek mümkündür -
library(GGally)
ggpairs(df)Grafikte ısı haritasında gösterilen sonuçların doğrulandığını görebiliyoruz, fiyat ve karat değişkenleri arasında 0.922 bir korelasyon var.
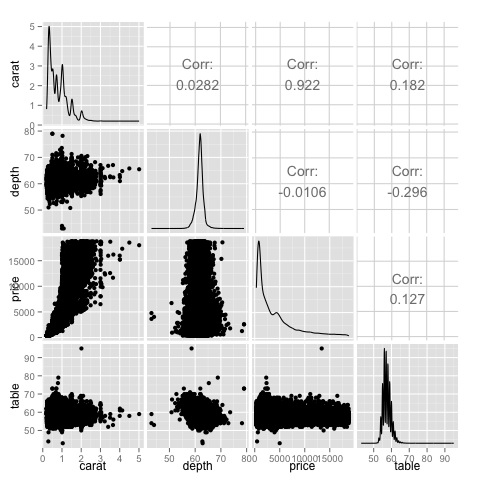
Bu ilişkiyi, dağılım grafiği matrisinin (3, 1) indeksinde yer alan fiyat-karat dağılım grafiğinde görselleştirmek mümkündür.
Bir veri bilimcisinin verileri etkili bir şekilde analiz etmesine olanak tanıyan çeşitli araçlar vardır. Normalde veri analizinin mühendislik yönü veri tabanlarına odaklanır, veri bilimcisi ise veri ürünlerini uygulayabilen araçlara odaklanır. Aşağıdaki bölüm, veri bilimcilerinin pratikte en sık kullandığı istatistiksel paketlere odaklanarak farklı araçların avantajlarını tartışmaktadır.
R Programlama Dili
R, istatistiksel analize odaklanan açık kaynaklı bir programlama dilidir. İstatistiksel yetenekler açısından SAS, SPSS gibi ticari araçlarla rekabet halindedir. C, C ++ veya Fortran gibi diğer programlama dillerine arayüz olduğu düşünülmektedir.
R'nin bir başka avantajı da, mevcut olan çok sayıda açık kaynak kitaplığıdır. CRAN'da ücretsiz olarak indirilebilen 6000'den fazla paket vardır.Github çok çeşitli R paketleri mevcuttur.
Performans açısından, R yoğun işlemler için yavaştır, çünkü çok sayıda kitaplık mevcuttur, kodun yavaş bölümleri derlenmiş dillerde yazılmıştır. Ancak döngüler için derin yazmayı gerektiren işlemler yapmayı planlıyorsanız, o zaman R en iyi alternatifiniz olmayacaktır. Veri analizi amacıyla, gibi güzel kütüphaneler var.data.table, glmnet, ranger, xgboost, ggplot2, caret R'nin daha hızlı programlama dilleri için bir arayüz olarak kullanılmasına izin veren.
Veri analizi için Python
Python genel amaçlı bir programlama dilidir ve veri analizine ayrılmış önemli sayıda kitaplık içerir. pandas, scikit-learn, theano, numpy ve scipy.
R'de mevcut olanların çoğu Python'da da yapılabilir, ancak R'nin kullanımının daha basit olduğunu bulduk. Büyük veri kümeleriyle çalışıyorsanız, normalde Python R'den daha iyi bir seçimdir. Python, verileri satır satır temizlemek ve işlemek için oldukça etkili bir şekilde kullanılabilir. Bu, R'den mümkündür, ancak komut dosyası oluşturma görevleri için Python kadar verimli değildir.
Makine öğrenimi için, scikit-learnorta büyüklükteki veri setlerini sorunsuz bir şekilde işleyebilen çok sayıda algoritmaya sahip güzel bir ortamdır. R'nin eşdeğer kitaplığı (imleç) ile karşılaştırıldığında,scikit-learn daha temiz ve daha tutarlı bir API'ye sahiptir.
Julia
Julia, teknik bilgi işlem için yüksek seviyeli, yüksek performanslı bir dinamik programlama dilidir. Sözdizimi R veya Python'a oldukça benzer, bu nedenle zaten R veya Python ile çalışıyorsanız, Julia'da aynı kodu yazmak oldukça basit olmalıdır. Dil oldukça yeni ve son yıllarda önemli ölçüde büyüdü, bu yüzden şu anda kesinlikle bir seçenek.
Sinir ağları gibi hesaplama açısından yoğun olan prototip oluşturma algoritmaları için Julia'yı öneriyoruz. Araştırma için harika bir araçtır. Üretimde bir model uygulama açısından Python muhtemelen daha iyi alternatiflere sahiptir. Bununla birlikte, R, Python ve Julia'da model uygulama mühendisliğini yapan web hizmetleri olduğu için bu daha az sorun haline geliyor.
SAS
SAS, ticari zeka için halen kullanılmakta olan ticari bir dildir. Kullanıcının çok çeşitli uygulamaları programlamasına izin veren bir temel dile sahiptir. Uzman olmayan kullanıcılara programlama gerektirmeden sinir ağı kitaplığı gibi karmaşık araçları kullanma yeteneği veren epeyce ticari ürün içerir.
Ticari araçların bariz dezavantajının ötesinde, SAS, büyük veri kümelerine iyi ölçeklenemez. Orta ölçekli veri kümeleri bile SAS ile sorun yaşayacak ve sunucunun çökmesine neden olacaktır. Yalnızca küçük veri kümeleriyle çalışıyorsanız ve kullanıcılar uzman veri bilimcisi değilse, SAS önerilmelidir. İleri düzey kullanıcılar için R ve Python daha üretken bir ortam sağlar.
SPSS
SPSS, şu anda istatistiksel analiz için IBM'in bir ürünüdür. Çoğunlukla anket verilerini analiz etmek için kullanılır ve programlayamayan kullanıcılar için iyi bir alternatiftir. Muhtemelen kullanımı SAS kadar basittir, ancak bir modeli uygulama açısından, bir modeli puanlamak için bir SQL kodu sağladığı için daha basittir. Bu kod normalde verimli değildir, ancak bu bir başlangıçtır, ancak SAS, her veritabanı için modelleri ayrı ayrı puanlayan ürünü satmaktadır. Küçük veriler ve deneyimsiz bir ekip için SPSS, SAS kadar iyi bir seçenektir.
Bununla birlikte, yazılım oldukça sınırlıdır ve deneyimli kullanıcılar, R veya Python kullanarak çok daha üretken siparişler alacaktır.
Matlab, Oktav
Matlab veya açık kaynak sürümü (Octave) gibi başka araçlar da mevcuttur. Bu araçlar çoğunlukla araştırma için kullanılmaktadır. Yetenekler açısından R veya Python, Matlab veya Octave'de bulunan her şeyi yapabilir. Yalnızca sağladıkları destekle ilgileniyorsanız, ürünün bir lisansını satın almanız mantıklıdır.
Verileri analiz ederken istatistiksel bir yaklaşıma sahip olmak mümkündür. Temel analizi gerçekleştirmek için gereken temel araçlar şunlardır:
- Korelasyon analizi
- Varyans Analizi
- Hipotez testi
Büyük veri kümeleriyle çalışırken, bu yöntemler Korelasyon Analizi haricinde hesaplama açısından yoğun olmadığından bir sorun içermez. Bu durumda numune almak her zaman mümkündür ve sonuçlar sağlam olmalıdır.
Korelasyon analizi
Korelasyon Analizi, sayısal değişkenler arasında doğrusal ilişkiler bulmaya çalışır. Bu, farklı durumlarda kullanılabilir. Yaygın kullanımlardan biri keşifsel veri analizidir, kitabın 16.0.2 bölümünde bu yaklaşımın temel bir örneği vardır. Her şeyden önce, bahsedilen örnekte kullanılan korelasyon metriği,Pearson coefficient. Bununla birlikte, aykırı değerlerden etkilenmeyen başka bir ilginç korelasyon ölçütü vardır. Bu ölçü, mızrakçı korelasyonu olarak adlandırılır.
spearman correlation metrik, Pearson yöntemine göre aykırı değerlerin varlığına karşı daha sağlamdır ve veriler normal dağılmadığında sayısal değişkenler arasındaki doğrusal ilişkilerin daha iyi tahminlerini verir.
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))Aşağıdaki şekildeki histogramlardan, her iki metriğin korelasyonlarında farklılıklar bekleyebiliriz. Bu durumda, değişkenler açıkça normal dağılmadığından, mızrakçı korelasyonu, sayısal değişkenler arasındaki doğrusal ilişkinin daha iyi bir tahminidir.
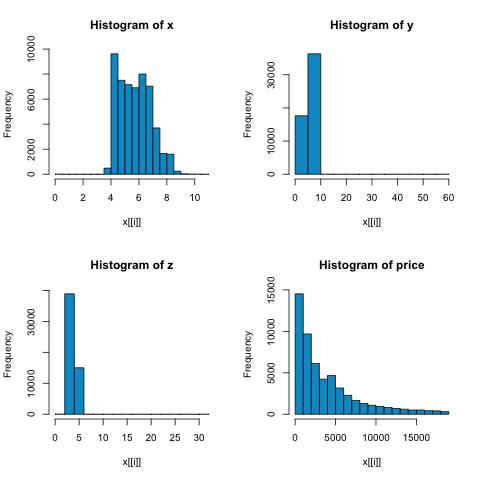
R'deki korelasyonu hesaplamak için dosyayı açın bda/part2/statistical_methods/correlation/correlation.R bu kod bölümüne sahip.
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000Ki-kare Testi
Ki-kare testi, iki rastgele değişkenin bağımsız olup olmadığını test etmemize izin verir. Bu, her bir değişkenin olasılık dağılımının diğerini etkilemediği anlamına gelir. Testi R'de değerlendirmek için önce bir olasılık tablosu oluşturmamız ve ardından tabloyuchisq.test R işlevi.
Örneğin, değişkenler arasında bir ilişki olup olmadığını kontrol edelim: elmas veri kümesinden kesim ve renk. Test resmi olarak şu şekilde tanımlanır:
- H0: Değişken kesim ve elmas bağımsızdır
- H1: Değişken kesim ve elmas bağımsız değil
Bu iki değişken arasında isimleriyle bir ilişki olduğunu varsayabiliriz, ancak test, bu sonucun ne kadar önemli olduğunu söyleyen nesnel bir "kural" verebilir.
Aşağıdaki kod parçacığında, testin p değerinin 2.2e-16 olduğunu bulduk, pratik olarak bu neredeyse sıfırdır. Ardından testi çalıştırdıktan sonraMonte Carlo simulation, p-değerinin 0.0004998 olduğunu bulduk ki bu da 0.05 eşiğinden oldukça düşüktür. Bu sonuç, sıfır hipotezini (H0) reddettiğimiz anlamına gelir, dolayısıyla değişkenlerincut ve color bağımsız değildir.
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998T testi
In fikri t-testnominal değişkenin farklı grupları arasındaki sayısal değişken dağılımında farklılıklar olup olmadığını değerlendirmektir. Bunu göstermek için kesim değişkeninin Orta ve İdeal seviyelerini seçeceğim, ardından bu iki grup arasında sayısal bir değişken olan değerleri karşılaştıracağız.
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542T testleri, R'de t.testişlevi. T.test için formül arabirimi, onu kullanmanın en basit yoludur, fikir, sayısal bir değişkenin bir grup değişkeni tarafından açıklanmasıdır.
Örneğin: t.test(numeric_variable ~ group_variable, data = data). Önceki örnekte,numeric_variable dır-dir price ve group_variable dır-dir cut.
İstatistiksel bir bakış açısıyla, sayısal değişkenin iki grup arasındaki dağılımlarında farklılıklar olup olmadığını test ediyoruz. Resmi olarak hipotez testi, sıfır (H0) hipotezi ve alternatif bir hipotez (H1) ile tanımlanır.
H0: Fiyat değişkeninin Adil ve İdeal grupları arasında dağılımlarında herhangi bir farklılık yoktur.
H1 Fiyat değişkeninin Adil ve İdeal grupları arasında dağılımlarında farklılıklar var
Aşağıdakiler, aşağıdaki kodla R'de uygulanabilir -
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')P değerinin 0.05'ten düşük olup olmadığını kontrol ederek test sonucunu analiz edebiliriz. Durum buysa, alternatif hipotezi koruyoruz. Bu, indirim faktörünün iki seviyesi arasında fiyat farklılıkları bulduğumuz anlamına gelir. Seviye isimlerinden bu sonucu beklerdik, ancak Başarısız grubundaki ortalama fiyatın İdeal gruptakinden daha yüksek olmasını beklemiyorduk. Bunu her faktörün ortalamasını karşılaştırarak görebiliriz.
plotkomutu, fiyat ve kesim değişkeni arasındaki ilişkiyi gösteren bir grafik üretir. Bu bir kutu arsa; Bu grafiği 16.0.1 bölümünde ele aldık, ancak temelde analiz ettiğimiz iki kesim seviyesi için fiyat değişkeninin dağılımını gösteriyor.
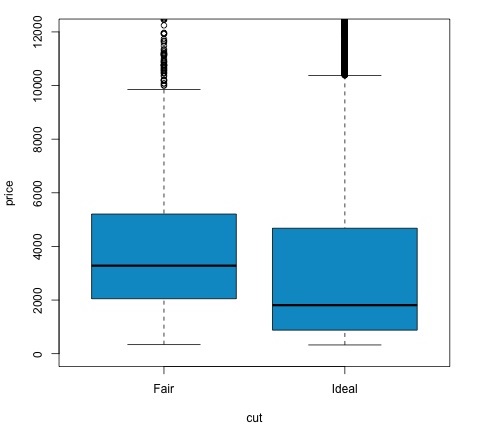
Varyans Analizi
Varyans Analizi (ANOVA), her grubun ortalamasını ve varyansını karşılaştırarak grup dağılımı arasındaki farklılıkları analiz etmek için kullanılan istatistiksel bir modeldir, model Ronald Fisher tarafından geliştirilmiştir. ANOVA, birkaç grubun ortalamalarının eşit olup olmadığına dair istatistiksel bir test sağlar ve bu nedenle t-testini ikiden fazla gruba genelleştirir.
ANOVA'lar, istatistiksel anlamlılık açısından üç veya daha fazla grubu karşılaştırmak için kullanışlıdır, çünkü birden fazla iki örneklemli t testi yapmak, istatistiksel bir tip I hatası yapma şansının artmasına neden olur.
Matematiksel bir açıklama sağlama açısından, testi anlamak için aşağıdakilere ihtiyaç vardır.
x ij = x + (x ben - x) + (x ij - x)
Bu, aşağıdaki modele götürür -
x ij = μ + α ben + ∈ ij
μ genel ortalama ve α i i . grup ortalamasıdır. Hata terimi ∈ ij varsayılır normal dağılımdan istatistiksel bağımsız olması. Testin boş hipotezi şudur:
α 1 = α 2 =… = α k
Test istatistiğinin hesaplanması açısından, iki değeri hesaplamamız gerekiyor -
- Grup farkı için karelerin toplamı -
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- Gruplar içindeki karelerin toplamı
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^2$$
SSD B'nin serbestlik derecesi k − 1 ve SSD W'nin serbestlik derecesi N − k olduğu yerlerde. Daha sonra her bir metrik için ortalama kare farklarını tanımlayabiliriz.
MS B = SSD B / (k - 1)
MS ağırlık = SSD ağırlık / '- (N- k)
Son olarak, ANOVA'daki test istatistiği, yukarıdaki iki miktarın oranı olarak tanımlanır.
F = MS B / MS w
k − 1 ve N − k serbestlik dereceli bir F dağılımını takip eder. Boş hipotez doğruysa, F büyük olasılıkla 1'e yakın olacaktır. Aksi takdirde, gruplar arası ortalama kare MSB muhtemelen büyük olacaktır ve bu da büyük bir F değeriyle sonuçlanır.
Temel olarak ANOVA, toplam varyansın iki kaynağını inceler ve hangi kısmın daha fazla katkıda bulunduğunu görür. Bu nedenle, amaç grup ortalamalarını karşılaştırmak olsa da buna varyans analizi denir.
İstatistiği hesaplamak açısından, aslında R'de yapmak oldukça basittir. Aşağıdaki örnek, bunun nasıl yapıldığını gösterecek ve sonuçların grafiğini çizecektir.
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')Kod aşağıdaki çıktıyı üretecektir -

Örnekte aldığımız p değeri 0.05'ten önemli ölçüde küçüktür, bu nedenle R bunu belirtmek için '***' sembolünü döndürür. Bu, sıfır hipotezini reddettiğimiz ve mpg ortalamaları arasında farklı gruplar arasında farklılıklar bulduğumuz anlamına gelir.cyl değişken.
Makine öğrenimi, örüntü tanıma, bilgisayar görüşü, konuşma tanıma, metin analitiği gibi görevlerle ilgilenen ve istatistik ve matematiksel optimizasyonla güçlü bir bağlantısı olan bilgisayar biliminin bir alt alanıdır. Uygulamalar arasında arama motorlarının geliştirilmesi, spam filtreleme, Optik Karakter Tanıma (OCR) ve diğerleri bulunmaktadır. Veri madenciliği, örüntü tanıma ve istatistiksel öğrenme alanı arasındaki sınırlar net değildir ve temelde tümü benzer sorunlara işaret eder.
Makine öğrenimi iki tür göreve ayrılabilir -
- Denetimli Öğrenme
- Denetimsiz Öğrenme
Denetimli Öğrenme
Denetimli öğrenme, bir X matrisi olarak tanımlanan bir girdi verisinin olduğu ve bir y yanıtını tahmin etmekle ilgilendiğimiz bir tür problemi ifade eder . Burada X = {x 1 x 2 , ..., x, n, } sahiptir , n prediktörleri ve iki değer vardır {C y = 1 c 2 } .
Örnek bir uygulama, bir web kullanıcısının demografik özellikleri tahmin edici olarak kullanarak reklamları tıklama olasılığını tahmin etmektir. Bu genellikle tıklama oranını (TO) tahmin etmek için çağrılır. Sonra y = {tıklama, tıklamaz - tıklama} ve tahmin ediciler, kullanılabilecek diğer özelliklerin yanı sıra kullanılan IP adresi, siteye girdiği gün, kullanıcının şehri, ülkesi olabilir.
Denetimsiz Öğrenme
Denetimsiz öğrenme, öğrenecek bir sınıfa sahip olmadan birbiriyle benzer olan grupları bulma sorunuyla ilgilenir. Tahmin edicilerden, her grupta benzer örnekleri paylaşan ve birbirlerinden farklı olan grupları bulmaya kadar bir eşleme öğrenme görevine yönelik çeşitli yaklaşımlar vardır.
Denetimsiz öğrenmenin örnek bir uygulaması müşteri segmentasyonudur. Örneğin, telekomünikasyon endüstrisinde ortak bir görev, kullanıcıları telefona verdikleri kullanıma göre bölümlere ayırmaktır. Bu, pazarlama departmanının her grubu farklı bir ürünle hedeflemesine izin verecektir.
Naive Bayes, sınıflandırıcılar oluşturmak için olasılıklı bir tekniktir. Saf Bayes sınıflandırıcısının karakteristik varsayımı, belirli bir özelliğin değerinin, sınıf değişkeni göz önüne alındığında, diğer herhangi bir özelliğin değerinden bağımsız olduğunu düşünmektir.
Daha önce bahsedilen aşırı basitleştirilmiş varsayımlara rağmen, saf Bayes sınıflandırıcılarının karmaşık gerçek dünya durumlarında iyi sonuçları vardır. Saf Bayes'in bir avantajı, sınıflandırma için gerekli parametreleri tahmin etmek için yalnızca az miktarda eğitim verisi gerektirmesi ve sınıflandırıcının aşamalı olarak eğitilebilmesidir.
Naive Bayes, bir koşullu olasılık modelidir: sınıflandırılacak bir problem örneği verildiğinde, bir vektörle temsil edilir x= (x 1 ,…, x n ) bazı n özelliği temsil eder (bağımsız değişkenler), bu örneğe K olası sonuç veya sınıfların her biri için olasılıkları atar.
$$p(C_k|x_1,....., x_n)$$
Yukarıdaki formülasyonla ilgili sorun, özelliklerin sayısı n büyükse veya bir özellik çok sayıda değer alabiliyorsa, böyle bir modeli olasılık tablolarına dayandırmanın imkansız olmasıdır. Bu nedenle modeli daha basit hale getirmek için yeniden formüle ediyoruz. Bayes teoremini kullanarak koşullu olasılık şu şekilde ayrıştırılabilir:
$$p(C_k|x) = \frac{p(C_k)p(x|C_k)}{p(x)}$$
Bu, yukarıdaki bağımsızlık varsayımları altında, sınıf değişkeni C üzerindeki koşullu dağılımın -
$$p(C_k|x_1,....., x_n)\: = \: \frac{1}{Z}p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
kanıt nerede Z = p (x) yalnızca x 1 ,…, x n'ye bağlı bir ölçekleme faktörüdür , bu, özellik değişkenlerinin değerleri biliniyorsa bir sabittir. Yaygın bir kural, en olası olan hipotezi seçmektir; bu maksimum a posteriori veya MAP karar kuralı olarak bilinir. Bir Bayes sınıflandırıcısı olan ilgili sınıflandırıcı, bir sınıf etiketi atayan işlevdir.$\hat{y} = C_k$ aşağıdaki gibi bazı k için -
$$\hat{y} = argmax\: p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
Algoritmanın R'de uygulanması basit bir süreçtir. Aşağıdaki örnek, bir Naive Bayes sınıflandırıcısının nasıl eğitildiğini ve bir spam filtreleme probleminde tahmin için nasıl kullanıldığını gösterir.
Aşağıdaki komut dosyası, bda/part3/naive_bayes/naive_bayes.R dosya.
# Install these packages
pkgs = c("klaR", "caret", "ElemStatLearn")
install.packages(pkgs)
library('ElemStatLearn')
library("klaR")
library("caret")
# Split the data in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.9))
train = spam[inx,]
test = spam[-inx,]
# Define a matrix with features, X_train
# And a vector with class labels, y_train
X_train = train[,-58]
y_train = train$spam X_test = test[,-58] y_test = test$spam
# Train the model
nb_model = train(X_train, y_train, method = 'nb',
trControl = trainControl(method = 'cv', number = 3))
# Compute
preds = predict(nb_model$finalModel, X_test)$class
tbl = table(y_test, yhat = preds)
sum(diag(tbl)) / sum(tbl)
# 0.7217391Sonuçtan da görebileceğimiz gibi, Naive Bayes modelinin doğruluğu% 72'dir. Bu, modelin örneklerin% 72'sini doğru şekilde sınıflandırdığı anlamına gelir.
k-ortalamalı kümeleme, n gözlemi, her bir gözlemin en yakın ortalamaya sahip kümeye ait olduğu ve kümenin bir prototipi olarak hizmet ettiği k kümelere bölmeyi amaçlar. Bu, veri alanının Voronoi hücrelerine bölünmesiyle sonuçlanır.
Her bir gözlemin d boyutlu bir gerçek vektör olduğu bir dizi gözlem (x 1 , x 2 ,…, x n ) verildiğinde, k-ortalamalı kümeleme n gözlemleri k gruplarına bölmeyi amaçlar G = {G 1 , G 2 ,…, G k } , aşağıdaki gibi tanımlanan küme içi kareler toplamını (WCSS) en aza indirmek için -
$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x - \mu_{i}\parallel ^2$$
Sonraki formül, k-ortalamalı kümelemede optimal prototipleri bulmak için en aza indirilen objektif işlevi gösterir. Formülün sezgisi, birbirinden farklı gruplar bulmak istediğimiz ve her grubun her üyesinin, her kümenin diğer üyeleriyle benzer olması gerektiğidir.
Aşağıdaki örnek, k-ortalama kümeleme algoritmasının R'de nasıl çalıştırılacağını gösterir.
library(ggplot2)
# Prepare Data
data = mtcars
# We need to scale the data to have zero mean and unit variance
data <- scale(data)
# Determine number of clusters
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:dim(data)[2]) {
wss[i] <- sum(kmeans(data, centers = i)$withinss)
}
# Plot the clusters
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters",
ylab = "Within groups sum of squares")K için iyi bir değer bulmak amacıyla, K'nin farklı değerleri için gruplar içi kareler toplamını çizebiliriz. Bu metrik normalde daha fazla grup eklendikçe azalır, gruplar içindeki azalmanın toplamı olduğu bir nokta bulmak istiyoruz. kareler yavaş yavaş azalmaya başlar. Grafikte, bu değer en iyi K = 6 ile temsil edilir.

Artık K'nin değeri tanımlandığına göre, algoritmayı o değerle çalıştırmak gerekiyor.
# K-Means Cluster Analysis
fit <- kmeans(data, 5) # 5 cluster solution
# get cluster means
aggregate(data,by = list(fit$cluster),FUN = mean)
# append cluster assignment
data <- data.frame(data, fit$cluster)Let Ben = 1 i 2 , ..., i , n ürün adı verilen bir kümesi n ikili özelliklerini olun. Let D = t 1 , t 2 , ..., t m veritabanı olarak adlandırılan bir set işlem olabilir. D'deki her işlemin benzersiz bir işlem kimliği vardır ve I'deki öğelerin bir alt kümesini içerir. Kural, X, Y ⊆ I ve X ∩ Y = ∅ olan X ⇒ Y formunun bir sonucu olarak tanımlanır.
Öğe setlerine (kısa öğe setleri için) X ve Y, kuralın öncülü (sol taraf veya LHS) ve sonucu (sağ taraf veya RHS) olarak adlandırılır.
Kavramları açıklamak için süpermarket alanından küçük bir örnek kullanıyoruz. Öğe seti I = {süt, ekmek, tereyağı, bira} ve öğeleri içeren küçük bir veritabanı aşağıdaki tabloda gösterilmektedir.
| İşlem Kimliği | Öğeler |
|---|---|
| 1 | süt ekmeği |
| 2 | ekmek, tereyağı |
| 3 | bira |
| 4 | süt, ekmek, tereyağı |
| 5 | ekmek, tereyağı |
Süpermarket için örnek bir kural {süt, ekmek} ⇒ {tereyağı} olabilir, yani süt ve ekmek alınırsa müşteriler de tereyağı satın alır. Olası tüm kurallar kümesinden ilginç kurallar seçmek için, çeşitli önem ve ilgi ölçütleri üzerindeki kısıtlamalar kullanılabilir. En iyi bilinen kısıtlamalar, destek ve güven konusunda minimum eşik değerlerdir.
Bir öğe-setinin (X) destek desteği (X), öğe setini içeren veri setindeki işlemlerin oranı olarak tanımlanır. Tablo 1'deki örnek veri tabanında, ürün seti {süt, ekmek}, tüm işlemlerin% 40'ında (5 işlemden 2'si) olduğu için 2/5 = 0,4'lük bir desteğe sahiptir. Sık ürün setlerini bulmak, denetimsiz öğrenme probleminin basitleştirilmesi olarak görülebilir.
Bir kuralın güvenirliği, conf (X ⇒ Y) = supp (X ∪ Y) / supp (X) olarak tanımlanır. Örneğin, Tablo 1'deki veritabanında {süt, ekmek} ⇒ {tereyağı} kuralı 0,2 / 0,4 = 0,5'lik bir güvene sahiptir, bu da süt ve ekmek içeren işlemlerin% 50'si için kuralın doğru olduğu anlamına gelir. Güven, bu işlemlerin LHS'yi de içermesi koşuluyla, işlemlerde kuralın sağlığını bulma olasılığı olan P (Y | X) olasılığının bir tahmini olarak yorumlanabilir.
Bulunan komut dosyasında bda/part3/apriori.R uygulama kodu apriori algorithm bulunabilir.
# Load the library for doing association rules
# install.packages(’arules’)
library(arules)
# Data preprocessing
data("AdultUCI")
AdultUCI[1:2,]
AdultUCI[["fnlwgt"]] <- NULL
AdultUCI[["education-num"]] <- NULL
AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),
labels = c("Young", "Middle-aged", "Senior", "Old"))
AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]],
c(0,25,40,60,168)), labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],
c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capitalgain"]]>0]),Inf)),
labels = c("None", "Low", "High"))
AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],
c(-Inf,0, median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capitalloss"]]>0]),Inf)),
labels = c("none", "low", "high"))Apriori algoritmasını kullanarak kurallar oluşturmak için bir işlem matrisi oluşturmamız gerekir. Aşağıdaki kod, bunun R'de nasıl yapılacağını gösterir.
# Convert the data into a transactions format
Adult <- as(AdultUCI, "transactions")
Adult
# transactions in sparse format with
# 48842 transactions (rows) and
# 115 items (columns)
summary(Adult)
# Plot frequent item-sets
itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)
# generate rules
min_support = 0.01
confidence = 0.6
rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))
rules
inspect(rules[100:110, ])
# lhs rhs support confidence lift
# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486
# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456
# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474
= United-States}Karar Ağacı, sınıflandırma veya regresyon gibi denetimli öğrenme problemleri için kullanılan bir algoritmadır. Karar ağacı veya sınıflandırma ağacı, her dahili (yaprak olmayan) düğümün bir giriş özelliği ile etiketlendiği bir ağaçtır. Bir özellik ile etiketlenmiş bir düğümden gelen yaylar, özelliğin olası değerlerinin her biri ile etiketlenir. Ağacın her yaprağı bir sınıfla veya sınıflar üzerindeki olasılık dağılımıyla etiketlenir.
Bir ağaç, kaynak kümesini bir öznitelik değeri testine göre alt kümelere bölerek "öğrenilebilir". Bu işlem, türetilmiş her alt kümede adı verilen özyineli bir şekilde tekrarlanırrecursive partitioning. Yineleme, bir düğümdeki alt küme hedef değişkenin tüm değerine sahip olduğunda veya bölme artık tahminlere değer katmadığında tamamlanır. Karar ağaçlarının bu yukarıdan aşağıya indüksiyon süreci, açgözlü bir algoritmanın bir örneğidir ve karar ağaçlarını öğrenmek için en yaygın stratejidir.
Veri madenciliğinde kullanılan karar ağaçları iki ana türdendir -
Classification tree - yanıt nominal bir değişken olduğunda, örneğin bir e-postanın istenmeyen posta olup olmadığı.
Regression tree - tahmin edilen sonucun gerçek bir sayı olarak kabul edilebildiği durumlarda (örneğin bir işçinin maaşı).
Karar ağaçları basit bir yöntemdir ve bu nedenle bazı sorunları vardır. Bu sorunlardan biri, karar ağaçlarının ürettiği sonuç modellerinde yüksek varyans olmasıdır. Bu sorunu hafifletmek için karar ağaçlarının toplu yöntemleri geliştirilmiştir. Şu anda yaygın olarak kullanılan iki grup yöntem grubu vardır -
Bagging decision trees- Bu ağaçlar, eğitim verilerini değiştirerek tekrar tekrar örnekleyerek ve ağaçları bir fikir birliği tahmini için oylayarak çoklu karar ağaçları oluşturmak için kullanılır. Bu algoritmaya rastgele orman adı verilmiştir.
Boosting decision trees- Gradyan artırma, zayıf öğrencileri birleştirir; bu durumda, karar ağaçları yinelemeli bir şekilde tek bir güçlü öğrenciye dönüşür. Zayıf bir ağacı veriye sığdırır ve önceki modelin hatasını düzeltmek için zayıf öğrencileri tekrar tekrar uydurmaya devam eder.
# Install the party package
# install.packages('party')
library(party)
library(ggplot2)
head(diamonds)
# We will predict the cut of diamonds using the features available in the
diamonds dataset.
ct = ctree(cut ~ ., data = diamonds)
# plot(ct, main="Conditional Inference Tree")
# Example output
# Response: cut
# Inputs: carat, color, clarity, depth, table, price, x, y, z
# Number of observations: 53940
#
# 1) table <= 57; criterion = 1, statistic = 10131.878
# 2) depth <= 63; criterion = 1, statistic = 8377.279
# 3) table <= 56.4; criterion = 1, statistic = 226.423
# 4) z <= 2.64; criterion = 1, statistic = 70.393
# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48
# 6) color <= E; criterion = 0.997, statistic = 12.829
# 7)* weights = 82
# 6) color > E
#Table of prediction errors
table(predict(ct), diamonds$cut)
# Fair Good Very Good Premium Ideal
# Fair 1388 171 17 0 14
# Good 102 2912 499 26 27
# Very Good 54 998 3334 249 355
# Premium 44 711 5054 11915 1167
# Ideal 22 114 3178 1601 19988
# Estimated class probabilities
probs = predict(ct, newdata = diamonds, type = "prob")
probs = do.call(rbind, probs)
head(probs)Lojistik regresyon, yanıt değişkeninin kategorik olduğu bir sınıflandırma modelidir. İstatistiklerden gelen ve denetimli sınıflandırma problemleri için kullanılan bir algoritmadır. Lojistik regresyonda, aşağıdaki denklemde maliyet fonksiyonunu en aza indiren parametrelerin vektörünü β bulmaya çalışıyoruz.
$$logit(p_i) = ln \left ( \frac{p_i}{1 - p_i} \right ) = \beta_0 + \beta_1x_{1,i} + ... + \beta_kx_{k,i}$$
Aşağıdaki kod, R'ye lojistik regresyon modelinin nasıl yerleştirileceğini gösterir. Burada, Naive Bayes için kullanılanın aynısı olan lojistik regresyonu göstermek için spam veri setini kullanacağız.
Doğruluk açısından tahmin sonuçlarından, regresyon modelinin, Naive Bayes sınıflandırıcısı tarafından elde edilen% 72'ye kıyasla, test setinde% 92,5'lik bir doğruluk elde ettiğini bulduk.
library(ElemStatLearn)
head(spam)
# Split dataset in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.8))
train = spam[inx,]
test = spam[-inx,]
# Fit regression model
fit = glm(spam ~ ., data = train, family = binomial())
summary(fit)
# Call:
# glm(formula = spam ~ ., family = binomial(), data = train)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -4.5172 -0.2039 0.0000 0.1111 5.4944
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 ***
# A.1 -4.546e-01 2.560e-01 -1.776 0.075720 .
# A.2 -1.630e-01 7.731e-02 -2.108 0.035043 *
# A.3 1.487e-01 1.261e-01 1.179 0.238591
# A.4 2.055e+00 1.467e+00 1.401 0.161153
# A.5 6.165e-01 1.191e-01 5.177 2.25e-07 ***
# A.6 7.156e-01 2.768e-01 2.585 0.009747 **
# A.7 2.606e+00 3.917e-01 6.652 2.88e-11 ***
# A.8 6.750e-01 2.284e-01 2.955 0.003127 **
# A.9 1.197e+00 3.362e-01 3.559 0.000373 ***
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
### Make predictions
preds = predict(fit, test, type = ’response’)
preds = ifelse(preds > 0.5, 1, 0)
tbl = table(target = test$spam, preds)
tbl
# preds
# target 0 1
# email 535 23
# spam 46 316
sum(diag(tbl)) / sum(tbl)
# 0.925Zaman serisi, bir tarihe veya zaman damgasına göre indekslenmiş kategorik veya sayısal değişkenlerin bir gözlem dizisidir. Zaman serisi verilerinin net bir örneği, hisse senedi fiyatının zaman serisidir. Aşağıdaki tabloda zaman serisi verilerinin temel yapısını görebiliriz. Bu durumda gözlemler her saat kaydedilir.
| Zaman damgası | Hisse senedi fiyatı |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
Normalde, zaman serisi analizinin ilk adımı seriyi çizmektir, bu normalde bir çizgi grafikle yapılır.
Zaman serisi analizinin en yaygın uygulaması, verilerin zamansal yapısını kullanarak sayısal bir değerin gelecekteki değerlerini tahmin etmektir. Bu, mevcut gözlemlerin gelecekteki değerleri tahmin etmek için kullanıldığı anlamına gelir.
Verilerin zamansal sıralaması, geleneksel regresyon yöntemlerinin kullanışlı olmadığı anlamına gelir. Sağlam bir tahmin oluşturmak için, verilerin zamansal sıralanmasını hesaba katan modellere ihtiyacımız var.
Zaman Serisi Analizi için en yaygın kullanılan modele Autoregressive Moving Average(ARMA). Model iki bölümden oluşmaktadır:autoregressive (AR) bölümü ve bir moving average(MA) bölümü. Model genellikle daha sonra ARMA (p, q) modeli olarak adlandırılır , burada p , otoregresif bölümün sırası ve q , hareketli ortalama bölümün sırasıdır.
Otoregresif Model
AR (p) sipariş p bir kendiliğinden gerileyen modeli olarak okunur. Matematiksel olarak şöyle yazılır -
$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$
burada {φ 1 ,…, φ p } tahmin edilecek parametrelerdir, c sabittir ve rastgele değişken ε t beyaz gürültüyü temsil eder. Modelin sabit kalması için parametrelerin değerleri üzerinde bazı kısıtlamalar gereklidir.
Hareketli ortalama
Gösterimde MA (q) sipariş hareketli ortalama modeline değinmektedir q -
$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$
θ 1 , ..., θ q modelin parametreleridir, μ X t'nin beklentisidir ve ε t , ε t - 1 , ... beyaz gürültü hatası terimleridir.
Otoregresif Hareketli Ortalama
ARMA (p, q) modeli birleştirir s kendiliğinden gerileyen koşulları ve q hareketli ortalama şartları. Model matematiksel olarak aşağıdaki formülle ifade edilir -
$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$
Biz görebilirsiniz ARMA (p, q) modeli bir kombinasyonudur AR (p) ve MA (q) model.
Modelin bazı sezgi vermek denklemin AR parçası X için parametreleri tahmin etmeyi amaçlayan düşünün i - t X değişkenin değerini tahmin etmek amacıyla gözlemlerini t . Sonunda, geçmiş değerlerin ağırlıklı ortalamasıdır. MA bölümü aynı yaklaşımı kullanır, ancak önceki gözlemlerin hatasıyla, ε t - i . Sonuç olarak, modelin sonucu ağırlıklı ortalamadır.
Aşağıdaki kod parçacığı , R'de bir ARMA'nın (p, q) nasıl uygulanacağını gösterir .
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)Verilerin grafiğini çizmek, normalde verilerde zamansal bir yapı olup olmadığını bulmak için ilk adımdır. Her yılın sonunda güçlü ani artışlar olduğunu arsadan görebiliyoruz.
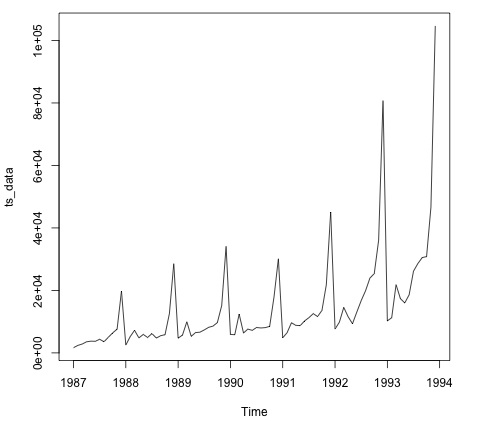
Aşağıdaki kod, bir ARMA modelini verilere uyar. Birkaç model kombinasyonunu çalıştırır ve daha az hatası olanı seçer.
# Fit the ARMA model
fit = auto.arima(ts_data)
summary(fit)
# Series: ts_data
# ARIMA(1,1,1)(0,1,1)[12]
# Coefficients:
# ar1 ma1 sma1
# 0.2401 -0.9013 0.7499
# s.e. 0.1427 0.0709 0.1790
#
# sigma^2 estimated as 15464184: log likelihood = -693.69
# AIC = 1395.38 AICc = 1395.98 BIC = 1404.43
# Training set error measures:
# ME RMSE MAE MPE MAPE MASE ACF1
# Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172Bu bölümde, kitabın 1. bölümünde kazınan verileri kullanacağız. Veriler, serbest çalışanların profillerini ve USD cinsinden ücretlendirdikleri saatlik ücreti açıklayan bir metne sahiptir. Aşağıdaki bölümün fikri, bir serbest meslek sahibinin becerilerini göz önünde bulunduran bir modele uymaktır, saatlik maaşını tahmin edebiliriz.
Aşağıdaki kod, bu durumda kullanıcının becerilerine sahip olan ham metnin bir kelime matrisi torbasında nasıl dönüştürüleceğini gösterir. Bunun için tm adlı bir R kütüphanesi kullanıyoruz. Bu, derlemedeki her kelime için, her bir değişkenin gerçekleşme miktarıyla değişken oluşturduğumuz anlamına gelir.
library(tm)
library(data.table)
source('text_analytics/text_analytics_functions.R')
data = fread('text_analytics/data/profiles.txt')
rate = as.numeric(data$rate)
keep = !is.na(rate)
rate = rate[keep]
### Make bag of words of title and body
X_all = bag_words(data$user_skills[keep])
X_all = removeSparseTerms(X_all, 0.999)
X_all
# <<DocumentTermMatrix (documents: 389, terms: 1422)>>
# Non-/sparse entries: 4057/549101
# Sparsity : 99%
# Maximal term length: 80
# Weighting : term frequency - inverse document frequency (normalized) (tf-idf)
### Make a sparse matrix with all the data
X_all <- as_sparseMatrix(X_all)Artık seyrek bir matris olarak temsil edilen metne sahip olduğumuza göre, seyrek bir çözüm verecek bir model sığdırabiliriz. Bu durum için iyi bir alternatif, LASSO (en az mutlak büzülme ve seçim operatörü) kullanmaktır. Bu, hedefi tahmin etmek için en uygun özellikleri seçebilen bir regresyon modelidir.
train_inx = 1:200
X_train = X_all[train_inx, ]
y_train = rate[train_inx]
X_test = X_all[-train_inx, ]
y_test = rate[-train_inx]
# Train a regression model
library(glmnet)
fit <- cv.glmnet(x = X_train, y = y_train,
family = 'gaussian', alpha = 1,
nfolds = 3, type.measure = 'mae')
plot(fit)
# Make predictions
predictions = predict(fit, newx = X_test)
predictions = as.vector(predictions[,1])
head(predictions)
# 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367
# We can compute the mean absolute error for the test data
mean(abs(y_test - predictions))
# 15.02175Şimdi, bir serbest meslek sahibinin saatlik maaşını tahmin edebilen bir dizi beceri verilen bir modelimiz var. Daha fazla veri toplanırsa, modelin performansı artacaktır, ancak bu ardışık düzeni uygulayacak kod aynı olacaktır.
Çevrimiçi öğrenme, denetimli öğrenim modellerinin çok büyük veri kümelerine ölçeklenmesine olanak tanıyan bir makine öğrenimi alt alanıdır. Temel fikir, bir modeli sığdırmak için bellekteki tüm verileri okumamıza gerek olmadığıdır, yalnızca her bir örneği bir seferde okumamız gerekir.
Bu durumda, lojistik regresyon kullanarak bir çevrimiçi öğrenme algoritmasının nasıl uygulanacağını göstereceğiz. Denetimli öğrenme algoritmalarının çoğunda olduğu gibi, minimize edilmiş bir maliyet işlevi vardır. Lojistik regresyonda, maliyet fonksiyonu şu şekilde tanımlanır:
$$ J (\ theta) \: = \: \ frac {-1} {m} \ left [\ sum_ {i = 1} ^ {m} y ^ {(i)} log (h _ {\ theta} ( x ^ {(i)})) + (1 - y ^ {(i)}) günlük (1 - h _ {\ theta} (x ^ {(i)})) \ sağ] $$
burada J (θ) maliyet fonksiyonunu ve h θ (x) hipotezi temsil eder. Lojistik regresyon durumunda, aşağıdaki formülle tanımlanır -
$$ h_ \ theta (x) = \ frac {1} {1 + e ^ {\ theta ^ T x}} $$
Artık maliyet fonksiyonunu tanımladığımıza göre, onu en aza indirmek için bir algoritma bulmamız gerekiyor. Bunu başarmak için en basit algoritmaya stokastik gradyan inişi denir. Lojistik regresyon modelinin ağırlıkları için algoritmanın güncelleme kuralı şu şekilde tanımlanır:
$$ \ theta_j: = \ theta_j - \ alpha (h_ \ theta (x) - y) x $$
Aşağıdaki algoritmanın birkaç uygulaması vardır, ancak vowpal wabbit kitaplığında uygulanan algoritma en gelişmiş olanıdır. Kütüphane, büyük ölçekli regresyon modellerinin eğitimine izin verir ve az miktarda RAM kullanır. Yaratıcıların kendi sözleriyle, "Vowpal Wabbit (VW) projesi, Microsoft Research ve (daha önce) Yahoo! Research tarafından desteklenen hızlı bir çekirdek dışı öğrenme sistemidir" olarak tanımlanmaktadır.
Titanik veri setiyle çalışacağız. kagglerekabet. Orijinal veriler şurada bulunabilir:bda/part3/vwKlasör. Burada iki dosyamız var -
- Eğitim verilerimiz var (train_titanic.csv) ve
- yeni tahminler yapmak için etiketlenmemiş veriler (test_titanic.csv).
Csv formatını vowpal wabbit giriş formatı kullanın csv_to_vowpal_wabbit.pypython komut dosyası. Bunun için kesinlikle python yüklemeniz gerekecek. Şuraya gidin:bda/part3/vw klasör, terminali açın ve aşağıdaki komutu yürütün -
python csv_to_vowpal_wabbit.pyBu bölüm için, Windows kullanıyorsanız, bir Unix komut satırı kurmanız gerekeceğini unutmayın, bunun için cygwin web sitesine girin .
Terminali açın ve ayrıca klasörde bda/part3/vw ve aşağıdaki komutu çalıştırın -
vw train_titanic.vw -f model.vw --binary --passes 20 -c -q ff --sgd --l1
0.00000001 --l2 0.0000001 --learning_rate 0.5 --loss_function logisticHer argümanın ne olduğunu parçalayalım vw call anlamına geliyor.
-f model.vw - modeli daha sonra tahminler yapmak için model.vw dosyasına kaydettiğimiz anlamına gelir
--binary -1,1 etiketlerle ikili sınıflandırma olarak kaybı bildirir
--passes 20 - Veriler ağırlıkları öğrenmek için 20 kez kullanılır
-c - bir önbellek dosyası oluşturun
-q ff - f ad alanında ikinci dereceden özellikler kullanın
--sgd - Düzenli / klasik / basit stokastik gradyan iniş güncellemesini kullanın, yani adaptif olmayan, normalize edilmeyen ve değişmeyen olmayan.
--l1 --l2 - L1 ve L2 normunun düzenlenmesi
--learning_rate 0.5 - Güncelleme kuralı formülünde tanımlanan öğrenme oranı α
Aşağıdaki kod, regresyon modelini komut satırında çalıştırmanın sonuçlarını gösterir. Sonuçlarda, ortalama günlük kaybını ve algoritma performansının küçük bir raporunu alıyoruz.
-loss_function logistic
creating quadratic features for pairs: ff
using l1 regularization = 1e-08
using l2 regularization = 1e-07
final_regressor = model.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 1
power_t = 0.5
decay_learning_rate = 1
using cache_file = train_titanic.vw.cache
ignoring text input in favor of cache input
num sources = 1
average since example example current current current
loss last counter weight label predict features
0.000000 0.000000 1 1.0 -1.0000 -1.0000 57
0.500000 1.000000 2 2.0 1.0000 -1.0000 57
0.250000 0.000000 4 4.0 1.0000 1.0000 57
0.375000 0.500000 8 8.0 -1.0000 -1.0000 73
0.625000 0.875000 16 16.0 -1.0000 1.0000 73
0.468750 0.312500 32 32.0 -1.0000 -1.0000 57
0.468750 0.468750 64 64.0 -1.0000 1.0000 43
0.375000 0.281250 128 128.0 1.0000 -1.0000 43
0.351562 0.328125 256 256.0 1.0000 -1.0000 43
0.359375 0.367188 512 512.0 -1.0000 1.0000 57
0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h
0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h
0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h
0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h
finished run
number of examples per pass = 802
passes used = 11
weighted example sum = 8822
weighted label sum = -2288
average loss = 0.179775 h
best constant = -0.530826
best constant’s loss = 0.659128
total feature number = 427878Şimdi kullanabiliriz model.vw yeni verilerle tahminler üretmek için eğitim aldık.
vw -d test_titanic.vw -t -i model.vw -p predictions.txtÖnceki komutta oluşturulan tahminler [0, 1] aralığı arasına sığacak şekilde normalleştirilmemiştir. Bunu yapmak için sigmoid dönüşüm kullanıyoruz.
# Read the predictions
preds = fread('vw/predictions.txt')
# Define the sigmoid function
sigmoid = function(x) {
1 / (1 + exp(-x))
}
probs = sigmoid(preds[[1]])
# Generate class labels
preds = ifelse(probs > 0.5, 1, 0)
head(preds)
# [1] 0 1 0 0 1 0