Büyük Veri Analitiği - İstatistiksel Yöntemler
Verileri analiz ederken istatistiksel bir yaklaşıma sahip olmak mümkündür. Temel analizi gerçekleştirmek için gereken temel araçlar şunlardır:
- Korelasyon analizi
- Varyans Analizi
- Hipotez testi
Büyük veri kümeleriyle çalışırken, bu yöntemler Korelasyon Analizi haricinde hesaplama açısından yoğun olmadığından bir sorun içermez. Bu durumda numune almak her zaman mümkündür ve sonuçlar sağlam olmalıdır.
Korelasyon analizi
Korelasyon Analizi, sayısal değişkenler arasında doğrusal ilişkiler bulmaya çalışır. Bu, farklı durumlarda kullanılabilir. Yaygın kullanımlardan biri keşifsel veri analizidir, kitabın 16.0.2 bölümünde bu yaklaşımın temel bir örneği vardır. Her şeyden önce, bahsedilen örnekte kullanılan korelasyon metriği,Pearson coefficient. Bununla birlikte, aykırı değerlerden etkilenmeyen başka bir ilginç korelasyon ölçütü vardır. Bu ölçü, mızrakçı korelasyonu olarak adlandırılır.
spearman correlation metrik, Pearson yöntemine göre aykırı değerlerin varlığına karşı daha sağlamdır ve veriler normal dağılmadığında sayısal değişkenler arasındaki doğrusal ilişkilerin daha iyi tahminlerini verir.
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))Aşağıdaki şekildeki histogramlardan, her iki ölçümün korelasyonlarında farklılıklar bekleyebiliriz. Bu durumda, değişkenler açıkça normal dağılmadığından, mızrakçı korelasyonu, sayısal değişkenler arasındaki doğrusal ilişkinin daha iyi bir tahminidir.
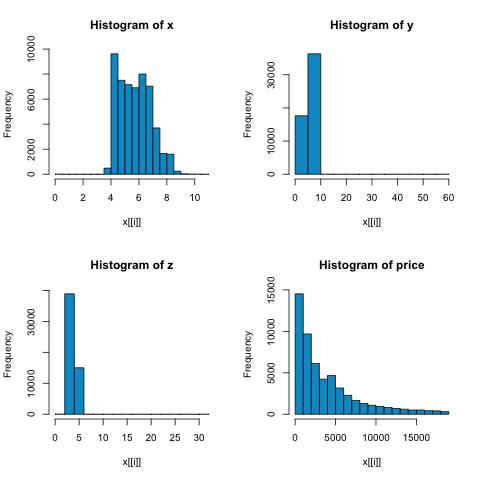
R'deki korelasyonu hesaplamak için dosyayı açın bda/part2/statistical_methods/correlation/correlation.R bu kod bölümüne sahip.
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000Ki-kare Testi
Ki-kare testi, iki rastgele değişkenin bağımsız olup olmadığını test etmemizi sağlar. Bu, her bir değişkenin olasılık dağılımının diğerini etkilemediği anlamına gelir. Testi R'de değerlendirmek için önce bir olasılık tablosu oluşturmamız ve ardından tabloyuchisq.test R işlevi.
Örneğin, değişkenler arasında bir ilişki olup olmadığını kontrol edelim: elmas veri kümesinden kesim ve renk. Test resmi olarak şu şekilde tanımlanır:
- H0: Değişken kesim ve elmas bağımsızdır
- H1: Değişken kesim ve elmas bağımsız değil
Bu iki değişken arasında isimleriyle bir ilişki olduğunu varsayabiliriz, ancak test, bu sonucun ne kadar önemli olduğunu söyleyen nesnel bir "kural" verebilir.
Aşağıdaki kod parçacığında, testin p değerinin 2.2e-16 olduğunu bulduk, pratik olarak bu neredeyse sıfırdır. Ardından testi çalıştırdıktan sonraMonte Carlo simulation, p-değerinin 0.0004998 olduğunu bulduk ki bu da 0.05 eşiğinden oldukça düşüktür. Bu sonuç, sıfır hipotezini (H0) reddettiğimiz anlamına gelir, dolayısıyla değişkenlerincut ve color bağımsız değildir.
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998T testi
In fikri t-testnominal değişkenin farklı grupları arasında sayısal bir değişken dağılımında farklılıklar olup olmadığını değerlendirmektir. Bunu göstermek için kesim değişkeninin Orta ve İdeal seviyelerini seçeceğim, ardından bu iki grup arasında sayısal bir değişken olan değerleri karşılaştıracağız.
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542T testleri, R'de t.testişlevi. T.test için formül arayüzü, onu kullanmanın en basit yoludur, fikir, sayısal bir değişkenin bir grup değişkeni tarafından açıklanmasıdır.
Örneğin: t.test(numeric_variable ~ group_variable, data = data). Önceki örnekte,numeric_variable dır-dir price ve group_variable dır-dir cut.
İstatistiksel bir bakış açısıyla, sayısal değişkenin dağılımlarında iki grup arasında farklılıklar olup olmadığını test ediyoruz. Resmi olarak hipotez testi, sıfır (H0) hipotezi ve alternatif bir hipotez (H1) ile tanımlanır.
H0: Fiyat değişkeninin Adil ve İdeal grupları arasında dağılımlarında herhangi bir farklılık yoktur.
H1 Fiyat değişkeninin Adil ve İdeal grupları arasında dağılımlarında farklılıklar var
Aşağıdakiler, aşağıdaki kodla R'de uygulanabilir -
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
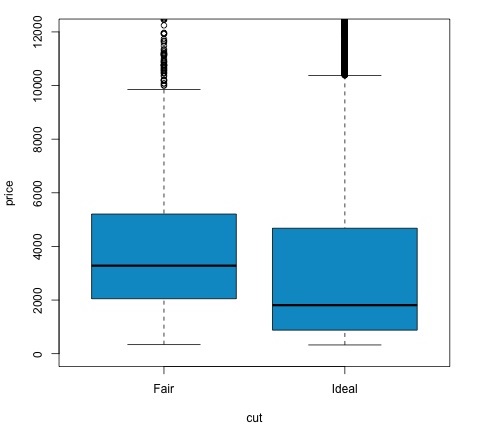
col = 'deepskyblue3')P değerinin 0.05'ten düşük olup olmadığını kontrol ederek test sonucunu analiz edebiliriz. Durum buysa, alternatif hipotezi devam ettiriyoruz. Bu, indirim faktörünün iki seviyesi arasında fiyat farklılıkları bulduğumuz anlamına gelir. Seviyelerin isimlerinden bu sonucu beklerdik, ancak Başarısız grubundaki ortalama fiyatın İdeal gruptan daha yüksek olmasını beklemiyorduk. Bunu, her bir faktörün ortalamasını karşılaştırarak görebiliriz.
plotkomutu, fiyat ve kesim değişkeni arasındaki ilişkiyi gösteren bir grafik üretir. Bu bir kutu arsa; Bu grafiği 16.0.1 bölümünde ele aldık, ancak temelde analiz ettiğimiz iki kesim seviyesi için fiyat değişkeninin dağılımını gösteriyor.
Varyans Analizi
Varyans Analizi (ANOVA), her grubun ortalamasını ve varyansını karşılaştırarak grup dağılımı arasındaki farklılıkları analiz etmek için kullanılan istatistiksel bir modeldir, model Ronald Fisher tarafından geliştirilmiştir. ANOVA, birkaç grubun ortalamasının eşit olup olmadığına dair istatistiksel bir test sağlar ve bu nedenle t testini ikiden fazla gruba genelleştirir.
ANOVA'lar, istatistiksel anlamlılık açısından üç veya daha fazla grubu karşılaştırmak için kullanışlıdır, çünkü birden fazla iki örneklemli t-testi yapmak, istatistiksel bir tip I hatası yapma şansının artmasına neden olur.
Matematiksel bir açıklama sağlama açısından, testi anlamak için aşağıdakilere ihtiyaç vardır.
x ij = x + (x ben - x) + (x ij - x)
Bu, aşağıdaki modele götürür -
x ij = μ + α ben + ∈ ij
μ genel ortalama ve α i i . grup ortalamasıdır. Hata terimi ∈ ij varsayılır normal dağılımdan istatistiksel bağımsız olması. Testin boş hipotezi şudur:
α 1 = α 2 =… = α k
Test istatistiğini hesaplamak açısından, iki değeri hesaplamamız gerekiyor -
- Grup farkı için karelerin toplamı -
$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $$
- Gruplar içindeki karelerin toplamı
$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {ij}}} - \ bar {x _ {\ bar {i}}}) ^ 2 $$
SSD B'nin serbestlik derecesi k − 1 olduğu ve SSD W'nin serbestlik derecesi N − k olduğu yerlerde. Ardından, her bir metrik için ortalama kare farklarını tanımlayabiliriz.
MS B = SSD B / (k - 1)
MS ağırlık = SSD ağırlık / '- (N- k)
Son olarak, ANOVA'daki test istatistiği, yukarıdaki iki miktarın oranı olarak tanımlanır.
F = MS B / MS w
k − 1 ve N − k serbestlik dereceli bir F dağılımını takip eder. Boş hipotez doğruysa, F büyük olasılıkla 1'e yakın olacaktır. Aksi takdirde, gruplar arası ortalama kare MSB muhtemelen büyük olacaktır ve bu da büyük bir F değeriyle sonuçlanır.
Temel olarak, ANOVA toplam varyansın iki kaynağını inceler ve hangi kısmın daha fazla katkıda bulunduğunu görür. Bu nedenle, amaç grup ortalamalarını karşılaştırmak olsa da buna varyans analizi denir.
İstatistiği hesaplamak açısından, aslında R'de yapmak oldukça basittir. Aşağıdaki örnek, bunun nasıl yapıldığını gösterecek ve sonuçların grafiğini çizecektir.
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')Kod aşağıdaki çıktıyı üretecektir -

Örnekte elde ettiğimiz p değeri 0.05'ten önemli ölçüde daha küçüktür, bu nedenle R bunu belirtmek için '***' sembolünü döndürür. Bu, boş hipotezini reddettiğimiz ve mpg ortalamaları arasında farklı gruplar arasında farklılıklar bulduğumuz anlamına gelir.cyl değişken.