Büyük Veri Analitiği - Zaman Serisi Analizi

Zaman serisi, bir tarihe veya zaman damgasına göre indekslenmiş kategorik veya sayısal değişkenlerin gözlemleri dizisidir. Zaman serisi verilerinin açık bir örneği, hisse senedi fiyatının zaman serisidir. Aşağıdaki tabloda zaman serisi verilerinin temel yapısını görebiliriz. Bu durumda gözlemler her saat kaydedilir.

Zaman damgası	Hisse senedi fiyatı
2015-10-11 09:00:00	100
2015-10-11 10:00:00	110
2015-10-11 11:00:00	105
2015-10-11 12:00:00	90
2015-10-11 13:00:00	120

Normalde, zaman serisi analizinin ilk adımı seriyi çizmektir, bu normalde bir çizgi grafikle yapılır.

Zaman serisi analizinin en yaygın uygulaması, verilerin zamansal yapısını kullanarak sayısal bir değerin gelecekteki değerlerini tahmin etmektir. Bu, mevcut gözlemlerin gelecekteki değerleri tahmin etmek için kullanıldığı anlamına gelir.

Verilerin zamansal sıralaması, geleneksel regresyon yöntemlerinin kullanışlı olmadığı anlamına gelir. Sağlam bir tahmin oluşturmak için, verilerin zamansal sırasını hesaba katan modellere ihtiyacımız var.

Zaman Serisi Analizi için en yaygın kullanılan modele Autoregressive Moving Average(ARMA). Model iki bölümden oluşmaktadır:autoregressive (AR) bölümü ve bir moving average(MA) bölümü. Model genellikle daha sonra ARMA (p, q) modeli olarak adlandırılır , burada p otoregresif bölümün sırası ve q hareketli ortalama bölümün sırasıdır.

Otoregresif Model

AR (p) sipariş p bir kendiliğinden gerileyen modeli olarak okunur. Matematiksel olarak şöyle yazılır -

$$ X_t = c + \ sum_ {i = 1} ^ {P} \ phi_i X_ {t - i} + \ varepsilon_ {t} $$

burada {φ ₁ ,…, φ _p } tahmin edilecek parametrelerdir, c sabittir ve rastgele değişken ε _t beyaz gürültüyü temsil eder. Modelin sabit kalması için parametrelerin değerleri üzerinde bazı kısıtlamalar gereklidir.

Hareketli ortalama

Gösterimde MA (q) sipariş hareketli ortalama modeline değinmektedir q -

$$ X_t = \ mu + \ varepsilon_t + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {t - i} $$

θ ₁ , ..., θ _q modelin parametreleridir, μ X _t'nin beklentisidir ve ε _t , ε _{t - 1} , ... beyaz gürültü hatası terimleridir.

Otoregresif Hareketli Ortalama

ARMA (p, q) modeli birleştirir s kendiliğinden gerileyen koşulları ve q hareketli ortalama şartları. Matematiksel olarak model aşağıdaki formülle ifade edilir -

$$ X_t = c + \ varepsilon_t + \ sum_ {i = 1} ^ {P} \ phi_iX_ {t - 1} + \ sum_ {i = 1} ^ {q} \ theta_i \ varepsilon_ {ti} $$

Biz görebilirsiniz ARMA (p, q) modeli bir kombinasyonudur AR (p) ve MA (q) model.

Modelin bazı sezgi vermek denklemin AR parçası X için parametreleri tahmin etmeyi amaçlayan düşünün _{i - t} X değişkenin değerini tahmin etmek amacıyla gözlemlerini _t . Sonunda, geçmiş değerlerin ağırlıklı ortalamasıdır. MA bölümü aynı yaklaşımı kullanır, ancak önceki gözlemlerin hatasıyla, ε _{t - i} . Sonuç olarak, modelin sonucu ağırlıklı ortalamadır.

Aşağıdaki kod parçacığı , R'de bir ARMA'nın (p, q) nasıl uygulanacağını gösterir .

# install.packages("forecast")
library("forecast")  

# Read the data 
data = scan('fancy.dat') 
ts_data <- ts(data, frequency = 12, start = c(1987,1)) 
ts_data  
plot.ts(ts_data)

Verilerin grafiğini çizmek, normalde verilerde zamansal bir yapı olup olmadığını bulmak için ilk adımdır. Her yılın sonunda güçlü ani artışların olduğunu arsadan görebiliyoruz.

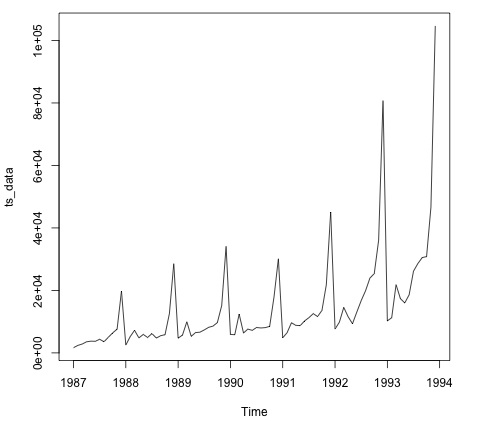
Aşağıdaki kod bir ARMA modelini verilere uyar. Birkaç model kombinasyonunu çalıştırır ve daha az hatası olanı seçer.

# Fit the ARMA model
fit = auto.arima(ts_data) 
summary(fit) 

# Series: ts_data  
# ARIMA(1,1,1)(0,1,1)[12]                     
#    Coefficients: 
#    ar1     ma1    sma1 
# 0.2401  -0.9013  0.7499 
# s.e.  0.1427   0.0709  0.1790 

#  
# sigma^2 estimated as 15464184:  log likelihood = -693.69 
# AIC = 1395.38   AICc = 1395.98   BIC = 1404.43 

# Training set error measures: 
#                 ME        RMSE      MAE        MPE        MAPE      MASE       ACF1 
# Training set   328.301  3615.374  2171.002  -2.481166  15.97302  0.4905797 -0.02521172