Sınıflandırma Algoritmaları - Karar Ağacı
Karar Ağacına Giriş
Genel olarak, Karar ağacı analizi birçok alanda uygulanabilen tahmine dayalı bir modelleme aracıdır. Karar ağaçları, veri setini farklı koşullara göre farklı şekillerde bölebilen algoritmik bir yaklaşımla oluşturulabilir. Karar bağları, denetimli algoritmalar kategorisine giren en güçlü algoritmalardır.
Hem sınıflandırma hem de regresyon görevleri için kullanılabilirler. Bir ağacın iki ana varlığı, verinin bölündüğü ve sonuç aldığımız yerde ayrıldığı karar düğümleridir. Yaş, yeme alışkanlıkları ve egzersiz alışkanlıkları gibi çeşitli bilgileri sağlayan bir kişinin formda olup olmadığını tahmin etmek için ikili ağaç örneği aşağıda verilmiştir -
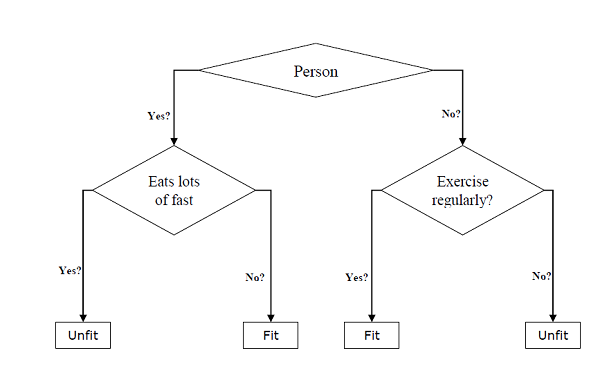
Yukarıdaki karar ağacında, soru karar düğümleridir ve nihai sonuçlar, yapraklardır. Aşağıdaki iki tür karar ağacına sahibiz -
Classification decision trees- Bu tür karar ağaçlarında karar değişkeni kategoriktir. Yukarıdaki karar ağacı, sınıflandırma karar ağacının bir örneğidir.
Regression decision trees - Bu tür karar ağaçlarında karar değişkeni süreklidir.
Karar Ağacı Algoritmasını Uygulama
Gini Endeksi
Veri kümesindeki ikili bölünmeleri değerlendirmek için kullanılan ve kategori hedef değişkeni "Başarı" veya "Başarısız" ile çalışan maliyet fonksiyonunun adıdır.
Gini indeksinin değeri ne kadar yüksekse, homojenlik o kadar yüksek olur. Mükemmel bir Gini indeksi değeri 0 ve en kötüsü 0.5'dir (2 sınıf problem için). Bölünme için Gini endeksi, aşağıdaki adımların yardımıyla hesaplanabilir -
İlk olarak, başarı ve başarısızlık olasılık karelerinin toplamı olan p ^ 2 + q ^ 2 formülünü kullanarak alt düğümler için Gini indeksini hesaplayın.
Ardından, bölünmenin her bir düğümünün ağırlıklı Gini puanını kullanarak bölünme için Gini endeksini hesaplayın.
Sınıflandırma ve Regresyon Ağacı (CART) algoritması, ikili bölünmeler oluşturmak için Gini yöntemini kullanır.
Bölünmüş Oluşturma
Bölme, temel olarak veri kümesine bir öznitelik ve bir değer içerir. Aşağıdaki üç bölümün yardımıyla veri kümesinde bir bölünme oluşturabiliriz -
Part1: Calculating Gini Score - Bu kısmı daha önceki bölümde tartışmıştık.
Part2: Splitting a dataset- Bir veri kümesini, bir özniteliğin indeksine ve bu özniteliğin bölünmüş değerine sahip iki satır listesine ayırmak olarak tanımlanabilir. Veri setinden sağ ve sol olmak üzere iki grubu aldıktan sonra, birinci bölümde hesaplanan Gini skorunu kullanarak bölünme değerini hesaplayabiliriz. Bölünmüş değer, özelliğin hangi grupta yer alacağına karar verir.
Part3: Evaluating all splits- Gini skorunu bulduktan ve veri setini ayırdıktan sonraki bölüm, tüm bölünmelerin değerlendirilmesidir. Bu amaçla, öncelikle her bir öznitelikle ilişkili her değeri bir aday bölünmesi olarak kontrol etmeliyiz. O halde, bölünmenin maliyetini değerlendirerek mümkün olan en iyi bölünmeyi bulmalıyız. En iyi ayrım, karar ağacında bir düğüm olarak kullanılacaktır.
Bir Ağaç Yapmak
Bir ağacın kök düğümü ve uç düğümleri olduğunu bildiğimiz gibi. Kök düğümü oluşturduktan sonra, iki bölümü izleyerek ağacı oluşturabiliriz -
Bölüm 1: Terminal düğümü oluşturma
Karar ağacının terminal düğümlerini oluştururken önemli bir nokta, ağacın büyümesinin ne zaman durdurulacağına veya başka terminal düğümlerinin oluşturulmasına karar vermektir. Maksimum ağaç derinliği ve minimum düğüm kayıtları olmak üzere iki kriter kullanılarak aşağıdaki şekilde yapılabilir -
Maximum Tree Depth- Adından da anlaşılacağı gibi, bu, kök düğümden sonra bir ağaçtaki maksimum düğüm sayısıdır. Bir ağaç maksimum derinliğe ulaştığında, yani bir ağaç maksimum sayıda terminal düğümüne ulaştığında, terminal düğümlerini eklemeyi bırakmalıyız.
Minimum Node Records- Belirli bir düğümün sorumlu olduğu minimum eğitim modeli sayısı olarak tanımlanabilir. Bu minimum düğüm kayıtlarında veya bu minimum değerin altında ağaca ulaşıldığında terminal düğümleri eklemeyi durdurmalıyız.
Son bir tahmin yapmak için terminal düğümü kullanılır.
Part2: Yinelemeli Bölme
Ne zaman terminal düğümleri oluşturacağımızı anladığımız için, şimdi ağacımızı oluşturmaya başlayabiliriz. Yinelemeli bölme, ağacı oluşturmak için bir yöntemdir. Bu yöntemde, bir düğüm oluşturulduktan sonra, aynı işlevi tekrar tekrar çağırarak, veri kümesini bölerek oluşturulan her veri grubu üzerinde özyinelemeli olarak çocuk düğümleri (mevcut bir düğüme eklenen düğümler) oluşturabiliriz.
Tahmin
Bir karar ağacı oluşturduktan sonra bunun hakkında bir tahmin yapmamız gerekiyor. Temel olarak tahmin, özel olarak sağlanan veri satırı ile karar ağacında gezinmeyi içerir.
Yukarıda olduğu gibi özyinelemeli fonksiyon yardımıyla bir tahmin yapabiliriz. Aynı tahmin rutini, sol veya alt sağ düğümlerle tekrar çağrılır.
Varsayımlar
Karar ağacını oluştururken yaptığımız varsayımlardan bazıları şunlardır -
Karar ağaçları hazırlanırken eğitim seti kök düğüm gibidir.
Karar ağacı sınıflandırıcısı, özellik değerlerinin kategorik olmasını tercih eder. Sürekli değerleri kullanmak istemeniz durumunda, model oluşturmadan önce bunların ayrı ayrı yapılması gerekir.
Özniteliğin değerlerine bağlı olarak kayıtlar yinelemeli olarak dağıtılır.
İstatistiksel yaklaşım, herhangi bir düğüm konumuna, yani kök düğüm veya dahili düğüm olarak öznitelikleri yerleştirmek için kullanılacaktır.
Python'da Uygulama
Misal
Aşağıdaki örnekte, Karar Ağacı sınıflandırıcısını Pima Indian Diabetes üzerinde uygulayacağız -
İlk olarak, gerekli python paketlerini içe aktararak başlayın -
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_splitArdından, iris veri kümesini web bağlantısından aşağıdaki şekilde indirin -
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1Şimdi, veri kümesini özelliklere ve hedef değişkene aşağıdaki gibi bölün -
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableDaha sonra, verileri tren ve test bölmesine ayıracağız. Aşağıdaki kod, veri kümesini% 70 eğitim verilerine ve test verilerinin% 30'una böler -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)Ardından, modeli DecisionTreeClassifier sklearn sınıfının yardımıyla aşağıdaki gibi eğitin -
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)Sonunda tahminde bulunmamız gerekiyor. Aşağıdaki komut dosyası yardımıyla yapılabilir -
y_pred = clf.predict(X_test)Ardından, doğruluk puanını, karışıklık matrisini ve sınıflandırma raporunu aşağıdaki gibi alabiliriz -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Çıktı
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671Karar Ağacını Görselleştirme
Yukarıdaki karar ağacı aşağıdaki kod yardımıyla görselleştirilebilir -
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())