Regresyon Algoritmaları - Doğrusal Regresyon
Doğrusal Regresyona Giriş
Doğrusal regresyon, bir bağımlı değişken ile verilen bağımsız değişkenler arasındaki doğrusal ilişkiyi analiz eden istatistiksel model olarak tanımlanabilir. Değişkenler arasındaki doğrusal ilişki, bir veya daha fazla bağımsız değişkenin değeri değiştiğinde (arttığında veya azaldığında), bağımlı değişkenin değerinin de buna göre değişeceği (artar veya azalır) anlamına gelir.
Matematiksel olarak ilişki, aşağıdaki denklem yardımı ile temsil edilebilir -
Y = mX + b
Burada Y, tahmin etmeye çalıştığımız bağımlı değişkendir
X , tahmin yapmak için kullandığımız bağımlı değişkendir.
m , X'in Y üzerindeki etkisini temsil eden regresyon doğrusunun eğimidir.
b , Y kesme noktası olarak bilinen bir sabittir. X = 0 ise, Y b'ye eşit olacaktır.
Ayrıca, doğrusal ilişki, aşağıda açıklandığı gibi doğası gereği olumlu veya olumsuz olabilir -
Pozitif Doğrusal İlişki
Hem bağımsız hem de bağımlı değişken artarsa, doğrusal bir ilişki pozitif olarak adlandırılacaktır. Aşağıdaki grafiğin yardımıyla anlaşılabilir -

Negatif Doğrusal ilişki
Bağımsız artarsa ve bağımlı değişken azalırsa doğrusal bir ilişki pozitif olarak adlandırılacaktır. Aşağıdaki grafiğin yardımıyla anlaşılabilir -

Doğrusal Regresyon Türleri
Doğrusal regresyon aşağıdaki iki türdendir -
- Basit Doğrusal Regresyon
- Çoklu doğrusal regresyon
Basit Doğrusal Regresyon (SLR)
Tek bir özelliği kullanarak bir yanıtı öngören doğrusal regresyonun en temel versiyonudur. SLR'deki varsayım, iki değişkenin doğrusal olarak ilişkili olmasıdır.
Python uygulaması
SLR'yi Python'da iki şekilde uygulayabiliriz, biri kendi veri kümenizi sağlamak, diğeri scikit-learn python kitaplığındaki veri kümesini kullanmaktır.
Example 1 Aşağıdaki Python uygulama örneğinde, kendi veri setimizi kullanıyoruz.
İlk olarak, aşağıdaki gibi gerekli paketleri içe aktarmaya başlayacağız -
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltArdından, SLR için önemli değerleri hesaplayacak bir işlev tanımlayın -
def coef_estimation(x, y):Aşağıdaki kod satırı, gözlemlerin sayısını verecektir n -
n = np.size(x)X ve y vektörlerinin ortalaması aşağıdaki gibi hesaplanabilir -
m_x, m_y = np.mean(x), np.mean(y)X ile ilgili çapraz sapma ve sapmayı aşağıdaki gibi bulabiliriz -
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xDaha sonra, regresyon katsayıları, yani b aşağıdaki gibi hesaplanabilir -
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Daha sonra, regresyon çizgisini çizecek ve yanıt vektörünü tahmin edecek bir fonksiyon tanımlamamız gerekiyor -
def plot_regression_line(x, y, b):Aşağıdaki komut dosyası satırı, gerçek noktaları dağılım grafiği olarak çizecektir -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Aşağıdaki komut dosyası satırı yanıt vektörünü tahmin edecektir -
y_pred = b[0] + b[1]*xAşağıdaki betik satırları regresyon çizgisini çizecek ve etiketleri üzerlerine koyacaktır -
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Sonunda, veri kümesi sağlamak ve yukarıda tanımladığımız işlevi çağırmak için main () işlevini tanımlamamız gerekiyor -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Çıktı
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788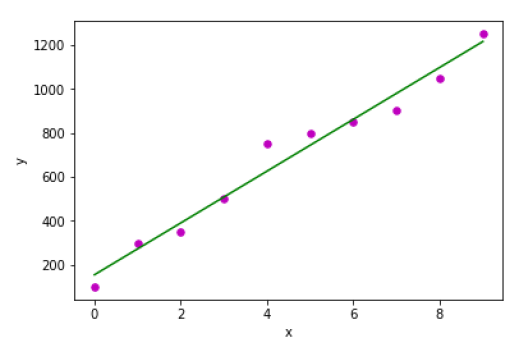
Example 2 Aşağıdaki Python uygulama örneğinde, scikit-learn'den diyabet veri kümesini kullanıyoruz.
İlk olarak, aşağıdaki gibi gerekli paketleri içe aktarmaya başlayacağız -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreDaha sonra, diyabet veri setini yükleyeceğiz ve nesnesini oluşturacağız -
diabetes = datasets.load_diabetes()SLR'yi uygularken, aşağıdaki gibi yalnızca bir özellik kullanacağız -
X = diabetes.data[:, np.newaxis, 2]Ardından, verileri aşağıdaki gibi eğitim ve test setlerine bölmemiz gerekiyor -
X_train = X[:-30]
X_test = X[-30:]Ardından, hedefi eğitim ve test setlerine aşağıdaki gibi bölmemiz gerekiyor -
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Şimdi, modeli eğitmek için aşağıdaki gibi doğrusal regresyon nesnesi oluşturmamız gerekiyor -
regr = linear_model.LinearRegression()Ardından, modeli eğitim setlerini kullanarak aşağıdaki gibi eğitin -
regr.fit(X_train, y_train)Ardından, test setini kullanarak aşağıdaki gibi tahminler yapın -
y_pred = regr.predict(X_test)Ardından, MSE, Varyans skoru vb. Gibi bazı katsayıları aşağıdaki gibi yazdıracağız -
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Şimdi çıktıları aşağıdaki gibi çizin -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Çıktı
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Çoklu Doğrusal Regresyon (MLR)
İki veya daha fazla özelliği kullanarak bir yanıtı tahmin eden basit doğrusal regresyonun uzantısıdır. Matematiksel olarak bunu şu şekilde açıklayabiliriz -
N gözlem, p özellikleri, yani bağımsız değişkenler ve y tek yanıt, yani bağımlı değişken içeren bir veri setini düşünün, p özellikleri için regresyon çizgisi aşağıdaki gibi hesaplanabilir -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$Burada, h (x i ) tahmin edilen yanıt değeridir ve b 0 , b 1 , b 2 …, b p regresyon katsayılarıdır.
Çoklu Doğrusal Regresyon modelleri, her zaman, hesaplamayı aşağıdaki gibi değiştiren artık hata olarak bilinen verilerdeki hataları içerir -
$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$Yukarıdaki denklemi şu şekilde de yazabiliriz -
$$ y_ {i} = h (x_ {i}) + e_ {i} \: veya \: e_ {i} = y_ {i} - h (x_ {i}) $$Python Uygulaması
bu örnekte, scikit learn'den Boston konut veri kümesini kullanacağız -
İlk olarak, aşağıdaki gibi gerekli paketleri içe aktarmaya başlayacağız -
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsArdından, veri kümesini aşağıdaki gibi yükleyin -
boston = datasets.load_boston(return_X_y=False)Aşağıdaki kod satırları özellik matrisi, X ve yanıt vektörü Y'yi tanımlayacaktır -
X = boston.data
y = boston.targetArdından, veri kümesini eğitim ve test kümelerine aşağıdaki şekilde bölün:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Misal
Şimdi, doğrusal regresyon nesnesi oluşturun ve modeli aşağıdaki gibi eğitin -
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Çıktı
Coefficients:
[
-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01
]
Variance score: 0.709454060230326
Varsayımlar
Aşağıdakiler, Doğrusal Regresyon modeli tarafından yapılan veri kümesiyle ilgili bazı varsayımlardır -
Multi-collinearity- Doğrusal regresyon modeli, verilerde çok az çoklu doğrusallık olduğunu veya hiç olmadığını varsayar. Temel olarak, çoklu doğrusallık, bağımsız değişkenler veya özellikler içlerinde bağımlılığa sahip olduğunda ortaya çıkar.
Auto-correlation- Doğrusal regresyon modelinin varsaydığı başka bir varsayım, verilerde çok az veya hiç oto-korelasyon olduğunu varsayar. Temel olarak, otomatik korelasyon, artık hatalar arasında bağımlılık olduğunda ortaya çıkar.
Relationship between variables - Doğrusal regresyon modeli, yanıt ve özellik değişkenleri arasındaki ilişkinin doğrusal olması gerektiğini varsayar.