Sınıflandırma Algoritmaları - Lojistik Regresyon
Lojistik Regresyona Giriş
Lojistik regresyon, bir hedef değişkenin olasılığını tahmin etmek için kullanılan denetimli bir öğrenme sınıflandırma algoritmasıdır. Hedef veya bağımlı değişkenin doğası ikiye bölünmüştür, bu da yalnızca iki olası sınıf olacağı anlamına gelir.
Basit bir deyişle, bağımlı değişken, doğası gereği, verileri 1 (başarı / evet anlamına gelir) veya 0 (başarısızlık / hayır anlamına gelir) olarak kodlanmış olan ikilidir.
Matematiksel olarak, bir lojistik regresyon modeli, P'yi (Y = 1) X'in bir fonksiyonu olarak öngörür. İstenmeyen posta tespiti, Diyabet tahmini, kanser tespiti gibi çeşitli sınıflandırma problemleri için kullanılabilen en basit ML algoritmalarından biridir.
Lojistik Regresyon Türleri
Genel olarak, lojistik regresyon, ikili hedef değişkenlere sahip ikili lojistik regresyon anlamına gelir, ancak bunun tarafından tahmin edilebilecek iki hedef değişken kategorisi daha olabilir. Bu kategori sayısına bağlı olarak, Lojistik regresyon aşağıdaki türlere ayrılabilir -
İkili veya Binom
Bu tür bir sınıflandırmada, bağımlı bir değişkenin 1 ve 0 olmak üzere yalnızca iki olası türü olacaktır. Örneğin, bu değişkenler başarı veya başarısızlığı, evet veya hayır, kazanma veya kaybı vb. Temsil edebilir.
Çok terimli
Bu tür bir sınıflandırmada, bağımlı değişken 3 veya daha fazla olası sırasız türe sahip olabilir veya nicel önemi olmayan türler olabilir. Örneğin, bu değişkenler "Tip A" veya "Tip B" veya "Tip C" yi temsil edebilir.
Sıra
Bu tür bir sınıflandırmada, bağımlı değişken 3 veya daha fazla olası sıralı türe veya niceliksel önemi olan tiplere sahip olabilir. Örneğin, bu değişkenler "zayıf" veya "iyi", "çok iyi", "Mükemmel" i temsil edebilir ve her kategori 0,1,2,3 gibi puanlara sahip olabilir.
Lojistik Regresyon Varsayımları
Lojistik regresyon uygulamasına dalmadan önce, aynı şeyle ilgili aşağıdaki varsayımların farkında olmalıyız:
İkili lojistik regresyon durumunda, hedef değişkenler her zaman ikili olmalıdır ve istenen sonuç faktör seviyesi 1 ile temsil edilir.
Modelde çoklu doğrusallık olmamalıdır, bu da bağımsız değişkenlerin birbirinden bağımsız olması gerektiği anlamına gelir.
Modelimize anlamlı değişkenler eklemeliyiz.
Lojistik regresyon için büyük bir örneklem büyüklüğü seçmeliyiz.
İkili Lojistik Regresyon modeli
Lojistik regresyonun en basit şekli, hedef veya bağımlı değişkenin 1 veya 0 olmak üzere yalnızca 2 olası tipine sahip olabileceği ikili veya iki terimli lojistik regresyondur. Bu, birden çok öngörücü değişken ile ikili / iki terimli bir hedef değişken arasındaki bir ilişkiyi modellememize olanak tanır. Lojistik regresyon durumunda, doğrusal fonksiyon temelde aşağıdaki ilişki gibi başka bir fonksiyona girdi olarak kullanılır -
$$ h _ {\ theta} {(x)} = g (\ theta ^ {T} x) ℎ 0≤h _ {\ theta} ≤1 $$İşte aşağıdaki gibi verilebilen lojistik veya sigmoid fonksiyondur -
$$ g (z) = \ frac {1} {1 + e ^ {- z}} ℎ = \ theta ^ {T} $$Sigmoid eğrisine aşağıdaki grafik yardımı ile gösterilebilir. Y ekseninin değerlerinin 0 ile 1 arasında olduğunu ve ekseni 0,5'te geçtiğini görebiliriz.

Sınıflar olumlu veya olumsuz olarak ayrılabilir. Çıktı 0 ile 1 arasındaysa pozitif sınıf olasılığının altına gelir. Uygulamamız için, hipotez fonksiyonunun çıktısını ≥0,5 ise pozitif, aksi takdirde negatif olarak yorumluyoruz.
Ayrıca, algoritmanın işlevler üzerindeki ağırlıkları kullanarak ne kadar iyi performans gösterdiğini ölçmek için aşağıdaki gibi teta ile gösterilen bir kayıp işlevi tanımlamamız gerekir -
ℎ = ()
$$ J (\ theta) = \ frac {1} {m}. (- y ^ {T} log (h) - (1 -y) ^ Tlog (1-h)) $$Şimdi, kayıp fonksiyonunu tanımladıktan sonra birincil hedefimiz kayıp fonksiyonunu en aza indirmektir. Ağırlıkların artırılması veya azaltılması anlamına gelen ağırlıkların takılması yardımı ile yapılabilir. Her bir ağırlıktaki kayıp fonksiyonunun türevlerinin yardımıyla hangi parametrelerin yüksek ağırlığa ve neyin daha küçük ağırlığa sahip olması gerektiğini bilebilirdik.
Aşağıdaki gradyan iniş denklemi, parametreleri değiştirirsek kaybın nasıl değişeceğini anlatır -
$$ \ frac {()} {\ theta_ {j}} = \ frac {1} {m} X ^ {T} (() -) $$Python'da Uygulama
Şimdi Python'da yukarıdaki binom lojistik regresyon kavramını uygulayacağız. Bu amaçla, her biri 50 örnekten oluşan 3 sınıfa sahip 'iris' adlı çok değişkenli bir çiçek veri kümesi kullanıyoruz, ancak ilk iki özellik sütununu kullanacağız. Her sınıf bir tür iris çiçeğini temsil eder.
Öncelikle, gerekli kitaplıkları aşağıdaki gibi içe aktarmamız gerekiyor -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasetsArdından, iris veri kümesini aşağıdaki gibi yükleyin -
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1Eğitim verilerimizi aşağıdaki şekilde çizebiliriz -
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();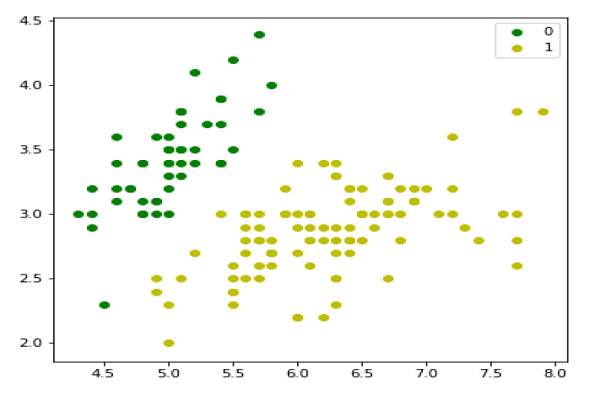
Ardından, sigmoid fonksiyonunu, kayıp fonksiyonunu ve gradyan inişini aşağıdaki gibi tanımlayacağız -
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)Şimdi ağırlıkları aşağıdaki gibi başlatın -
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')Aşağıdaki betik yardımıyla çıktı olasılıklarını tahmin edebiliriz -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()Ardından, modeli değerlendirip aşağıdaki gibi çizebiliriz -
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
Çok Terimli Lojistik Regresyon Modeli
Lojistik regresyonun diğer bir kullanışlı formu, hedef veya bağımlı değişkenin 3 veya daha fazla olası sırasız tipe, yani niceliksel önemi olmayan tiplere sahip olabileceği multinomial lojistik regresyondur.
Python'da Uygulama
Şimdi Python'da yukarıdaki çok terimli lojistik regresyon kavramını uygulayacağız. Bu amaçla sklearn isimli digit'den bir veri seti kullanıyoruz.
Öncelikle, gerekli kitaplıkları aşağıdaki gibi içe aktarmamız gerekiyor -
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_splitSonra, rakam veri setini yüklememiz gerekiyor -
digits = datasets.load_digits()Şimdi, özellik matrisini (X) ve yanıt vektörünü (y) aşağıdaki gibi tanımlayın -
X = digits.data
y = digits.targetBir sonraki kod satırının yardımıyla, X ve y'yi eğitim ve test setlerine ayırabiliriz -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)Şimdi aşağıdaki gibi bir lojistik regresyon nesnesi oluşturun -
digreg = linear_model.LogisticRegression()Şimdi, aşağıdaki eğitim setlerini kullanarak modeli eğitmemiz gerekiyor -
digreg.fit(X_train, y_train)Ardından, test setiyle ilgili tahminleri aşağıdaki gibi yapın -
y_pred = digreg.predict(X_test)Daha sonra modelin doğruluğunu aşağıdaki gibi yazdırın -
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)Çıktı
Accuracy of Logistic Regression model is: 95.6884561891516Yukarıdaki çıktıdan modelimizin doğruluğunun yüzde 96 civarında olduğunu görebiliyoruz.