Radar Sistemleri - Gecikme Hattı İptalleri
Bu bölümde, Radar Sistemlerinde Gecikme Hattı İptal Ediciler hakkında bilgi edineceğiz. Adından da anlaşılacağı gibi, gecikme çizgisi belirli bir miktarda gecikme getirir. Bu nedenle, gecikme hattı esas olarak Gecikme hattı iptalinde kullanılır.delay nabız tekrarlama süresi.
Delay line cancellersabit hedeflerden alınan eko sinyallerinin DC bileşenlerini ortadan kaldıran bir filtredir. Bu, sabit olmayan hedeflerden, yani hareketli hedeflerden alınan eko sinyallerinin AC bileşenlerine izin verdiği anlamına gelir.
Gecikme Hattı İptali Türleri
Gecikme hattı iptalleri aşağıdaki şekilde sınıflandırılabilir two types içinde bulunan gecikme hatlarının sayısına göre.
- Tek Gecikmeli Hat İptali
- Çift Gecikmeli Hat İptali
Sonraki bölümlerimizde, bu iki Gecikme hattı iptalcisi hakkında daha fazla tartışacağız.
Tek Gecikmeli Hat İptali
Bir gecikme hattı ve bir çıkarıcı kombinasyonu, Gecikme hattı iptali olarak bilinir. Tek Gecikmeli hat iptalcisi olarak da adlandırılır. block diagram Tek Gecikme hattı iptalcisine sahip MTI alıcısı aşağıdaki şekilde gösterilmektedir.
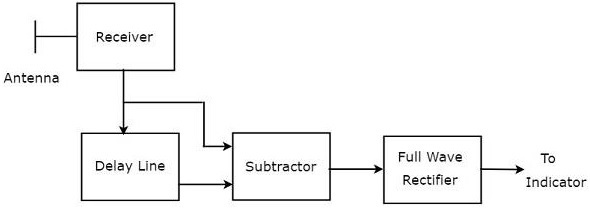
Biz yazabiliriz mathematical equation Doppler etkisinden sonra alınan yankı sinyalinin -
$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:Equation\:1$$
Nerede,
A, video sinyalinin genliğidir
$f_d$ Doppler frekansıdır
$\phi_o$ faz kaymasıdır ve eşittir $4\pi f_tR_o/C$
Alacağız output of Delay line canceller, değiştirerek $t$ tarafından $t-T_P$ Denklem 1'de.
$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:Equation\:2$$
Nerede,
$T_P$ nabız tekrarlama zamanı
Alacağız subtractor output Denklem 2'yi Denklem 1'den çıkararak.
$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$
$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$
$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$
$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:Equation\:3$$
Çıkarıcı çıktısı Tam Dalga Doğrultucuya girdi olarak uygulanır. Bu nedenle, Tam Dalga Doğrultucunun çıkışı aşağıdaki şekilde gösterildiği gibi görünür. Başka bir şey değilfrequency response Tek gecikme hattı iptalcisinin.

Denklem 3'ten, tek gecikme hattı iptalcisinin frekans cevabının sıfır olduğunu gözlemleyebiliriz. $\pi f_dT_P$ eşittir integer multiples of $\pi$ Bunun anlamı, $\pi f_dT_P$ eşittir $n\pi$ Matematiksel olarak şu şekilde yazılabilir:
$$\pi f_dT_P=n\pi$$
$$\Rightarrow f_dT_P=n$$
$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:Equation\:4$$
Denklem 4'ten, Doppler frekansı olduğunda, tek gecikme hattı iptal edicisinin frekans yanıtının sıfır olduğu sonucuna varabiliriz. $f_d$ darbe tekrarlama süresinin tersinin tam sayı katlarına eşittir $T_P$.
Darbe tekrarlama süresi ile darbe tekrarlama frekansı arasında aşağıdaki ilişkiyi biliyoruz.
$$f_d=\frac{1}{T_P}$$
$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:Equation\:5$$
Denklem 4'teki Denklem 5'i değiştirerek aşağıdaki denklemi elde edeceğiz.
$$\Rightarrow f_d=nf_P\:\:\:\:\:Equation\:6$$
Denklem 6'dan, Doppler frekansı, tek gecikme hattı iptal edicisinin frekans yanıtının sıfır olduğu sonucuna varabiliriz. $f_d$ darbe tekrarlama frekansının tam sayı katlarına eşittir $f_P$.
Kör Hızlar
Şimdiye kadar öğrendiklerimizden, tek Gecikme hattı iptali, sabit hedeflerden alınan yankı sinyallerinin DC bileşenlerini ortadan kaldırır. $n$sıfıra eşittir. Buna ek olarak, Doppler frekansı olduğunda sabit olmayan hedeflerden alınan yankı sinyallerinin AC bileşenlerini de ortadan kaldırır.$f_d$ tam sayıya eşittir (other than zero) darbe tekrarlama frekansının katları $f_P$.
Bu nedenle, tek gecikme hattı iptalcisinin frekans cevabının sıfır olduğu göreceli hızlar denir. blind speeds. Matematiksel olarak, kör hız ifadesini yazabiliriz$v_n$ olarak -
$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:Equation\:7$$
$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:Equation\:8$$
Nerede,
$n$ bir tamsayıdır ve 1, 2, 3'e eşittir vb.
$\lambda$ çalışma dalga boyu
Örnek Problem
Bir MTI Radar aşağıdaki frekanslarda çalışır: $6GHZ$ darbe tekrarlama frekansı ile $1KHZ$. Birinci, ikinci ve üçüncüyü bulunblind speeds Bu Radar.
Çözüm
Verilen,
MTI Radarın çalışma frekansı, $f=6GHZ$
Darbe tekrarlama frekansı, $f_P=1KHZ$.
Aşağıdaki formül şu şekildedir: operating wavelength $\lambda$ çalışma frekansı açısından, f.
$$\lambda=\frac{C}{f}$$
Vekil, $C=3\times10^8m/sec$ ve $f=6GHZ$ yukarıdaki denklemde.
$$\lambda=\frac{3\times10^8}{6\times10^9}$$
$$\Rightarrow \lambda=0.05m$$
Böylece operating wavelength $\lambda$ eşittir $0.05m$, çalışma frekansı f olduğunda $6GHZ$.
Aşağıdakileri biliyoruz formula for blind speed.
$$v_n=\frac{n\lambda f_p}{2}$$
İkame ederek, $n$= 1,2 & 3 yukarıdaki denklemde, sırasıyla birinci, ikinci ve üçüncü kör hızlar için aşağıdaki denklemleri alacağız.
$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$
$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$
$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$
Substitute değerleri $\lambda$ ve $f_P$ ilk kör hız denkleminde.
$$v_1=\frac{0.05\times 10^3}{2}$$
$$\Rightarrow v_1=25m/sec$$
bu yüzden first blind speed $v_1$ eşittir $25m/sec$ verilen özellikler için.
Değerlerini alacağız second & third blind speeds gibi $50m/sec$& $75m/sec$ sırasıyla ikinci ve üçüncü kör hız denklemlerinde 1 değerini değiştirerek.
Çift Gecikmeli Hat İptali
Tek bir gecikme hattı iptal edicisinin bir gecikme hattı ve bir çıkarıcıdan oluştuğunu biliyoruz. Bu tür iki gecikme hattı iptal edicisi birlikte kademeli olarak bağlanırsa, bu kombinasyona Çift gecikmeli hat iptalcisi denir. block diagram Çift gecikmeli hat iptali aşağıdaki şekilde gösterilmiştir.

İzin Vermek $p\left ( t \right )$ ve $q\left ( t \right )$ilk gecikme hattı iptalcisinin girişi ve çıkışı olabilir. Aşağıdaki matematiksel ilişkiyi alacağızfirst delay line canceller.
$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:Equation\:9$$
Birinci gecikme hattı iptal edicisinin çıkışı, ikinci gecikme hattı iptal edicisine bir girdi olarak uygulanır. Bu nedenle$q\left ( t \right )$ikinci gecikme hattı iptal edicisinin girişi olacaktır. İzin Vermek$r\left ( t \right )$ikinci gecikme hattı iptalcisinin çıkışı olabilir. Aşağıdaki matematiksel ilişkiyisecond delay line canceller.
$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:Equation\:10$$
Değiştir $t$ tarafından $t-T_P$ Denklem 9'da.
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:Equation\:11$$
SubstituteDenklem 10'daki Denklem 9 ve Denklem 11.
$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$
$$\Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:Equation\:12$$
advantageÇift gecikmeli hat iptali, dağınıklığı geniş ölçüde reddetmesidir. Basamaklı olan iki gecikme hattı iptalcisinin çıkışı, tek gecikme hattı iptalcisinin çıktısının karesine eşit olacaktır.
Dolayısıyla, MTI Radar alıcısında bulunan çift gecikmeli hat iptalinin çıktısının büyüklüğü şuna eşit olacaktır. $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$.

Hem çift gecikmeli hat iptalinin hem de iki gecikme hattı iptal edicisinin kademeli kombinasyonunun frekans yanıtı özellikleri aynıdır. advantage Zaman etki alanı gecikmeli hat iptalcilerinin bir kısmı, tüm frekans aralıkları için çalıştırılabilmesidir.