Grundlegende Elektronik - Transformatoren
Nach dem Prinzip von Electromagnetic InductionWir haben bereits gelernt, dass ein variierender Fluss eine EMF in einer Spule induzieren kann. Nach dem Prinzip vonMutual inductionWenn eine andere Spule neben eine solche Spule gebracht wird, induziert der Fluss EMF in die zweite Spule.
Nun wird die Spule, die den variierenden Fluss hat, als die bezeichnet Primary Coil und die Spule, in die EMF induziert wird, wird als die bezeichnet Secondary Coil, während die beiden Spulen zusammen eine Einheit bilden, die als a bezeichnet wird Transformer.
Transformator
Ein Transformator hat eine Primärspule, zu der der Eingang gegeben ist, und eine Sekundärspule, von der der Ausgang gesammelt wird. Beide Spulen sind auf ein Kernmaterial gewickelt. In der Regel bildet ein Isolator dieCore des Transformators.
Die folgende Abbildung zeigt einen praktischen Transformator.
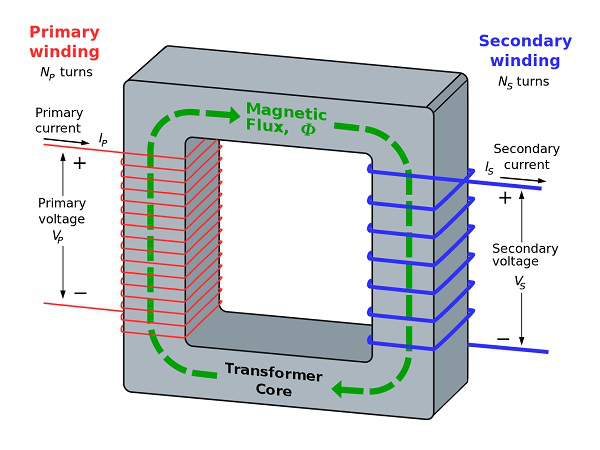
Aus der obigen Abbildung ist ersichtlich, dass nur wenige Notationen üblich sind. Lassen Sie uns versuchen, eine Notiz von ihnen zu haben. Sie sind -
Np = Anzahl der Windungen in der Primärwicklung
Ns = Anzahl der Windungen in der Sekundärwicklung
Ip = Strom fließt in der Primärwicklung des Transformators
Is = Strom fließt in der Sekundärseite des Transformators
Vp = Spannung an der Primärseite des Transformators
Vs = Spannung an der Sekundärseite des Transformators
Φ = Magnetfluss um den Kern des Transformators.
Transformator in einem Stromkreis
Die folgende Abbildung zeigt, wie ein Transformator in einer Schaltung dargestellt wird. Die Primärwicklung, die Sekundärwicklung und der Kern des Transformators sind ebenfalls in der folgenden Abbildung dargestellt.
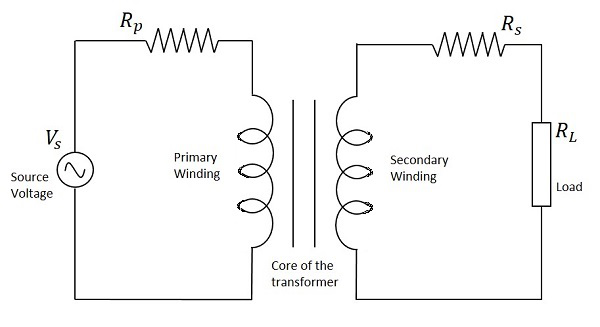
Wenn also ein Transformator in einen Stromkreis geschaltet wird, wird die Eingangsversorgung der Primärspule gegeben, so dass sie mit dieser Stromversorgung einen variierenden Magnetfluss erzeugt und dieser Fluss in die Sekundärspule des Transformators induziert wird, der die variierende EMF von erzeugt der variierende Fluss. Da der Fluss variieren sollte, arbeitet ein Transformator für die Übertragung von EMF von primär zu sekundär immer mit Wechselstrom.
Step-up und Step-down
Abhängig von der Anzahl der Windungen in der Sekundärwicklung kann der Transformator als a bezeichnet werden Step up oder ein Step down Transformator.
Der wichtigste Punkt, der hier zu beachten ist, ist, dass es keinen Unterschied zwischen dem primären und dem sekundären gibt powerdes Transformators. Wenn dementsprechend die Spannung an der Sekundärseite hoch ist, wird ein niedriger Strom gezogen, um die Leistung stabil zu machen. Wenn die Spannung in der Sekundärseite niedrig ist, wird auch ein hoher Strom gezogen, so dass die Leistung der Primärseite entsprechen muss.
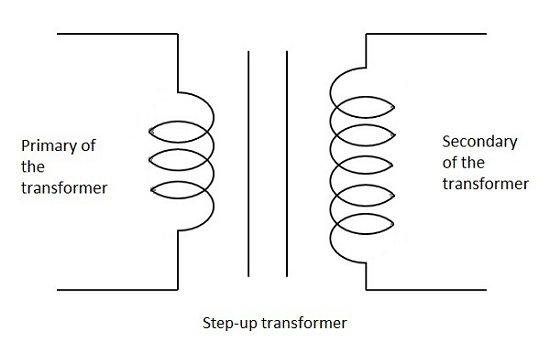
Steigern Sie
Wenn die Sekundärwicklung mehr Windungen als die Primärwicklung hat, wird der Transformator als a bezeichnet Step-upTransformator. Hier ist die induzierte EMF größer als das Eingangssignal.
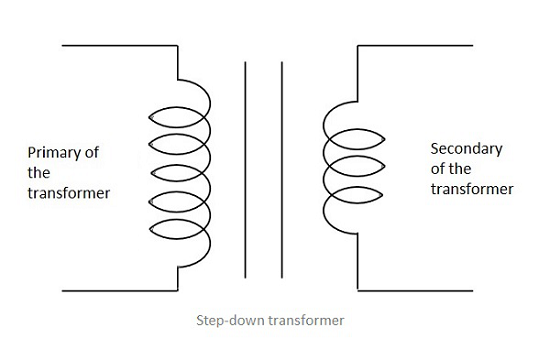
Schritt zurück
Wenn die Sekundärwicklung weniger Windungen hat als die Primärwicklung, wird der Transformator als a bezeichnet Step-downTransformator. Hier ist die induzierte EMF geringer als das Eingangssignal.
Drehverhältnis
Da die Anzahl der Windungen der Primär- und Sekundärwicklung die Nennspannung beeinflusst, ist es wichtig, ein Verhältnis zwischen den Windungen einzuhalten, um eine Vorstellung von den induzierten Spannungen zu haben.
Das Verhältnis der Windungszahl in der Primärspule zur Windungszahl in der Sekundärspule wird als „turns ratio" oder "the ratio of transformation”. Das Windungsverhältnis wird üblicherweise mit bezeichnetN.
$$ N \: \: = \: \: Turns \: ratio \: \: = \: \: \ frac {Anzahl \: von \: Turns \: on \: Primary} {Anzahl \: von \: Turns \: on \: Secondary} \: \: = \: \: \ frac {N_ {p}} {N_ {s}} $$
Das Verhältnis von Primär zu Sekundär, das Verhältnis von Eingang zu Ausgang und das Windungsverhältnis eines bestimmten Transformators sind dieselben wie sein voltage ratio. Daher kann dies geschrieben werden als
$$ \ frac {N_ {p}} {N_ {s}} \: \: = \: \: \ frac {V_ {p}} {V_ {s}} \: \: = \: \: N \ : \: = \: \: Turns \: ratio $$
Das Windungsverhältnis gibt auch an, ob der Transformator ein Aufwärts- oder ein Abwärtstransformator ist. Beispielsweise gibt ein Windungsverhältnis von 1: 3 an, dass der Transformator ein Aufwärtstransformator ist, und das Verhältnis 3: 1 besagt, dass es sich um einen Abwärtstransformator handelt.