DAA - Binärer Haufen

Es gibt verschiedene Arten von Heaps. In diesem Kapitel werden wir jedoch auf binäre Heaps eingehen. EINbinary heapist eine Datenstruktur, die einem vollständigen Binärbaum ähnelt. Die Heap-Datenstruktur entspricht den unten beschriebenen Reihenfolgeeigenschaften. Im Allgemeinen wird ein Heap durch ein Array dargestellt. In diesem Kapitel stellen wir einen Haufen von darH.

Da die Elemente eines Heaps in einem Array gespeichert sind, wird der Startindex als betrachtet 1, die Position des Elternknotens von i^th Element finden Sie unter ⌊ i/2 ⌋. Linkes Kind und rechtes Kind voni^th Knoten ist an Position 2i und 2i + 1.

Ein binärer Heap kann weiter als entweder a klassifiziert werden max-heap oder ein min-heap basierend auf der bestellenden Eigenschaft.

Max-Heap

In diesem Heap ist der Schlüsselwert eines Knotens größer oder gleich dem Schlüsselwert des höchsten untergeordneten Knotens.

Daher, H[Parent(i)] ≥ H[i]

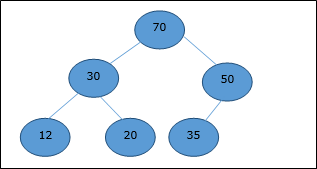
Min-Heap

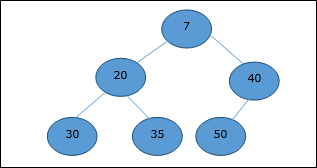
Im Mittelwert-Heap ist der Schlüsselwert eines Knotens kleiner oder gleich dem Schlüsselwert des niedrigsten untergeordneten Elements.

Daher, H[Parent(i)] ≤ H[i]

In diesem Zusammenhang werden nachfolgend grundlegende Operationen in Bezug auf Max-Heap gezeigt. Das Einfügen und Löschen von Elementen in und aus Haufen erfordert eine Neuanordnung von Elementen. Daher,Heapify Funktion muss aufgerufen werden.

Array-Darstellung

Ein vollständiger Binärbaum kann durch ein Array dargestellt werden, in dem seine Elemente mithilfe der Durchquerung der Ebenenreihenfolge gespeichert werden.

Betrachten wir einen Heap (wie unten gezeigt), der durch ein Array dargestellt wird H.

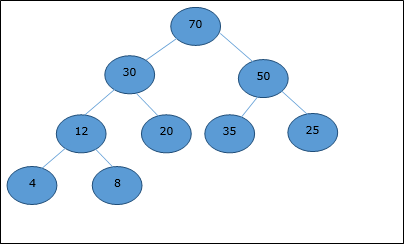
Betrachtet man den Startindex als 0Bei Verwendung der Durchquerung der Ebenenreihenfolge werden die Elemente wie folgt in einem Array gehalten.

Index	0	1	2	3	4	5	6	7	8	...
elements	70	30	50	12	20	35	25	4	8	...

In diesem Zusammenhang werden Operationen auf dem Heap in Bezug auf Max-Heap dargestellt.

So finden Sie den Index des übergeordneten Elements eines Elements unter index i, der folgende Algorithmus Parent (numbers[], i) wird eingesetzt.

Algorithm: Parent (numbers[], i) 
if i == 1 
   return NULL 
else 
   [i / 2]

Der Index des linken untergeordneten Elements eines Elements am Index i kann mit dem folgenden Algorithmus gefunden werden: Left-Child (numbers[], i).

Algorithm: Left-Child (numbers[], i) 
If 2 * i ≤ heapsize 
   return [2 * i] 
else 
   return NULL

Der Index des rechten untergeordneten Elements eines Elements am Index i kann mit dem folgenden Algorithmus gefunden werden: Right-Child(numbers[], i).

Algorithm: Right-Child (numbers[], i) 
if 2 * i < heapsize 
   return [2 * i + 1] 
else 
   return NULL