DAA - Sortierung zusammenführen
In diesem Kapitel werden wir die Zusammenführungssortierung diskutieren und ihre Komplexität analysieren.
Problemstellung
Das Problem des Sortierens einer Liste von Zahlen bietet sich sofort für eine Divide-and-Conquer-Strategie an: Teilen Sie die Liste in zwei Hälften, sortieren Sie jede Hälfte rekursiv und führen Sie dann die beiden sortierten Unterlisten zusammen.
Lösung
Bei diesem Algorithmus werden die Zahlen in einem Array gespeichert numbers[]. Hier,p und q repräsentiert den Start- und Endindex eines Subarrays.
Algorithm: Merge-Sort (numbers[], p, r)
if p < r then
q = ⌊(p + r) / 2⌋
Merge-Sort (numbers[], p, q)
Merge-Sort (numbers[], q + 1, r)
Merge (numbers[], p, q, r)Function: Merge (numbers[], p, q, r)
n1 = q – p + 1
n2 = r – q
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays
for i = 1 to n1
leftnums[i] = numbers[p + i - 1]
for j = 1 to n2
rightnums[j] = numbers[q+ j]
leftnums[n1 + 1] = ∞
rightnums[n2 + 1] = ∞
i = 1
j = 1
for k = p to r
if leftnums[i] ≤ rightnums[j]
numbers[k] = leftnums[i]
i = i + 1
else
numbers[k] = rightnums[j]
j = j + 1Analyse
Betrachten wir die Laufzeit von Merge-Sort als T(n). Daher,
$ T (n) = \ begin {Fälle} c & if \: n \ leqslant 1 \\ 2 \: x \: T (\ frac {n} {2}) + d \: x \: n & sonst \ ende {Fälle} $ wobei c und d Konstanten sind
Verwenden Sie daher diese Wiederholungsrelation,
$$ T (n) = 2 ^ i T (\ frac {n} {2 ^ i}) + idn $$
As, $ i = log \: n, \: T (n) = 2 ^ {log \: n} T (\ frac {n} {2 ^ {log \: n}}) + log \: ndn $
$ = \: cn + dnlog \: n $
Daher ist $ T (n) = O (n \: log \: n) $
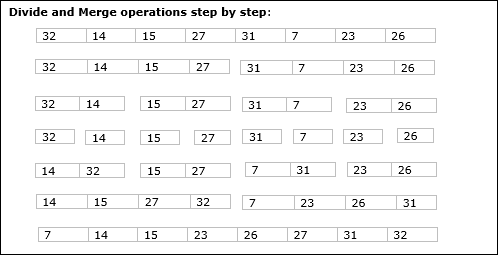
Beispiel
Im folgenden Beispiel haben wir den Merge-Sort-Algorithmus Schritt für Schritt gezeigt. Zunächst wird jedes Iterationsarray in zwei Unterarrays unterteilt, bis das Unterarray nur noch ein Element enthält. Wenn diese Unterarrays nicht weiter unterteilt werden können, werden Zusammenführungsvorgänge ausgeführt.