DAA - Mehrstufiges Diagramm

Ein mehrstufiges Diagramm G = (V, E) ist ein gerichteter Graph, in den Eckpunkte unterteilt sind k (wo k > 1) Anzahl der disjunkten Teilmengen S = {s₁,s₂,…,s_k}so dass die Kante (u, v) in E ist, dann ist u _i s _i und v Є s _{1 + 1} für einige Teilmengen in der Partition und |s₁| = |s_k| = 1.

Der Scheitelpunkt s Є s₁ heißt das source und der Scheitelpunkt t Є s_k wird genannt sink.

Gwird normalerweise als gewichteter Graph angenommen. In diesem Diagramm werden die Kosten einer Kante (i, j) durch c (i, j) dargestellt . Daher die Kosten für den Pfad von der Quelles sinken t ist die Summe der Kosten jeder Kante in diesem Pfad.

Das mehrstufige Diagrammproblem besteht darin, den Pfad mit minimalen Kosten von der Quelle zu finden s sinken t.

Beispiel

Betrachten Sie das folgende Beispiel, um das Konzept des mehrstufigen Diagramms zu verstehen.

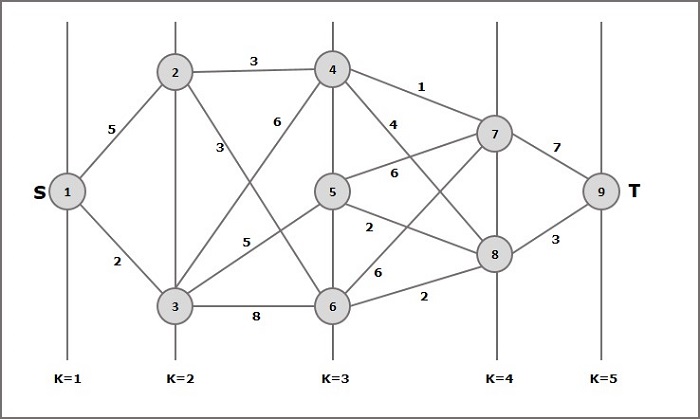
Nach der Formel müssen wir die Kosten berechnen (i, j) Verwenden Sie die folgenden Schritte

Schritt 1: Kosten (K-2, j)

In diesem Schritt werden drei Knoten (Knoten 4, 5. 6) als ausgewählt j. Daher haben wir drei Möglichkeiten, um die Mindestkosten in diesem Schritt zu wählen.

Kosten (3, 4) = min {c (4, 7) + Kosten (7, 9), c (4, 8) + Kosten (8, 9)} = 7

Kosten (3, 5) = min {c (5, 7) + Kosten (7, 9), c (5, 8) + Kosten (8, 9)} = 5

Kosten (3, 6) = min {c (6, 7) + Kosten (7, 9), c (6, 8) + Kosten (8, 9)} = 5

Schritt 2: Kosten (K-3, j)

Zwei Knoten werden als j ausgewählt, da im Stadium k - 3 = 2 zwei Knoten 2 und 3 vorhanden sind. Der Wert i = 2 und j = 2 und 3.

Kosten (2, 2) = min {c (2, 4) + Kosten (4, 8) + Kosten (8, 9), c (2, 6) +

Kosten (6, 8) + Kosten (8, 9)} = 8

Kosten (2, 3) = {c (3, 4) + Kosten (4, 8) + Kosten (8, 9), c (3, 5) + Kosten (5, 8) + Kosten (8, 9), c (3, 6) + Kosten (6, 8) + Kosten (8, 9)} = 10

Schritt 3: Kosten (K-4, j)

Kosten (1, 1) = {c (1, 2) + Kosten (2, 6) + Kosten (6, 8) + Kosten (8, 9), c (1, 3) + Kosten (3, 5) + Kosten (5, 8) + Kosten (8, 9))} = 12

c (1, 3) + Kosten (3, 6) + Kosten (6, 8 + Kosten (8, 9))} = 13

Daher ist der Weg mit den minimalen Kosten 1→ 3→ 5→ 8→ 9.