DAA - Optimales Zusammenführungsmuster
Führen Sie eine Reihe sortierter Dateien unterschiedlicher Länge zu einer einzigen sortierten Datei zusammen. Wir müssen eine optimale Lösung finden, bei der die resultierende Datei in kürzester Zeit generiert wird.
Wenn die Anzahl der sortierten Dateien angegeben ist, gibt es viele Möglichkeiten, sie zu einer einzigen sortierten Datei zusammenzuführen. Diese Zusammenführung kann paarweise durchgeführt werden. Daher wird diese Art der Zusammenführung als bezeichnet2-way merge patterns.
Da unterschiedliche Paarungen unterschiedliche Zeit benötigen, möchten wir in dieser Strategie einen optimalen Weg zum Zusammenführen vieler Dateien ermitteln. Bei jedem Schritt werden zwei kürzeste Sequenzen zusammengeführt.
Zusammenführen von a p-record file und ein q-record file erfordert möglicherweise p + q Rekordbewegungen, wobei die offensichtliche Wahl darin besteht, die beiden kleinsten Dateien bei jedem Schritt zusammenzuführen.
Zweiwege-Zusammenführungsmuster können durch binäre Zusammenführungsbäume dargestellt werden. Betrachten wir eine Reihe vonn sortierte Dateien {f1, f2, f3, …, fn}. Anfänglich wird jedes Element davon als ein einzelner Knoten-Binärbaum betrachtet. Um diese optimale Lösung zu finden, wird der folgende Algorithmus verwendet.
Algorithm: TREE (n)
for i := 1 to n – 1 do
declare new node
node.leftchild := least (list)
node.rightchild := least (list)
node.weight) := ((node.leftchild).weight) + ((node.rightchild).weight)
insert (list, node);
return least (list);Am Ende dieses Algorithmus repräsentiert das Gewicht des Wurzelknotens die optimalen Kosten.
Beispiel
Betrachten wir die gegebenen Dateien f 1 , f 2 , f 3 , f 4 und f 5 mit einer Anzahl von 20, 30, 10, 5 bzw. 30 Elementen.
Wenn Zusammenführungsvorgänge gemäß der angegebenen Reihenfolge ausgeführt werden, dann
M1 = merge f1 and f2 => 20 + 30 = 50
M2 = merge M1 and f3 => 50 + 10 = 60
M3 = merge M2 and f4 => 60 + 5 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Daher beträgt die Gesamtzahl der Operationen
50 + 60 + 65 + 95 = 270
Nun stellt sich die Frage, ob es eine bessere Lösung gibt.
Wenn wir die Zahlen nach ihrer Größe in aufsteigender Reihenfolge sortieren, erhalten wir die folgende Reihenfolge:
f4, f3, f1, f2, f5
Daher können Zusammenführungsoperationen für diese Sequenz ausgeführt werden
M1 = merge f4 and f3 => 5 + 10 = 15
M2 = merge M1 and f1 => 15 + 20 = 35
M3 = merge M2 and f2 => 35 + 30 = 65
M4 = merge M3 and f5 => 65 + 30 = 95
Daher beträgt die Gesamtzahl der Operationen
15 + 35 + 65 + 95 = 210
Offensichtlich ist dies besser als das vorherige.
In diesem Zusammenhang werden wir nun das Problem mit diesem Algorithmus lösen.
Erster Satz

Schritt 1
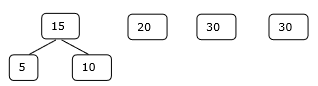
Schritt 2
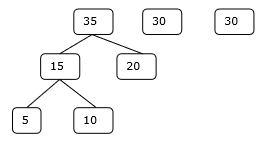
Schritt 3
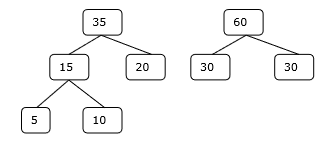
Schritt 4
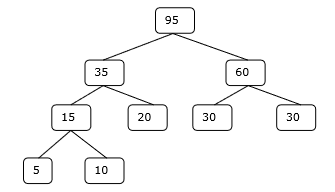
Daher benötigt die Lösung 15 + 35 + 60 + 95 = 205 Vergleiche.