DAA - Einfügemethode
Um ein Element in einen Heap einzufügen, wird das neue Element zunächst als letztes Element des Arrays an das Ende des Heaps angehängt.
Nach dem Einfügen dieses Elements kann die Heap-Eigenschaft verletzt werden. Daher wird die Heap-Eigenschaft repariert, indem das hinzugefügte Element mit seinem übergeordneten Element verglichen und das hinzugefügte Element um eine Ebene nach oben verschoben wird, wobei Positionen mit dem übergeordneten Element ausgetauscht werden. Dieser Vorgang wird aufgerufenpercolation up.
Der Vergleich wird wiederholt, bis der Elternteil größer oder gleich dem Perkolationselement ist.
Algorithm: Max-Heap-Insert (numbers[], key)
heapsize = heapsize + 1
numbers[heapsize] = -∞
i = heapsize
numbers[i] = key
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i]
exchange(numbers[i], numbers[Parent(numbers[], i)])
i = Parent (numbers[], i)Analyse
Zunächst wird am Ende des Arrays ein Element hinzugefügt. Wenn es die Heap-Eigenschaft verletzt, wird das Element mit seinem übergeordneten Element ausgetauscht. Die Höhe des Baumes istlog n. Maximallog n Anzahl der Operationen muss ausgeführt werden.
Daher ist die Komplexität dieser Funktion O(log n).
Beispiel
Betrachten wir einen Max-Heap, wie unten gezeigt, bei dem ein neues Element 5 hinzugefügt werden muss.
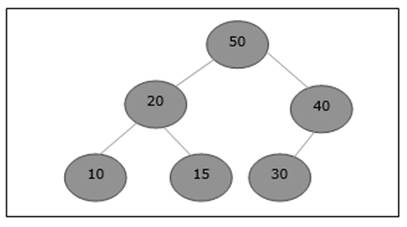
Am Ende dieses Arrays werden zunächst 55 hinzugefügt.
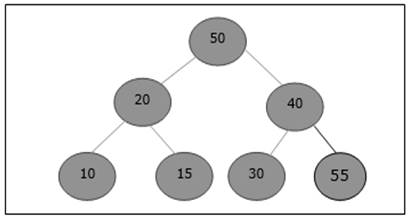
Nach dem Einfügen wird die Heap-Eigenschaft verletzt. Daher muss das Element mit seinem übergeordneten Element ausgetauscht werden. Nach dem Tausch sieht der Heap wie folgt aus.
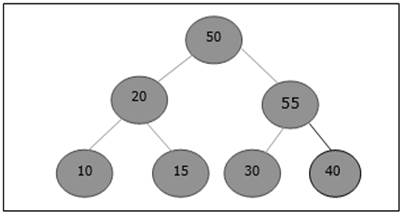
Auch hier verletzt das Element die Eigenschaft von Heap. Daher wird es mit seinem Elternteil getauscht.
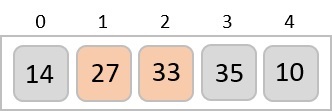
Jetzt müssen wir aufhören.