Modélisation de la division d'un nombre entier par une fraction
Ici, dans cette leçon, nous apprenons à utiliser le modèle d'aire pour diviser un nombre entier par une fraction. Il y a un nombre entier et une fraction qui divise ce nombre entier. Nous considérons un nombre entier comme autant de carrés que le nombre l'indique. Nous divisons chacun des carrés en autant de parties que le dénominateur de la fraction l'indique. On trouve le résultat de cette division en comptant le nombre total de parties des carrés.
Example:
Divisez 3 ÷ $ \ frac {1} {2} $ en utilisant un modèle d'aire.
Solution
Step 1:
Le nombre entier 3 est considéré comme trois carrés. Comme la fraction est de moitié, chacun des carrés est divisé en deux moitiés.
Step 2:
Maintenant, les moitiés des trois carrés sont comptées et se révèlent être 6. C'est la réponse que nous obtenons en divisant 3 par $ \ frac {1} {2} $ .
Donc, 3 ÷ $ \ frac {1} {2} $ = 6
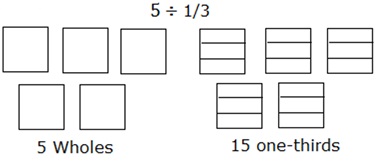
Divisez 5 ÷ $ \ frac {1} {3} $ en utilisant un modèle d'aire.
Solution
Step 1:
La division de 5 en un tiers peut être modélisée comme suit:
Considérez 5 carrés comme 5 entiers. Chacun des carrés est divisé en trois parties ou un tiers.
Step 2:
Puis compter le nombre total de telles parties des carrés ou des ensembles donne la réponse qui est 15.
Donc, 5 ÷ $ \ frac {1} {3} $ = 15
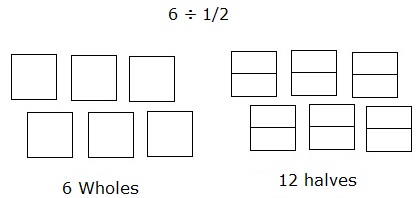
Divisez 6 ÷ $ \ frac {1} {2} $ en utilisant un modèle d'aire.
Solution
Step 1:
La division de 6 en deux moitiés peut être modélisée comme suit:
Considérez 6 carrés comme 6 entiers. Chacun des carrés est divisé en deux parties ou en une moitié.
Step 2:
Puis compter le nombre total de telles parties des carrés ou des ensembles donne la réponse qui est 12.
Donc, 6 ÷ $ \ frac {1} {2} $ = 12