एक वृत्त का आंशिक भाग
एक पूर्ण या पूरे वृत्त को 1 के रूप में लिया जाता है और मंडलियों के कुछ हिस्सों को भिन्न के रूप में दर्शाया जाता है। उदाहरण के लिए, यदि किसी वृत्त को 8 बराबर भागों में विभाजित किया जाता है, तो प्रत्येक भाग 1/8 भाग को दर्शाता है। इस तरह के चक्र के तीन भाग 3/8 और पर का प्रतिनिधित्व करेंगे।
यहां हम एक प्रकार की समस्याओं से निपट रहे हैं, जहां एक सर्कल में कुछ हिस्सों का प्रतिनिधित्व करने वाले अंश दिए गए हैं और हमें सर्कल के शेष अज्ञात हिस्से का प्रतिनिधित्व करने वाले अंश को खोजने की आवश्यकता है। ऐसी समस्याओं को हल करने के लिए, हम आंशिक भागों का प्रतिनिधित्व करने वाले अंशों को जोड़ते हैं और फिर 1, पूरे सर्कल से राशि घटाते हैं। परिणाम सर्कल के अज्ञात आंशिक भाग का प्रतिनिधित्व करने वाला अंश देता है।
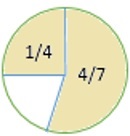
सर्कल का कितना हिस्सा अपरिवर्तित है? अपने उत्तर को सरलतम रूप में एक अंश के रूप में लिखें।
उपाय
Step 1:
पहले हम पाते हैं कि आकृति का कुल भाग क्या है।
$ \ frac {1} {4} $ + $ \ frac {4} {7} $ = $ \ frac {7} {28} $ + $ \ frac {16} {28} $ = $ \ frac {(7) +16)} {28} $ = $ \ frac {23} {28} $
Step 2:
जो आंकड़ा अपरिवर्तित है उसका अंश खोजने के लिए, हमने 1 से परिणाम प्राप्त किया ( $ \ frac {23} {28} $ )।
1 - $ \ frac {23} {28} $ = $ \ frac {28} {28} $ - $ \ frac {23} {28} $ = $ \ frac {(28−23) {28} $ = $ \ frac {5} {28} $
तो, जो आंकड़ा अपरिवर्तित है, वह $ \ frac {5} {28} $ है ।
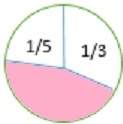
सर्कल का कितना हिस्सा छायांकित है? अपने उत्तर को सरलतम रूप में एक अंश के रूप में लिखें।
उपाय
Step 1:
पहले हम यह पता लगाते हैं कि कितना आंकड़ा अपरिवर्तित है।
$ \ frac {1} {5} $ + $ \ frac {1} {3} $ = $ \ frac {3} {15} $ + $ \ frac {5} {15} $ = $ \ frac {(3) +5)} {15} $ = $ \ frac {8} {15} $
Step 2:
जो आंकड़ा अपरिवर्तित है उसका अंश खोजने के लिए हम 1 से प्राप्त परिणाम ( $ \ frac {8} {15} $ ) घटाते हैं ।
1 - $ \ frac {8} {15} $ = $ \ frac {15} {15} $ - $ \ frac {8} {15} $ = $ \ frac {(15−8)} {15} $ = $ \ frac {7} {15} $
तो, जो आंकड़ा छायांकित है, वह $ \ frac {7} {15} $ है ।