नियंत्रण प्रणाली - ब्लॉक आरेख
ब्लॉक आरेखों में एक ब्लॉक या ब्लॉक का संयोजन होता है। इनका उपयोग चित्रात्मक रूप में नियंत्रण प्रणालियों का प्रतिनिधित्व करने के लिए किया जाता है।
ब्लॉक आरेख के मूल तत्व
ब्लॉक आरेख के मूल तत्व एक ब्लॉक, योग बिंदु और टेक-ऑफ बिंदु हैं। आइए इन तत्वों की पहचान करने के लिए एक बंद लूप नियंत्रण प्रणाली के ब्लॉक आरेख पर विचार करें जो निम्न आकृति में दिखाया गया है।

उपरोक्त ब्लॉक आरेख में दो कार्य शामिल हैं जिनमें स्थानांतरण कार्य G (s) और H (s) हैं। इसमें एक योग बिंदु और एक टेक-ऑफ बिंदु भी है। तीर संकेतों के प्रवाह की दिशा का संकेत देते हैं। आइए अब हम एक-एक करके इन तत्वों पर चर्चा करते हैं।
खंड मैथा
एक घटक का स्थानांतरण कार्य एक ब्लॉक द्वारा दर्शाया गया है। ब्लॉक में एकल इनपुट और एकल आउटपुट है।
निम्नलिखित आंकड़ा इनपुट X (s), आउटपुट Y (s) और हस्तांतरण फ़ंक्शन G (s) वाले ब्लॉक को दिखाता है।

स्थानांतरण फ़ंक्शन, $ G (s) = \ frac {Y (s)} {X (s)} $
$$ \ Rightarrow Y (s) = G (s) X (s) $ $
ब्लॉक का आउटपुट इनपुट के साथ ब्लॉक के ट्रांसफर फ़ंक्शन को गुणा करके प्राप्त किया जाता है।
सूमिंग पॉइंट
योग बिंदु को इसके अंदर क्रॉस (X) वाले वृत्त के साथ दर्शाया गया है। इसमें दो या अधिक इनपुट और एकल आउटपुट हैं। यह आदानों के बीजीय योग का उत्पादन करता है। यह इनपुट की ध्रुवता के आधार पर इनपुट के योग और घटाव या संयोजन को जोड़ या घटाता भी है। आइए एक-एक करके इन तीन ऑपरेशनों को देखें।
निम्नलिखित आंकड़ा दो बिंदुओं (ए, बी) और एक आउटपुट (वाई) के साथ योग बिंदु को दर्शाता है। यहां, ए और बी इनपुट सकारात्मक संकेत है। तो, योग बिंदु आउटपुट का उत्पादन करता है, वाई के रूप मेंsum of A and B.
यानी, वाई = ए + बी।

निम्नलिखित आंकड़ा दो बिंदुओं (ए, बी) और एक आउटपुट (वाई) के साथ योग बिंदु को दर्शाता है। यहां, ए और बी के इनपुट विपरीत संकेत दे रहे हैं, यानी ए सकारात्मक संकेत दे रहा है और बी नकारात्मक संकेत दे रहा है। तो, योग बिंदु आउटपुट का उत्पादन करता हैY के रूप में difference of A and B।
वाई = ए + (-बी) = ए - बी।

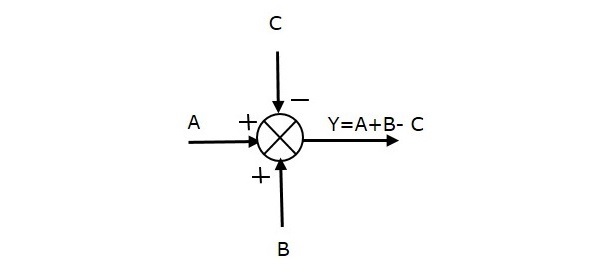
निम्नलिखित आंकड़ा तीन इनपुट (ए, बी, सी) और एक आउटपुट (वाई) के साथ योग बिंदु को दर्शाता है। यहां, ए और बी के इनपुट्स सकारात्मक संकेत दे रहे हैं और सी नकारात्मक संकेत दे रहे हैं। तो, योग बिंदु आउटपुट का उत्पादन करता हैY जैसा
Y = A + B + (−C) = A + B - C
टेक-ऑफ पॉइंट
टेक-ऑफ पॉइंट वह बिंदु है जहां से एक ही इनपुट सिग्नल को एक से अधिक ब्रांच से गुजारा जा सकता है। इसका मतलब है कि टेक-ऑफ पॉइंट की मदद से, हम एक या अधिक ब्लॉक में एक ही इनपुट लगा सकते हैं, पॉइंट्स को समेट सकते हैं।
निम्नलिखित आंकड़े में, टेक-ऑफ बिंदु का उपयोग एक ही इनपुट, आर (एस) को दो और ब्लॉकों से जोड़ने के लिए किया जाता है।

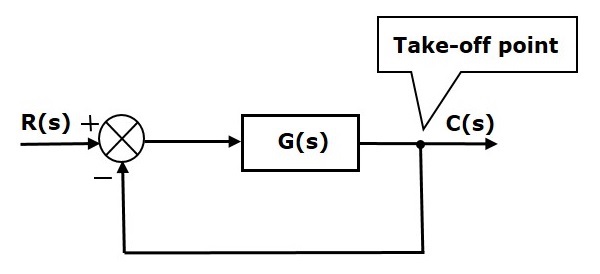
निम्न आकृति में, आउटपुट सी (एस) को जोड़ने के लिए टेक-ऑफ बिंदु का उपयोग किया जाता है, जो कि समन बिंदु के इनपुट के रूप में होता है।
विद्युत प्रणालियों के ब्लॉक आरेख प्रतिनिधित्व
इस खंड में, हम एक ब्लॉक आरेख के साथ एक विद्युत प्रणाली का प्रतिनिधित्व करते हैं। विद्युत प्रणालियों में मुख्य रूप से तीन मूल तत्व होते हैं -resistor, inductor and capacitor।
निम्नलिखित आंकड़े में दिखाए गए अनुसार RLC सर्किट की एक श्रृंखला पर विचार करें। जहाँ, V i (t) और V o (t) इनपुट और आउटपुट वोल्टेज हैं। मैं (t) सर्किट से होकर गुजरने वाली धारा हूं। यह सर्किट टाइम डोमेन में है।

इस सर्किट में लाप्लास ट्रांसफ़ॉर्म को लागू करने से, एस-डोमेन में सर्किट मिलेगा। सर्किट निम्न आकृति में दिखाया गया है।
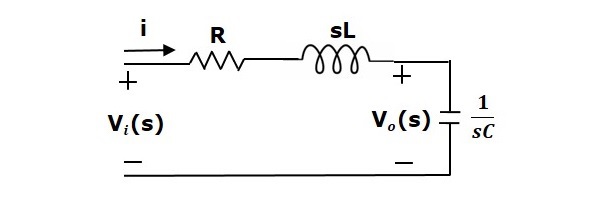
उपरोक्त सर्किट से, हम लिख सकते हैं
$$ मैं (रों) = \ frac {V_i (रों) -V_o (रों)} {आर + SL} $$
$ \ Rightarrow I (s) = \ left \ {frac {1} {R + sL} \ right \} \ left \ {V_i (s) -V_o (s) \ right \} $ (Equation 1)
$ V_o (s) = \ left (\ frac {1} {sC} \ right) I (s) $ (Equation 2)
आइए अब हम इन दो समीकरणों के लिए व्यक्तिगत रूप से ब्लॉक आरेखों को आकर्षित करते हैं। और फिर आरएलसी सर्किट (एस-डोमेन) की श्रृंखला के समग्र ब्लॉक आरेख प्राप्त करने के लिए उन ब्लॉक आरेखों को ठीक से संयोजित करें।
समीकरण 1 को हस्तांतरण फ़ंक्शन, $ \ frac {1} {R + sL} $ वाले ब्लॉक के साथ लागू किया जा सकता है। इस ब्लॉक का इनपुट और आउटपुट $ \ left \ {V_i (s) -V_o (s) \ right \} $ और $ I (s) $ है। हमें $ \ left \ {V_i (s) -V_o (s) \ right \} $ प्राप्त करने के लिए एक योग बिंदु की आवश्यकता है। समीकरण 1 का ब्लॉक आरेख निम्नलिखित आकृति में दिखाया गया है।

समीकरण 2 को हस्तांतरण समारोह, $ \ frac {1} {sC} $ वाले ब्लॉक के साथ लागू किया जा सकता है। इस ब्लॉक का इनपुट और आउटपुट $ I (s) $ और $ V_o (s) $ हैं। समीकरण 2 का ब्लॉक आरेख निम्नलिखित आकृति में दिखाया गया है।

आरएलसी सर्किट (एस-डोमेन) की श्रृंखला का समग्र ब्लॉक आरेख निम्न आकृति में दिखाया गया है।

इसी तरह, आप आकर्षित कर सकते हैं block diagram इस सरल प्रक्रिया का पालन करके किसी भी विद्युत परिपथ या प्रणाली की।
लाप्लास परिवर्तन लागू करके समय डोमेन विद्युत सर्किट को एस-डोमेन विद्युत सर्किट में परिवर्तित करें।
सभी शंट शाखाओं में सभी श्रृंखला शाखा तत्वों और वोल्टेज से गुजरने वाले वर्तमान के लिए समीकरणों को लिखें।
उपरोक्त सभी समीकरणों के लिए व्यक्तिगत रूप से ब्लॉक आरेख खींचें।
इलेक्ट्रिकल सर्किट (एस-डोमेन) के समग्र ब्लॉक आरेख को प्राप्त करने के लिए इन सभी ब्लॉक आरेखों को ठीक से मिलाएं।