नियंत्रण प्रणाली - समय प्रतिक्रिया विश्लेषण
हम समय डोमेन और आवृत्ति डोमेन दोनों में नियंत्रण प्रणालियों की प्रतिक्रिया का विश्लेषण कर सकते हैं। हम बाद के अध्यायों में नियंत्रण प्रणालियों की आवृत्ति प्रतिक्रिया विश्लेषण पर चर्चा करेंगे। आइए अब नियंत्रण प्रणालियों के समय प्रतिक्रिया विश्लेषण के बारे में चर्चा करते हैं।
समय प्रतिक्रिया क्या है?
यदि इनपुट के लिए नियंत्रण प्रणाली का आउटपुट समय के साथ बदलता रहता है, तो इसे कहा जाता है time responseनियंत्रण प्रणाली का। समय प्रतिक्रिया में दो भाग होते हैं।
- अस्थायी प्रतिसाद
- स्थिर राज्य प्रतिक्रिया
समय क्षेत्र में नियंत्रण प्रणाली की प्रतिक्रिया निम्न आकृति में दिखाई गई है।

यहाँ, दोनों क्षणिक और स्थिर अवस्थाओं को चित्र में दर्शाया गया है। इन राज्यों के अनुरूप प्रतिक्रियाओं को क्षणिक और स्थिर राज्य प्रतिक्रियाओं के रूप में जाना जाता है।
गणितीय रूप से, हम समय प्रतिक्रिया c (t) के रूप में लिख सकते हैं
$$ ग (टी) = c_ {टीआर} (टी) + c_ {एस एस} (टी) $$
कहाँ पे,
- c tr (t) क्षणिक प्रतिक्रिया है
- c ss (t) स्थिर अवस्था प्रतिक्रिया है
अस्थायी प्रतिसाद
नियंत्रण प्रणाली में इनपुट लागू करने के बाद, आउटपुट को स्थिर स्थिति तक पहुंचने में निश्चित समय लगता है। इसलिए, उत्पादन क्षणिक स्थिति में होगा जब तक कि यह स्थिर स्थिति में नहीं जाता है। इसलिए, क्षणिक स्थिति के दौरान नियंत्रण प्रणाली की प्रतिक्रिया के रूप में जाना जाता हैtransient response।
क्षणिक प्रतिक्रिया 'टी' के बड़े मूल्यों के लिए शून्य होगी। आदर्श रूप से, 't' का यह मान अनंत है और व्यावहारिक रूप से, यह पाँच गुना स्थिर है।
गणितीय रूप से, हम इसे लिख सकते हैं
$ $ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $ $
स्थिर राज्य प्रतिक्रिया
क्षणिक प्रतिक्रिया के बाद भी बने रहने वाले समय की प्रतिक्रिया के हिस्से को 't' के बड़े मूल्यों के लिए शून्य मान के रूप में जाना जाता है steady state response। इसका मतलब है, स्थिर अवस्था के दौरान भी क्षणिक प्रतिक्रिया शून्य होगी।
Example
आइए हम नियंत्रण प्रणाली $ c (t) = 10 + 5e ^ {{- t} $ की समय प्रतिक्रिया की क्षणिक और स्थिर स्थिति को खोजें।
यहां, दूसरा शब्द $ 5e ^ {- t} $ के रूप में शून्य होगा tअनन्तता को दर्शाता है। तो, यह हैtransient term। और पहला शब्द 10 भी बना हुआ हैtअनंत तक पहुंचता है। तो, यह हैsteady state term।
मानक परीक्षण संकेत
मानक परीक्षण संकेत आवेग, कदम, रैंप और पैराबोलिक हैं। इन संकेतों का उपयोग आउटपुट के समय की प्रतिक्रिया का उपयोग करके नियंत्रण प्रणालियों के प्रदर्शन को जानने के लिए किया जाता है।
यूनिट आवेग संकेत
एक इकाई आवेग संकेत, δ (टी) के रूप में परिभाषित किया गया है
$ \ डेल्टा (t) = $ $ के लिए $ t \ neq ० $
और $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
निम्नलिखित आंकड़ा इकाई आवेग संकेत दिखाता है।

तो, इकाई आवेग संकेत केवल 'टी' पर मौजूद है जो शून्य के बराबर है। 'टी' के चारों ओर छोटे अंतराल के तहत इस सिग्नल का क्षेत्र शून्य के बराबर है। यूनिट आवेग संकेत का मान 't' के अन्य सभी मानों के लिए शून्य है।
यूनिट स्टेप सिग्नल
एक इकाई चरण संकेत, यू (टी) के रूप में परिभाषित किया गया है
$$ u (t) = 1; t \ geq 0 $ $
$ = 0; टी <0 $
निम्नलिखित आंकड़ा इकाई चरण संकेत दिखाता है।

तो, शून्य सहित 'टी' के सभी सकारात्मक मूल्यों के लिए इकाई चरण संकेत मौजूद है। और इस अंतराल के दौरान इसका मूल्य एक है। 'T' के सभी नकारात्मक मानों के लिए इकाई चरण संकेत का मान शून्य है।
यूनिट रैंप सिग्नल
एक इकाई रैंप सिग्नल, आर (टी) के रूप में परिभाषित किया गया है
$$ आर (टी) = टी; t \ geq 0 $ $
$ = 0; टी <0 $
हम यूनिट रैंप सिग्नल, $ r (t) $ को यूनिट स्टेप सिग्नल, $ u (t) $ के रूप में लिख सकते हैं
$$ आर (टी) = तू (टी) $$
निम्नलिखित आंकड़ा इकाई रैंप संकेत दिखाता है।

तो, यूनिट रैंप सिग्नल शून्य सहित 'टी' के सभी सकारात्मक मूल्यों के लिए मौजूद है। और इस अंतराल के दौरान 'टी' के संबंध में इसका मूल्य रैखिक रूप से बढ़ जाता है। 'टी' के सभी नकारात्मक मूल्यों के लिए यूनिट रैंप सिग्नल का मूल्य शून्य है।
यूनिट परवलयिक संकेत
एक इकाई परवलयिक संकेत, पी (टी) के रूप में परिभाषित किया गया है,
$$ पी (टी) = \ frac {टी ^ 2} {2}; t \ geq 0 $ $
$ = 0; टी <0 $
हम इकाई चरण संकेत, $ p (t) $ को इकाई चरण संकेत, $ u (t) $ के रूप में लिख सकते हैं,
$$ पी (टी) = \ frac {टी ^ 2} {2} यू (टी) $$
निम्नलिखित आंकड़ा इकाई परवलयिक संकेत दिखाता है।
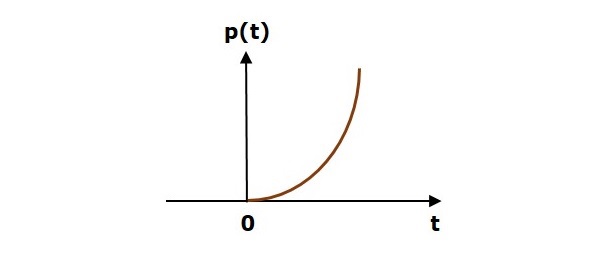
तो, इकाई परवलयिक संकेत सभी के सकारात्मक मूल्यों के लिए मौजूद है ‘t’शून्य सहित। और इस अंतराल के दौरान 'टी' के संबंध में इसका मूल्य गैर-रैखिक रूप से बढ़ जाता है। 'T' के सभी नकारात्मक मानों के लिए इकाई परवलयिक संकेत का मान शून्य है।