मैकेनिकल सिस्टम की विद्युत एनालॉग्स
दो प्रणालियों के लिए कहा जाता है analogous एक दूसरे को अगर निम्न दो स्थितियां संतुष्ट हैं।
- दोनों प्रणालियाँ शारीरिक रूप से भिन्न हैं
- इन दोनों प्रणालियों के विभेदक समीकरण मॉडलिंग समान हैं
इलेक्ट्रिकल सिस्टम और मैकेनिकल सिस्टम दो शारीरिक रूप से अलग सिस्टम हैं। ट्रांसलेशनल मैकेनिकल सिस्टम की दो प्रकार की विद्युत उपमाएँ हैं। वे बल वोल्टेज सादृश्य हैं और वर्तमान सादृश्य को बल देते हैं।
बल वोल्टेज सादृश्य
बल वोल्टेज सादृश्य में, के गणितीय समीकरण translational mechanical system विद्युत प्रणाली के मेष समीकरणों के साथ तुलना की जाती है।
निम्नलिखित आंकड़ा यांत्रिक प्रणाली पर विचार करें जैसा कि निम्नलिखित आकृति में दिखाया गया है।
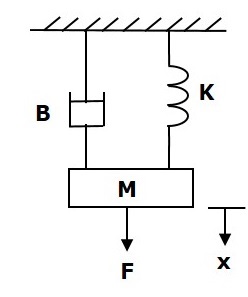
force balanced equation इस प्रणाली के लिए है
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (Equation 1)
निम्न विद्युत प्रणाली पर विचार करें जैसा कि निम्नलिखित आकृति में दिखाया गया है। इस सर्किट में एक रोकनेवाला, एक प्रारंभ करनेवाला और एक संधारित्र होता है। ये सभी विद्युत तत्व एक श्रृंखला में जुड़े हुए हैं। इस सर्किट पर लागू इनपुट वोल्टेज है$V$ सर्किट के माध्यम से वोल्ट और करंट प्रवाहित होता है $i$ Amps।

इस सर्किट के लिए मेष समीकरण है
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (Equation 2)
विकल्प, $i=\frac{\text{d}q}{\text{d}t}$ समीकरण 2 में।
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (Equation 3)
समीकरण 1 और समीकरण 3 की तुलना करने से, हमें अनुवादकीय यांत्रिक प्रणाली और विद्युत प्रणाली के अनुरूप मात्रा मिलेगी। निम्न तालिका इन अनुरूप मात्राओं को दिखाती है।
| ट्रांसलेशनल मैकेनिकल सिस्टम | विद्युत प्रणाली |
|---|---|
| बल (एफ) | वोल्टेज (V) |
| जन (एम) | उपपादन (एल) |
| घर्षण गुणांक (B) | प्रतिरोध (आर) |
| स्प्रिंग कॉन्सटेंट (K) | कैपेसिटेंस का पारस्परिक $(\frac{1}{c})$ |
| विस्थापन (एक्स) | प्रभारी (क्यू) |
| वेग (v) | वर्तमान (i) |
इसी तरह, घूर्णी यांत्रिक प्रणालियों के लिए टोक़ वोल्टेज सादृश्य है। आइए अब इस सादृश्य के बारे में चर्चा करते हैं।
टोक़ वोल्टेज सादृश्य
इस सादृश्य में, गणितीय समीकरणों का rotational mechanical system विद्युत प्रणाली के मेष समीकरणों के साथ तुलना की जाती है।
घूर्णी यांत्रिक प्रणाली को निम्न आकृति में दिखाया गया है।

टॉर्क संतुलित समीकरण है
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t}+k\theta$ (Equation 4)
समीकरण 4 और समीकरण 3 की तुलना करके, हम घूर्णी यांत्रिक प्रणाली और विद्युत प्रणाली के अनुरूप मात्रा प्राप्त करेंगे। निम्न तालिका इन अनुरूप मात्राओं को दिखाती है।
| घूर्णी यांत्रिक प्रणाली | विद्युत प्रणाली |
|---|---|
| टॉर्क (टी) | वोल्टेज (V) |
| पल की जड़ता (जे) | उपपादन (एल) |
| घूर्णी घर्षण गुणांक (B) | प्रतिरोध (आर) |
| आंशिक वसंत स्थिरांक (K) | कैपेसिटेंस का पारस्परिक $(\frac{1}{c})$ |
| कोणीय विस्थापन (() | प्रभारी (क्यू) |
| कोणीय वेग (ω) | वर्तमान (i) |
बल वर्तमान सादृश्य
वर्तमान सादृश्य में, के गणितीय समीकरण translational mechanical system विद्युत प्रणाली के नोडल समीकरणों के साथ तुलना की जाती है।
निम्न विद्युत प्रणाली पर विचार करें जैसा कि निम्नलिखित आकृति में दिखाया गया है। इस सर्किट में वर्तमान स्रोत, रोकनेवाला, प्रारंभ करनेवाला और संधारित्र होते हैं। ये सभी विद्युत तत्व समानांतर में जुड़े हुए हैं।

नोडल समीकरण है
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$ (Equation 5)
विकल्प, $V=\frac{\text{d}\Psi}{\text{d}t}$ समीकरण 5 में।
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C\frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (Equation 6)
समीकरण 1 और समीकरण 6 की तुलना करने से, हमें अनुवादकीय यांत्रिक प्रणाली और विद्युत प्रणाली के अनुरूप मात्रा मिलेगी। निम्न तालिका इन अनुरूप मात्राओं को दिखाती है।
| ट्रांसलेशनल मैकेनिकल सिस्टम | विद्युत प्रणाली |
|---|---|
| बल (एफ) | वर्तमान (i) |
| जन (एम) | समाई (सी) |
| घर्षण गुणांक (B) | प्रतिरोध का पारस्परिक$(\frac{1}{R})$ |
| वसंत स्थिरांक (K) | अनिर्णय का प्रतिक्षेप$(\frac{1}{L})$ |
| विस्थापन (एक्स) | चुंबकीय प्रवाह (ψ) |
| वेग (v) | वोल्टेज (V) |
इसी तरह, घूर्णी यांत्रिक प्रणालियों के लिए एक टोक़ वर्तमान सादृश्य है। आइए अब इस सादृश्य पर चर्चा करते हैं।
टोक़ वर्तमान सादृश्य
इस सादृश्य में, गणितीय समीकरणों की rotational mechanical system विद्युत प्रणाली के नोडल मेष समीकरणों के साथ तुलना की जाती है।
समीकरण 4 और समीकरण 6 की तुलना करके, हम घूर्णी यांत्रिक प्रणाली और विद्युत प्रणाली के अनुरूप मात्रा प्राप्त करेंगे। निम्न तालिका इन अनुरूप मात्राओं को दिखाती है।
| घूर्णी यांत्रिक प्रणाली | विद्युत प्रणाली |
|---|---|
| टॉर्क (टी) | वर्तमान (i) |
| जड़ता का क्षण (जे) | समाई (सी) |
| घूर्णी घर्षण गुणांक (B) | प्रतिरोध का पारस्परिक$(\frac{1}{R})$ |
| आंशिक वसंत स्थिरांक (K) | अनिर्णय का प्रतिक्षेप$(\frac{1}{L})$ |
| कोणीय विस्थापन (() | चुंबकीय प्रवाह (ψ) |
| कोणीय वेग (ω) | वोल्टेज (V) |
इस अध्याय में, हमने यांत्रिक प्रणालियों की विद्युत उपमाओं पर चर्चा की। ये उपमाएँ गैर-विद्युत प्रणाली का अध्ययन और विश्लेषण करने में सहायक होती हैं, जैसे कि यांत्रिक विद्युत प्रणाली से यांत्रिक प्रणाली।