मैकेनिकल सिस्टम की मॉडलिंग
इस अध्याय में, आइए चर्चा करते हैं differential equation modelingमैकेनिकल सिस्टम की। गति के प्रकार के आधार पर दो प्रकार की यांत्रिक प्रणालियाँ हैं।
- ट्रांसलेशनल मैकेनिकल सिस्टम
- घूर्णी यांत्रिक प्रणाली
ट्रांसलेशनल मैकेनिकल सिस्टम्स की मॉडलिंग
ट्रांसलैशनल मैकेनिकल सिस्टम साथ चलते हैं straight line। इन प्रणालियों में मुख्य रूप से तीन मूल तत्व होते हैं। वे बड़े पैमाने पर हैं, वसंत और पानी का छींटा या स्पंज।
यदि एक बल को एक यांत्रिक यांत्रिक प्रणाली के लिए लागू किया जाता है, तो इसका द्रव्यमान, लोच और प्रणाली के घर्षण के कारण विरोधी शक्तियों द्वारा विरोध किया जाता है। चूंकि लागू बल और विरोधी बल विपरीत दिशाओं में हैं, सिस्टम पर काम करने वाले बलों का बीजगणितीय योग शून्य है। आइए अब हम इन तीन तत्वों द्वारा व्यक्तिगत रूप से विरोध किया गया बल देखें।
द्रव्यमान
द्रव्यमान एक पिंड का गुण है, जो भंडार करता है kinetic energy। यदि एक बल द्रव्यमान वाले शरीर पर लागू किया जाता हैM, तो यह द्रव्यमान के कारण एक विरोधी बल द्वारा विरोध किया जाता है। यह विरोधी बल शरीर के त्वरण के समानुपाती होता है। मान लो लोच और घर्षण नगण्य हैं।

$ $ F_m \ propto \: एक $ $
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $ $
$$ एफ = F_m = एम \ frac {\ text {घ} ^ 2x} {\ text {घ} टी ^ 2} $$
कहाँ पे,
F लागू बल है
Fm द्रव्यमान के कारण विरोधी बल है
M द्रव्यमान है
a त्वरण है
x विस्थापन है
वसंत
वसंत एक तत्व है, जो संग्रहीत करता है potential energy। यदि एक बल वसंत पर लगाया जाता हैK, तो यह वसंत की लोच के कारण एक विरोधी बल द्वारा विरोध किया जाता है। यह विरोधी बल वसंत के विस्थापन के समानुपाती होता है। मान लें कि द्रव्यमान और घर्षण नगण्य हैं।

$ $ F \ propto \: x $ $
$$ \ Rightarrow F_k = Kx $ $
$$ एफ = F_k = Kx $$
कहाँ पे,
F लागू बल है
Fk वसंत की लोच के कारण विरोधी बल है
K वसंत स्थिर है
x विस्थापन है
Dashpot
यदि डैशपॉट पर बल लगाया जाता है B, तब इसका विरोध विरोधी बल द्वारा किया जाता है frictionपानी का छींटा। यह विरोधी बल शरीर के वेग के समानुपाती होता है। मान लें कि द्रव्यमान और लोच नगण्य हैं।

$ $ F_b \ propto \: \ n $ $
$$ \ Rightarrow F_b = B \ n = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ एफ = F_b = बी \ frac {\ text {घ} x} {\ text {घ} टी} $$
कहाँ पे,
Fb पानी का छींटा घर्षण के कारण विरोधी बल है
B घर्षण गुणांक है
v वेग है
x विस्थापन है
घूर्णी यांत्रिक प्रणालियों की मॉडलिंग
घूर्णी यांत्रिक प्रणालियां एक निश्चित अक्ष के बारे में चलती हैं। इन प्रणालियों में मुख्य रूप से तीन मूल तत्व होते हैं। वो हैmoment of inertia, torsional spring तथा dashpot।
यदि एक टोक़ को घूर्णी यांत्रिक प्रणाली पर लागू किया जाता है, तो यह प्रणाली की जड़ता, लोच और घर्षण के क्षण के कारण टोरों का विरोध करके विरोध किया जाता है। चूंकि लागू टॉर्क और विरोधी टॉरेज विपरीत दिशाओं में हैं, सिस्टम पर कार्य करने वाले टॉर्क का बीजगणितीय योग शून्य है। आइए अब हम इन तीन तत्वों द्वारा व्यक्तिगत रूप से विरोध किए गए टोक़ को देखते हैं।
निष्क्रियता के पल
ट्रांसलेशनल मैकेनिकल सिस्टम में, द्रव्यमान गतिज ऊर्जा को संग्रहीत करता है। इसी तरह, घूर्णी यांत्रिक प्रणाली में, जड़ता के भंडार का क्षणkinetic energy।
यदि जड़ता के क्षण वाले शरीर पर एक टोक़ लगाया जाता है J, तो यह जड़ता के क्षण के कारण एक विरोधी टोक द्वारा विरोध किया जाता है। यह विरोधी टोक़ शरीर के कोणीय त्वरण के लिए आनुपातिक है। मान लो लोच और घर्षण नगण्य हैं।

$ $ T_j \ propto \: \ Alpha $ $
$$ \ Rightarrow T_j = J \ Alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $ $
$$ टी = T_j = जम्मू \ frac {\ text {घ} ^ 2 \ थीटा} {\ text {घ} टी ^ 2} $$
कहाँ पे,
T लागू टॉर्क है
Tj जड़ता के क्षण के कारण विरोधी टोक़ है
J जड़ता का क्षण है
α कोणीय त्वरण है
θ कोणीय विस्थापन है
मरोड़ वसंत
ट्रांसलेशनल मैकेनिकल सिस्टम में, स्प्रिंग संभावित ऊर्जा का भंडारण करता है। इसी तरह, घूर्णी यांत्रिक प्रणाली में, मरोड़ वाले वसंत भंडारpotential energy।
यदि मरोड़ वसंत पर एक टोक़ लगाया जाता है K, तब इसका विरोध टॉर्सनल स्प्रिंग की लोच के कारण एक विरोधी टोक़ द्वारा किया जाता है। यह विरोध करने वाला टोक़ मरोड़ वाले वसंत के कोणीय विस्थापन के समानुपाती होता है। यह मान लें कि जड़ता और घर्षण के क्षण नगण्य हैं।
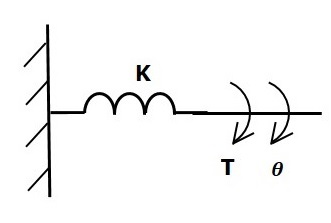
$ $ T_k \ propto \: \ थीटा $$
$$ \ Rightarrow T_k = K \ theta $$
$$ टी = T_k = कश्मीर \ थीटा $$
कहाँ पे,
T लागू टॉर्क है
Tk टॉर्सनल स्प्रिंग की लोच के कारण विरोधी टोक़ है
K मरोड़ वसंत है
θ कोणीय विस्थापन है
Dashpot
यदि डैशपॉट पर टॉर्क लगाया जाता है B, तब इसका विरोध एक विरोधी टॉर्क के कारण होता है rotational frictionपानी का छींटा। यह विरोधी टोक़ शरीर के कोणीय वेग के समानुपाती होता है। जड़ता और लोच के क्षण को नगण्य मान लें।
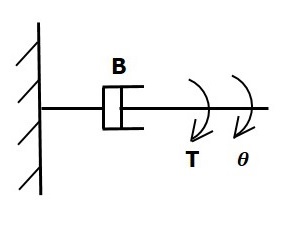
$ $ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ टी = T_b = बी \ frac {\ text {घ} \ थीटा} {\ text {घ} टी} $$
कहाँ पे,
Tb डैशपॉट के घूर्णी घर्षण के कारण विरोधी टोक़ है
B घूर्णी घर्षण गुणांक है
ω कोणीय वेग है
θ कोणीय विस्थापन है