प्रथम आदेश प्रणाली की प्रतिक्रिया
इस अध्याय में, हम पहले आदेश प्रणाली की समय प्रतिक्रिया पर चर्चा करते हैं। बंद लूप नियंत्रण प्रणाली के निम्नलिखित ब्लॉक आरेख पर विचार करें। यहां, एक ओपन लूप ट्रांसफर फ़ंक्शन, $ \ frac {1} {sT} $ एक एकता नकारात्मक प्रतिक्रिया के साथ जुड़ा हुआ है।

हम जानते हैं कि बंद लूप नियंत्रण प्रणाली के हस्तांतरण समारोह में एकता नकारात्मक प्रतिक्रिया है,
$$ \ frac {सी (रों)} {आर (s)} = \ frac {जी (रों)} {1 + G (s)} $$
उपर्युक्त समीकरण में सब्स्टिट्यूट, $ G (s) = \ frac {1} {sT} $।
$$ \ frac {सी (रों)} {आर (s)} = \ frac {\ frac {1} {जनजाति}} {1 + \ frac {1} {जनजाति}} = \ frac {1} {जनजाति + 1} $$
S की शक्ति हर शब्द में एक है। इसलिए, उपरोक्त स्थानांतरण फ़ंक्शन पहले क्रम का है और सिस्टम को कहा जाता हैfirst order system।
हम उपरोक्त समीकरण को फिर से लिख सकते हैं
$ $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $ $
कहाँ पे,
C(s) आउटपुट सिग्नल c (t) का लाप्लास रूपांतरण है,
R(s) इनपुट सिग्नल आर (टी) का लैप्लस रूपांतरण है, और
T समय स्थिर है
टाइम डोमेन में पहले ऑर्डर सिस्टम की प्रतिक्रिया (आउटपुट) प्राप्त करने के लिए इन चरणों का पालन करें।
इनपुट सिग्नल $ r (t) $ के लाप्लास रूपांतरण को लें।
समीकरण पर विचार करें, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
उपर्युक्त समीकरण में $ R (s) $ का मूल्य।
यदि आवश्यक हो तो $ C (s) $ के आंशिक अंश करें।
व्युत्क्रम लाप्लास को $ C (s) $ में लागू करें।
पिछले अध्याय में, हमने आवेग, चरण, रैंप और पैराबोलिक जैसे मानक परीक्षण संकेतों को देखा है। आइए अब हम एक-एक करके प्रत्येक इनपुट के लिए पहले ऑर्डर सिस्टम की प्रतिक्रियाओं का पता लगाते हैं। इनपुट सिग्नल के नाम के अनुसार प्रतिक्रिया का नाम दिया गया है। उदाहरण के लिए, आवेग इनपुट के लिए प्रणाली की प्रतिक्रिया को आवेग प्रतिक्रिया कहा जाता है।
आवेग प्रतिक्रिया पहली व्यवस्था प्रणाली की
इसपर विचार करें unit impulse signal पहले ऑर्डर सिस्टम के इनपुट के रूप में।
तो, $ r (t) = \ delta (t) $
दोनों तरफ लैपलैस ट्रांसफॉर्म लागू करें।
$ आर (रों) = 1 $
समीकरण पर विचार करें, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
उपर्युक्त समीकरण में स्थानापन्न, $ R (s) = 1 $।
$ $ C (s) = \ left (\ frac {1} {sT + 1} \ right) (1) = \ frac {1} {sT + 1} $ $
लैप्लस रूपांतरों के मानक रूपों में से एक में उपरोक्त समीकरण को पुनर्व्यवस्थित करें।
$ $ C (s) = \ frac {1} {T \ left (\ s + \ frac {1} {T} \ right)} \ Rightarrow C (s) = \ frac {1} {T} \ left (\) frac {1} {s + \ _ frac {1} {T}} \ right) $$
व्युत्क्रम लाप्लास परिवर्तन को दोनों तरफ लागू करें।
$ $ c (t) = \ frac {1} {T} e ^ बाएँ ({- \ frac {t} {T}} \ right) u (t) $$
इकाई आवेग प्रतिक्रिया निम्नलिखित आकृति में दिखाई गई है।
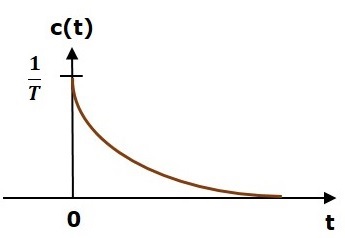
unit impulse response, c (t) 't' के सकारात्मक मूल्यों के लिए एक घातीय क्षय संकेत है और यह 't' के नकारात्मक मूल्यों के लिए शून्य है।
पहले आदेश प्रणाली के चरण प्रतिक्रिया
इसपर विचार करें unit step signal पहली व्यवस्था के लिए एक इनपुट के रूप में।
तो, $ आर (टी) = यू (टी) $
दोनों तरफ लैपलैस ट्रांसफॉर्म लागू करें।
$$ आर (रों) = \ frac {1} {s} $$
समीकरण पर विचार करें, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
उपर्युक्त समीकरण में स्थानापन्न, $ R (s) = \ frac {1} {s} $।
$ $ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s} \ right) = \ frac {1} {s \ left (sT +) 1 \ सही)} $ $
C (s) के आंशिक अंश करें।
$ $ C (s) = \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A} {s} + \ frac {B} {sT + 1} $ $
$$ \ Rightarrow \ frac {1} {s \ left (sT + 1 \ right)} = \ frac {A \ left (sT + 1 \ right) + Bs} {s \ left (sT + 1 \ right)} $$
दोनों तरफ, हर शब्द समान है। इसलिए, वे एक-दूसरे द्वारा रद्द कर दिए जाएंगे। इसलिए, अंश की शर्तों को समान करें।
$ $ 1 = A \ बाएँ (sT + 1 \ दाएँ) + B $ $ +
दोनों तरफ के स्थिर शब्दों को बराबर करके, आपको A = 1 मिलेगा।
स्थानापन्न, ए = 1 और गुणांक के बराबर है s दोनों पक्षों पर शर्तें।
$ $ 0 = T + B \ Rightarrow B = -T $$
स्थानापन्न, A = 1 और B = ,T $ C (s) $ के आंशिक अंश विस्तार में।
$ $ C (s) = \ frac {1} {s} - \ frac {T} {sT + 1} = \ frac {1} {s} - \ frac {T} {T \ left (s + \ frac) 1} {T} \ right)} $ $
$$ \ Rightarrow C (s) = \ frac {1} {s} - \ frac {1} {s + \ frac {1} {T}} $$
व्युत्क्रम लाप्लास परिवर्तन को दोनों तरफ लागू करें।
$ $ c (t) = \ left (1-e ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
unit step response, c (t) में क्षणिक और स्थिर अवस्था दोनों हैं।
इकाई चरण प्रतिक्रिया में क्षणिक शब्द है -
$$ c_ {tr} (t) = - e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
इकाई चरण प्रतिक्रिया में स्थिर स्थिति शब्द है -
$$ c_ {एस एस} (टी) = यू (टी) $$
निम्नलिखित आंकड़ा इकाई चरण प्रतिक्रिया दिखाता है।

का मूल्य unit step response, c(t)t = 0 पर शून्य है और t के सभी नकारात्मक मूल्यों के लिए है। यह धीरे-धीरे शून्य मूल्य से बढ़ रहा है और अंत में स्थिर अवस्था में पहुंचता है। तो, स्थिर स्थिति मान इनपुट के परिमाण पर निर्भर करता है।
फर्स्ट ऑर्डर सिस्टम का रैंप रिस्पांस
इसपर विचार करें unit ramp signal पहले ऑर्डर सिस्टम के इनपुट के रूप में।
$ तो, आर (टी) = टू (टी) $
दोनों तरफ लैपलैस ट्रांसफॉर्म लागू करें।
$$ आर (रों) = \ frac {1} {रों ^ 2} $$
समीकरण पर विचार करें, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
उपर्युक्त समीकरण में स्थानापन्न, $ R (s) = \ frac {1} {s ^ 2} $।
$ $ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 2} \ right) = \ frac {1} {s ^ 2 ( जनजाति +1)} $$
$ C (s) $ के आंशिक अंशों को करें।
$$ सी (रों) = \ frac {1} {रों ^ 2 (एसटी +1)} = \ frac {एक} {रों ^ 2} + \ frac {बी} {s} + \ frac {सी} {जनजाति +1} $$
$$ \ Rightarrow \ frac {1} {s ^ 2 (sT + 1)} = \ frac {A (sT + 1) + Bs (sT + 1) + Cs ^ 2} {s ^ 2 (s + + 1) } $$
दोनों तरफ, हर शब्द समान है। इसलिए, वे एक-दूसरे द्वारा रद्द कर दिए जाएंगे। इसलिए, अंश की शर्तों को समान करें।
$$ 1 = एक (एसटी +1) + बी एस (एसटी +1) + सी ^ 2 $$
दोनों तरफ के स्थिर शब्दों को बराबर करके, आपको A = 1 मिलेगा।
स्थानापन्न, ए = 1 और दोनों पक्षों पर एस शब्दों के गुणांक को समान करें।
$ $ 0 = T + B \ Rightarrow B = -T $$
इसी तरह, बी = andT को प्रतिस्थापित करें और दोनों पक्षों पर $ s ^ 2 $ शब्दों के गुणांक को समान करें। आपको $ C = T ^ 2 $ मिलेगा।
$ C (s) $ के आंशिक अंश विस्तार में A = 1, B = andT और $ C = T ^ 2 $ का स्थान।
$$ सी (रों) = \ frac {1} {रों ^ 2} - \ frac {टी} {s} + \ frac {टी ^ 2} {जनजाति + 1} = \ frac {1} {s ^ 2} -> frac {T} {s} + \ frac {T ^ 2} {T \ left (s + \ frac {1} {T} \ right)} $ $
$$ \ Rightarrow C (s) = \ frac {1} {s ^ 2} - \ frac {T} {s} + \ frac {T} {s + \ frac {1} {T}} $$
व्युत्क्रम लाप्लास परिवर्तन को दोनों तरफ लागू करें।
$ $ c (t) = \ left (t-T + Te ^ {- \ left (\ frac {t} {T} \ right)} \ right) u (t) $$
unit ramp response, c (t) में क्षणिक और स्थिर अवस्था दोनों हैं।
इकाई रैंप प्रतिक्रिया में क्षणिक शब्द है -
$$ c_ {tr} (t) = Te ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
इकाई रैंप प्रतिक्रिया में स्थिर अवस्था शब्द है -
$$ c_ {एस एस} (टी) = (टीटी) यू (टी) $$
निम्नलिखित आंकड़ा इकाई रैंप प्रतिक्रिया दिखाता है।

unit ramp response, c (t) t के सभी सकारात्मक मानों के लिए यूनिट रैम्प इनपुट सिग्नल का अनुसरण करता है। लेकिन, इनपुट संकेत से टी इकाइयों का विचलन होता है।
पहले आदेश प्रणाली के परवलयिक प्रतिक्रिया
इसपर विचार करें unit parabolic signal पहले ऑर्डर सिस्टम के इनपुट के रूप में।
तो, $ r (t) = \ frac {t ^ 2} {2} u (t) $
दोनों तरफ लैपलैस ट्रांसफॉर्म लागू करें।
$$ आर (रों) = \ frac {1} {रों ^ 3} $$
समीकरण पर विचार करें, $ C (s) = \ left (\ frac {1} {sT + 1} \ right) R (s) $
उपर्युक्त समीकरण में $ R (s) = \ frac {1} {s ^ 3} $ का स्थान लें।
$ $ C (s) = \ left (\ frac {1} {sT + 1} \ right) \ left (\ frac {1} {s ^ 3} \ right) = \ frac {1} {s ^ 3 ( जनजाति +1)} $$
$ C (s) $ के आंशिक अंशों को करें।
$$ सी (रों) = \ frac {1} {रों ^ 3 (एसटी +1)} = \ frac {एक} {रों ^ 3} + \ frac {बी} {रों ^ 2} + \ frac {} सी {s} + \ frac {डी} {जनजाति + 1} $$
सरलीकृत करने के बाद, आपको क्रमशः 1, $ -T, \: T ^ 2 \: और \: ^T ^ 3 $ के रूप में ए, बी, सी और डी के मूल्य मिलेंगे। इन मानों को C (s) के आंशिक आंशिक विस्तार में प्रतिस्थापित करें।
$ सी (रों) = \ frac {1} {रों ^ 3} - \ frac {टी} {रों ^ 2} + \ frac {टी ^ 2} {s} - \ frac {टी ^ 3} {जनजाति + 1 } \: \ Rightarrow C (s) = \ frac {1} {s ^ 3} - \ frac {T} {s ^ 2} + \ frac {T ^ 2} {s} - \ frac {T ^ 2} {s + \ frac {1} {टी}} $
व्युत्क्रम लाप्लास परिवर्तन को दोनों तरफ लागू करें।
$ $ c (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2-T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} \ right ) यू (टी) $$
unit parabolic response, c (t) में क्षणिक और स्थिर अवस्था दोनों हैं।
इकाई परवलयिक प्रतिक्रिया में क्षणिक शब्द है
$$ C_ {tr} (t) = - T ^ 2e ^ {- \ left (\ frac {t} {T} \ right)} u (t) $$
इकाई परवलयिक प्रतिक्रिया में स्थिर अवस्था शब्द है
$ $ C_ {ss} (t) = \ left (\ frac {t ^ 2} {2} -Tt + T ^ 2 \ right) u (t) $$
इन प्रतिक्रियाओं से, हम यह निष्कर्ष निकाल सकते हैं कि पहला आदेश नियंत्रण प्रणाली रैंप और पैराबोलिक इनपुट के साथ स्थिर नहीं है क्योंकि ये प्रतिक्रियाएं अनंत समय तक बढ़ती रहती हैं। पहला आदेश नियंत्रण प्रणाली आवेग और चरण इनपुट के साथ स्थिर है क्योंकि इन प्रतिक्रियाओं ने आउटपुट को बाध्य किया है। लेकिन, आवेग प्रतिक्रिया स्थिर अवस्था शब्द नहीं है। इसलिए, चरण संकेतों का उपयोग व्यापक रूप से समय डोमेन में उनकी प्रतिक्रियाओं से नियंत्रण प्रणालियों के विश्लेषण के लिए किया जाता है।