डीएए - मर्ज सॉर्ट
इस अध्याय में, हम मर्ज सॉर्ट पर चर्चा करेंगे और इसकी जटिलता का विश्लेषण करेंगे।
समस्या का विवरण
संख्याओं की सूची को सॉर्ट करने की समस्या खुद को विभाजित करने और जीतने की रणनीति के लिए तुरंत उधार देती है: सूची को दो हिस्सों में विभाजित करें, प्रत्येक आधे को पुन: क्रमबद्ध करें, और फिर दो क्रमबद्ध उप-सूचियों को मर्ज करें।
समाधान
इस एल्गोरिथ्म में, संख्याएँ एक सरणी में संग्रहीत होती हैं numbers[]। यहाँ,p तथा q एक उप-सरणी की शुरुआत और अंत सूचकांक का प्रतिनिधित्व करता है।
Algorithm: Merge-Sort (numbers[], p, r)
if p < r then
q = ⌊(p + r) / 2⌋
Merge-Sort (numbers[], p, q)
Merge-Sort (numbers[], q + 1, r)
Merge (numbers[], p, q, r)Function: Merge (numbers[], p, q, r)
n1 = q – p + 1
n2 = r – q
declare leftnums[1…n1 + 1] and rightnums[1…n2 + 1] temporary arrays
for i = 1 to n1
leftnums[i] = numbers[p + i - 1]
for j = 1 to n2
rightnums[j] = numbers[q+ j]
leftnums[n1 + 1] = ∞
rightnums[n2 + 1] = ∞
i = 1
j = 1
for k = p to r
if leftnums[i] ≤ rightnums[j]
numbers[k] = leftnums[i]
i = i + 1
else
numbers[k] = rightnums[j]
j = j + 1विश्लेषण
आइए हम विचार करें, मर्ज-सॉर्ट का समय चल रहा है T(n)। अत,
$ T (n) = \ start {case} c & if \: n \ leqslant 1 \\ 2 \: x \: T (\ frac {n} {2}) + d \: x \: n & अन्यथा \ अंत {केस} $ जहां c और d स्थिरांक हैं
इसलिए, इस पुनरावृत्ति संबंध का उपयोग करते हुए,
$$ T (n) = 2 ^ i T (\ frac {n} {2 ^ i}) + idn $$
के रूप में, $ i = log \: n, \: T (n) = 2 ^ {log \: n} T (\ frac {n} {2 ^ {log \: n}}) + log \: ndn $
$ = \: cn + dnlog \: n $
इसलिए, $ T (n) = O (n \: log \: n) $
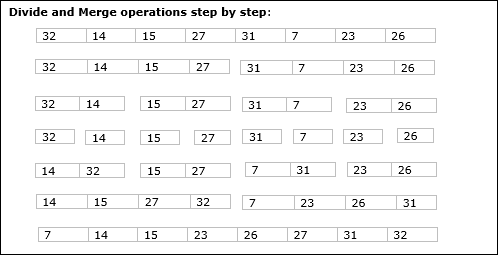
उदाहरण
निम्नलिखित उदाहरण में, हमने मर्ज-सॉर्ट एल्गोरिथ्म को चरण दर चरण दिखाया है। सबसे पहले, प्रत्येक पुनरावृत्ति सरणी को दो उप-सरणियों में विभाजित किया जाता है, जब तक कि उप-सरणी में केवल एक तत्व नहीं होता है। जब इन उप-सरणियों को आगे विभाजित नहीं किया जा सकता है, तो मर्ज संचालन किया जाता है।