DAA - वर्टेक्स कवर

अप्रत्यक्ष ग्राफ का एक शीर्ष-आवरण G = (V, E) कोने का एक सबसेट है V^' ⊆ V ऐसे कि अगर धार (u, v) की एक बढ़त है G, तो कोई u में V या v में V^' अथवा दोनों।

किसी दिए गए अप्रत्यक्ष ग्राफ़ में अधिकतम आकार का एक शीर्ष-आवरण प्राप्त करें। यह इष्टतम वर्टेन्कोवर एनपी-पूर्ण समस्या का अनुकूलन संस्करण है। हालांकि, यह एक शीर्ष-आवरण को खोजने के लिए बहुत कठिन नहीं है जो इष्टतम के पास है।

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

उदाहरण

दिए गए ग्राफ के किनारों का समूह है -

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

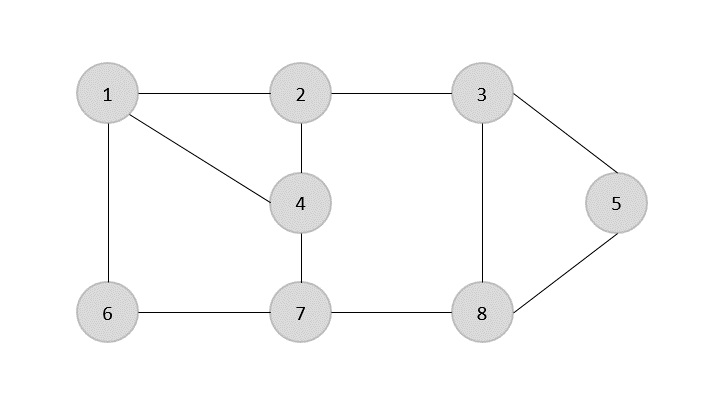
अब, हम एक मनमाना बढ़त (1,6) का चयन करके शुरू करते हैं। हम सभी किनारों को समाप्त कर देते हैं, जो या तो 1 या 6 के शीर्ष पर होते हैं और हम कवर करने के लिए किनारे (1,6) जोड़ते हैं।

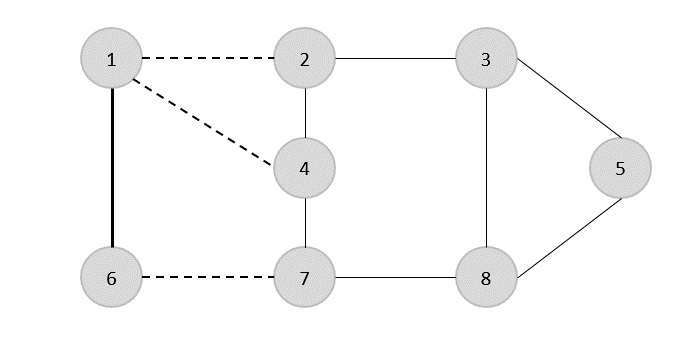
अगले चरण में, हमने यादृच्छिक पर एक और बढ़त (2,3) को चुना है

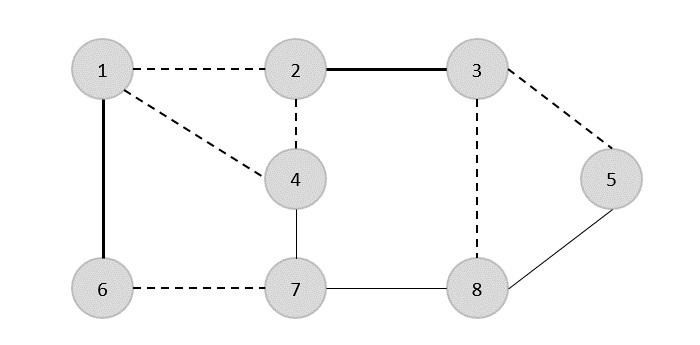
अब हम एक और धार (4,7) का चयन करते हैं।

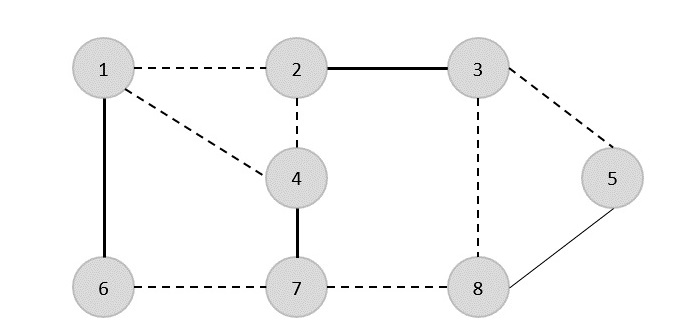
हम एक और धार (8,5) का चयन करते हैं।

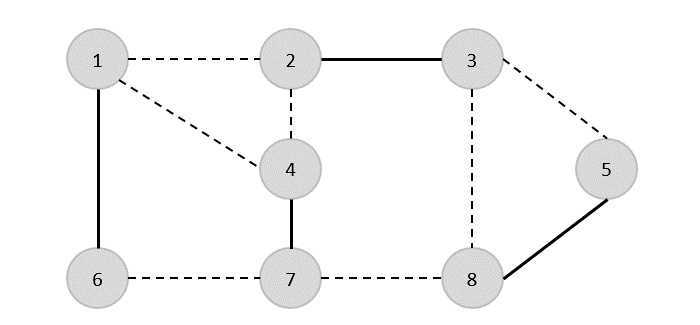
इसलिए, इस ग्राफ का शीर्ष कवर {1,2,4,5} है।

विश्लेषण

यह देखना आसान है कि इस एल्गोरिदम का रनिंग टाइम क्या है O(V + E), प्रतिनिधित्व करने के लिए आसन्न सूची का उपयोग कर E^'।