एनपी हार्ड और एनपी-पूर्ण कक्षाएं

एक समस्या वर्ग एनपीसी में है अगर यह एनपी में है और जैसा है hardएनपी में किसी भी समस्या के रूप में। एक समस्या हैNP-hard अगर एनपी में सभी समस्याएं बहुपद समय के अनुकूल हैं, भले ही वह एनपी में ही न हो।

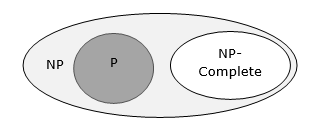
यदि इनमें से किसी भी समस्या के लिए एक बहुपद समय एल्गोरिथ्म मौजूद है, तो एनपी में सभी समस्याएं बहुपद समय हल करने योग्य होंगी। इन समस्याओं को कहा जाता हैNP-complete। एनपी-पूर्णता की घटना सैद्धांतिक और व्यावहारिक दोनों कारणों से महत्वपूर्ण है।

एनपी-पूर्णता की परिभाषा

एक भाषा B है NP-complete अगर यह दो शर्तों को पूरा करता है

B एनपी में है
हर एक A एनपी में बहुपद समय है B।

यदि एक भाषा दूसरी संपत्ति को संतुष्ट करती है, लेकिन जरूरी नहीं कि पहले वाली भाषा ही हो B जाना जाता है NP-Hard। अनौपचारिक रूप से, एक खोज समस्याB है NP-Hard अगर कुछ मौजूद है NP-Complete मुसीबत A कि ट्यूरिंग को कम करता है B।

एनपी-हार्ड में समस्या को बहुपद समय में हल नहीं किया जा सकता है, जब तक P = NP। यदि कोई समस्या एनपीसी साबित होती है, तो इसके लिए एक कुशल एल्गोरिदम खोजने की कोशिश करने में समय बर्बाद करने की आवश्यकता नहीं है। इसके बजाय, हम डिजाइन सन्निकटन एल्गोरिदम पर ध्यान केंद्रित कर सकते हैं।

एनपी-पूर्ण समस्याएं

निम्नलिखित कुछ एनपी-पूर्ण समस्याएं हैं, जिनके लिए कोई बहुपद समय एल्गोरिथ्म ज्ञात नहीं है।

यह निर्धारित करना कि क्या ग्राफ़ में हैमिल्टनियन चक्र है
यह निर्धारित करना कि एक बुलियन सूत्र संतोषजनक है, आदि।

एनपी-हार्ड समस्याएं

एनपी-हार्ड निम्नलिखित समस्याएं हैं

सर्किट-संतोषजनक समस्या
कवर सेट करें
वर्टेक्स कवर
ट्रैवलिंग सेल्समैन की समस्या

इस संदर्भ में, अब हम टीएसपी एनपी-पूर्ण पर चर्चा करेंगे

टीएसपी एनपी-पूर्ण है

यात्रा सेल्समैन समस्या में एक विक्रेता और शहरों का एक सेट शामिल है। सेल्समैन को एक निश्चित शहर से शुरू होने वाले सभी शहरों का दौरा करना होता है और उसी शहर में वापस आना होता है। समस्या की चुनौती यह है कि यात्रा विक्रेता यात्रा की कुल लंबाई को कम करना चाहता है

प्रमाण

साबित करना TSP is NP-Complete, पहले हमें यह साबित करना होगा TSP belongs to NP। टीएसपी में, हम एक दौरा पाते हैं और जांचते हैं कि दौरे में एक बार प्रत्येक शीर्ष शामिल है। फिर दौरे के किनारों की कुल लागत की गणना की जाती है। अंत में, हम जाँचते हैं कि लागत न्यूनतम है या नहीं। यह बहुपद समय में पूरा किया जा सकता है। इस प्रकारTSP belongs to NP।

दूसरी बात, हमें यह साबित करना होगा TSP is NP-hard। यह साबित करने के लिए, एक तरीका यह दिखाना हैHamiltonian cycle ≤_p TSP (जैसा कि हम जानते हैं कि हैमिल्टन चक्र समस्या NPcomplete है)।

मान लीजिये G = (V, E) हैमिल्टन चक्र का एक उदाहरण है।

इसलिए, टीएसपी का एक उदाहरण निर्मित है। हम पूरा ग्राफ बनाते हैंG^' = (V, E^'), कहाँ पे

$ $ E ^ {'} = \ lbrace (i, j) \ colon i, j \ _ V \: \: और \: i \ neq j $$ में

इस प्रकार, लागत समारोह निम्नानुसार परिभाषित किया गया है -

$ $ t (i, j) = \ start {case} 0 & if \: (i, j) \: E \\ 1 में और अन्यथा \ end {केस} $ $

अब, मान लीजिए कि एक हैमिल्टन चक्र h में मौजूद है G। यह स्पष्ट है कि प्रत्येक किनारे की लागतh है 0 में G^' जैसा कि प्रत्येक किनारे का है E। इसलिए,h की लागत है 0 में G^'। इस प्रकार, यदि ग्राफG हैमिल्टनियन चक्र है, फिर ग्राफ G^' का दौरा है 0 लागत।

इसके विपरीत, हम यह मान लेते हैं G^' दौरा है h^' सबसे अधिक लागत की 0। में किनारों की लागतE^' कर रहे हैं 0 तथा 1परिभाषा से। इसलिए, प्रत्येक किनारे की लागत होनी चाहिए0 की लागत के रूप में h^' है 0। इसलिए हम यह निष्कर्ष निकालते हैंh^' केवल किनारों में है E।

हमने इस प्रकार सिद्ध किया है G हैमिल्टनियन चक्र है, यदि और केवल यदि G^' अधिक से अधिक लागत का दौरा किया है 0। टीएसपी एनपी-पूर्ण है।